主成分分析
学习视频:【强烈推荐】清风:数学建模算法、编程和写作培训的视频课程以及Matlab
老师讲得很详细,很受用!!!
定义
主成分分析(PrincipalComponentAnalysis,PCA), 主成分分析是一种降维算法,它能将多个指标转换为少数几 个主成分,这些主成分是原始变量的线性组合,且彼此之间互不相关,其能反映出原始数据的大部分信息。一般来说, 当研究的问题涉及到多变量且变量之间存在很强的相关性时, 我们可考虑使用主成分分析的方法来对数据进行简化。
主成分分析是把原来多个变量划为少数几个综合指标的一种统计分析方法。
降维
降维是将高维度的数据(指标太多)保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度 的目的。 在实际的生产和应用中,降维在一定的信息损失范围内, 可以为我们节省大量的时间和成本。降维也成为应用非常广泛 的数据预处理方法。
降维具有如下一些优点:
- 使得数据集更易使用;
- 降低算法的计算开销;
- 去除噪声;
- 使得结果容易理解。
数学思想

每一行是一个样本,每一列是一个指标。

PCA详细的证明过程可看视频:https://www.bilibili.com/video/av32709936 (证明过程需要一定的多元统计基础和较强的线性代数基础)
计算步骤

标准化目的是消除量纲,归一化目的是便于解释

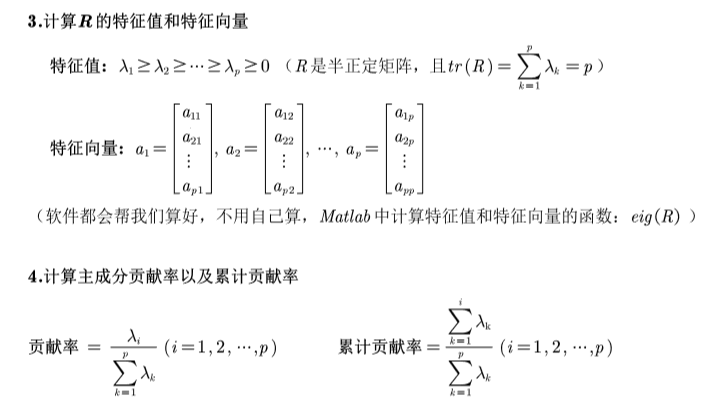

实例分析
问题1
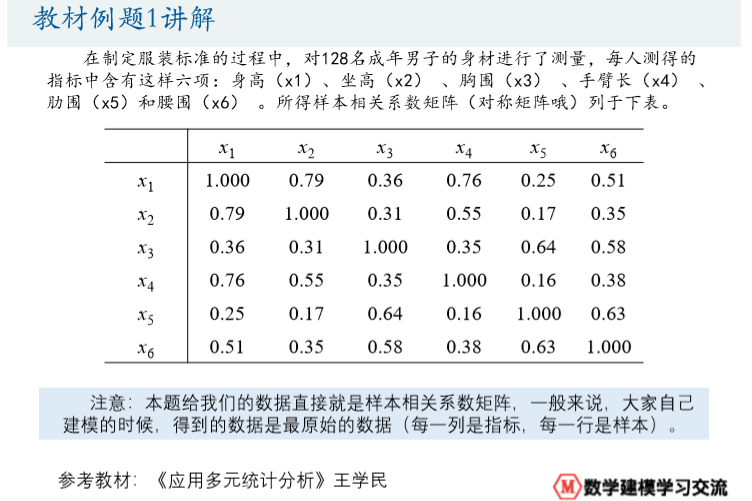
计算关键变量
经过计算,相关系数矩阵的特征值、相应的特征向量以及贡献率列于下表:

从表中可以看到前三个主成分的累计贡献率达85.9%>80.0%,因此可以考虑 只取前面三个主成分,它们能够很好地概括原始变量。
corrcoef函数计算相关系数矩阵。
matlab球的特征值默认归一化。
贡献率的计算是根据特征值/特征值总和计算而来。
写出主成分并简要分析
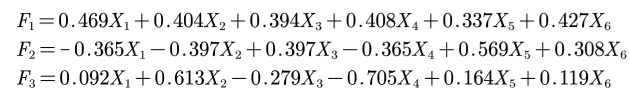
\(X_{i}\)均是标准化后的指标,\(x_{i}\):身高、坐高、胸围、手臂长、肋围和腰围
第一主成分\(F_{1}\)对所有(标准化)原始变量都有近似相等的正载荷,故称第一主成分为(身材)大小成分。
第二主成分\(F_{2}\)及在\(X_{3}, X_{5}, X_{6}\)。上有中等程度的正载荷,而在\(X_{1}, X_{2}, X_{4}\)上有中等程度的负载荷,称第二主成分为形状成分(或胖瘦成分)。
第三主成分\(F_{3}\)在\(X_{2}\)上有大的正载荷,在\(X_{4}\)上有大的负载荷,而在其余变量上的载荷都较小,可称第三主成分为臂长成分。
注:由于第三主成分的贡献率不高(7.65%)且实际意义也不太重要,因此我们也可以考虑只取前两个主成分进行分析。
主成分分析的说明
在主成分分析中,我们首先应保证所提取的前几个主成分的累计贡 献率达到一个较高的水平,其次对这些被提取的主成分必须都能够给出 符合实际背景和意义的解释。
主成分的解释其含义一般多少带有点模糊性,不像原始变量的含义 那么清楚、确切,这是变量降维过程中不得不付出的代价。
因此,提取 的主成分个数m通常应明显小于原始变量个数p(除非p本身较小),否 则维数降低的“利”可能抵不过主成分含义不如原始变量清楚的“弊”。 如果原始变量之间具有较高的相关性,则前面少数几个主成分的累 计贡献率通常就能达到一个较高水平,也就是说,此时的累计贡献率通 常较易得到满足。
主成分分析的困难之处主要在于要能够给出主成分的较好解释,所 提取的主成分中如有一个主成分解释不了,整个主成分分析也就失败了。
主成分分析是变量降维的一种重要、常用的方法,简单的说,该方法要应用得成功,一是靠原始变量的合理选取,二是靠“运气”。
——参考教材:《应用多元统计分析》王学民
问题2
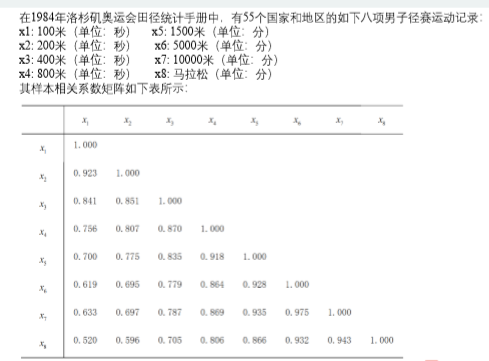
计算关键变量

由上表可知,前两个主成分的累计贡献率已高达93.7%,第一主成分 F1在所有变量上有几乎相等的正载荷,可称为在径赛项目上的强弱成分。 第二主成分F2在各个指标上的载荷基本上逐个递减,反映了速度与耐力成绩的对比。
代码
clear;clc
load data1.mat % 主成分聚类
% load data2.mat % 主成分回归
% 注意,这里可以对数据先进行描述性统计
% 描述性统计的内容见第5讲.相关系数
[n,p] = size(x); % n是样本个数,p是指标个数
%% 第一步:对数据x标准化为X
X=zscore(x); % matlab内置的标准化函数(x-mean(x))/std(x)
%% 第二步:计算样本协方差矩阵
R = cov(X);
%% 注意:以上两步可合并为下面一步:直接计算样本相关系数矩阵
R = corrcoef(x);
disp('样本相关系数矩阵为:')
disp(R)
%% 第三步:计算R的特征值和特征向量
% 注意:R是半正定矩阵,所以其特征值不为负数
% R同时是对称矩阵,Matlab计算对称矩阵时,会将特征值按照从小到大排列哦
% eig函数的详解见第一讲层次分析法的视频
[V,D] = eig(R); % V 特征向量矩阵 D 特征值构成的对角矩阵
%% 第四步:计算主成分贡献率和累计贡献率
lambda = diag(D); % diag函数用于得到一个矩阵的主对角线元素值(返回的是列向量)
lambda = lambda(end:-1:1); % 因为lambda向量是从小大到排序的,我们将其调个头
contribution_rate = lambda / sum(lambda); % 计算贡献率
cum_contribution_rate = cumsum(lambda)/ sum(lambda); % 计算累计贡献率 cumsum是求累加值的函数
disp('特征值为:')
disp(lambda') % 转置为行向量,方便展示
disp('贡献率为:')
disp(contribution_rate')
disp('累计贡献率为:')
disp(cum_contribution_rate')
disp('与特征值对应的特征向量矩阵为:')
% 注意:这里的特征向量要和特征值一一对应,之前特征值相当于颠倒过来了,因此特征向量的各列需要颠倒过来
% rot90函数可以使一个矩阵逆时针旋转90度,然后再转置,就可以实现将矩阵的列颠倒的效果
V=rot90(V)';
disp(V)
%% 计算我们所需要的主成分的值
m =input('请输入需要保存的主成分的个数: ');
F = zeros(n,m); %初始化保存主成分的矩阵(每一列是一个主成分)
for i = 1:m
ai = V(:,i)'; % 将第i个特征向量取出,并转置为行向量
Ai = repmat(ai,n,1); % 将这个行向量重复n次,构成一个n*p的矩阵
F(:, i) = sum(Ai .* X, 2); % 注意,对标准化的数据求了权重后要计算每一行的和
end
%% (1)主成分聚类 : 将主成分指标所在的F矩阵复制到Excel表格,然后再用Spss进行聚类
% 在Excel第一行输入指标名称(F1,F2, ..., Fm)
% 双击Matlab工作区的F,进入变量编辑中,然后复制里面的数据到Excel表格
% 导出数据之后,我们后续的分析就可以在Spss中进行。
%%(2)主成分回归:将x使用主成分得到主成分指标,并将y标准化,接着导出到Excel,然后再使用Stata回归
% Y = zscore(y); % 一定要将y进行标准化哦~
% 在Excel第一行输入指标名称(Y,F1, F2, ..., Fm)
% 分别双击Matlab工作区的Y和F,进入变量编辑中,然后复制里面的数据到Excel表格
% 导出数据之后,我们后续的分析就可以在Stata中进行。
对结果的解释

从上表可以看出,前两个和前三个主成分的累计贡献率分别达到80.6%和 87.8%,第一主成分F1在所有变量(除在x2上的载荷稍偏小外)上都有近似相等的 正载荷,反映了综合消费性支出的水平,因此第一主成分可称为综合消费性支出成分。第二主成分F2在变量x2上有很高的正载荷,在变量x4上有中等的正载 荷,而在其余变量上有负载荷或很小的正载荷。可以认为这个主成分度量了受 地区气候影响的消费性支出(主要是衣着,其次是医疗保健)在所有消费性支出 中占的比重(也可理解为一种消费倾向),第二主成分可称为消费倾向成分。第 三主成分很难给出明显的解释,因此我们只取前面两个主成分。
应用
主成分分析的滥用:主成分得分

除了王老师说的几点原因之外,
补充:
(1)主成分是降维算法,你既然已经有数据了,为什么不把这些数据的信息 全部用上呢?主成分分析是会损失原始数据的信息的。
(2)指标可能有各种类型(极大、极小、区间等),主成分只有标准化的过 程,并没有正向化的过程。
主成分分析用于聚类
计算出第一主成分和第二主成分的值,将其视为两个新的指标 (可以在图上直观的展示各样本的分布情况)。
%% 计算我们所需要的主成分的值
m =input('请输入需要保存的主成分的个数: ');
F = zeros(n,m); %初始化保存主成分的矩阵(每一列是一个主成分)
for i = 1:m
ai = V(:,i)'; % 将第i个特征向量取出,并转置为行向量
Ai = repmat(ai,n,1); % 将这个行向量重复n次,构成一个n*p的矩阵
F(:, i) = sum(Ai .* X, 2); % 注意,对标准化的数据求了权重后要计算每一行的和
end
%% (1)主成分聚类 : 将主成分指标所在的F矩阵复制到Excel表格,然后再用Spss进行聚类
% 在Excel第一行输入指标名称(F1,F2, ..., Fm)
% 双击Matlab工作区的F,进入变量编辑中,然后复制里面的数据到Excel表格
% 导出数据之后,我们后续的分析就可以在Spss中进行。
将主成分指标所在的F矩阵复制到Excel表格,然后再用Spss进行聚类
-
在Excel第一行输入指标名称(F1,F2, ..., Fm)
-
双击Matlab工作区的F,进入变量编辑中,然后复制里面的数据到Excel表格
-
导出数据之后,我们后续的分析就可以在Spss中进行。
结果比较
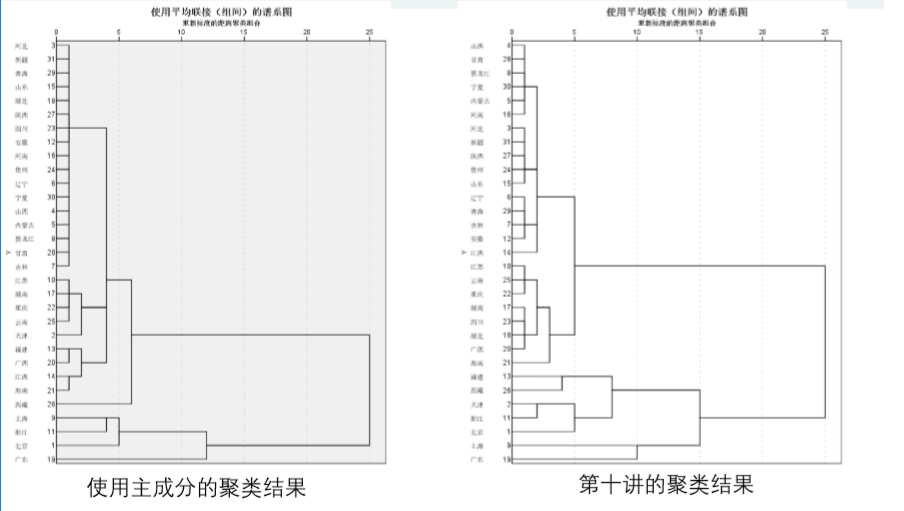
聚类效果图
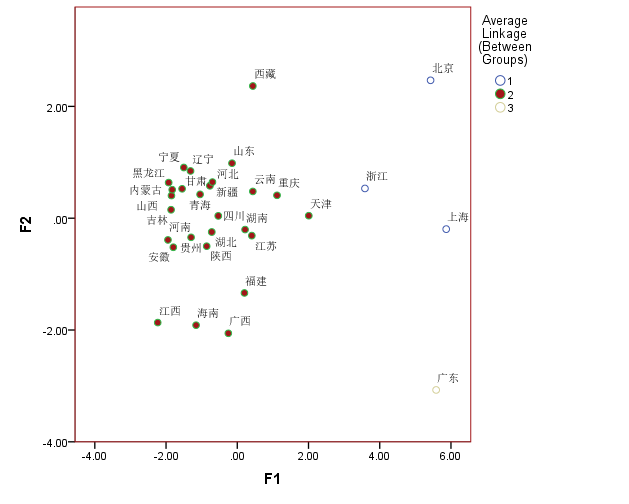
主成分聚类最大的意义就是能帮我们可视化最后的聚类效果,毕竟, 使用主成分是会降低部分信息的。言外之意,只有在指标个数特别多,且指标之间存在很强的相关性时才用主成分聚类。否则会损失很多信息。
主成分回归
主成分回归可用来解决多重共线性的问题。
等我弄完多重共线性问题再补。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号