预测与评价
评价模型
加权平均
一个公式:
Wi = [0.3 0.3 0.2 0.2];%权值
Pi = [95 90 82 85 ;85 95 85 90 ];%单部分评分
P = Wi * Pi'
权值wi难以获得。
层次分析(获取权重)
层次分析:对女星的评价
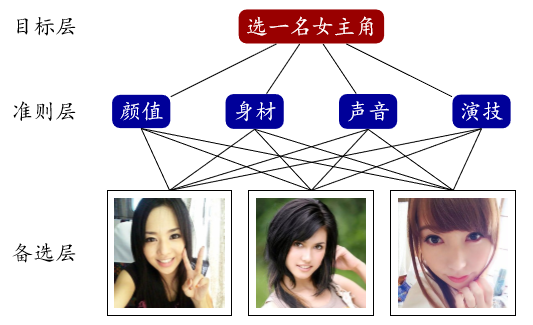
注意可以更多层
层次分析:构造判断矩阵

{1,2,3,...,9}:代表重要程度,逐渐递增
判断矩阵是一个正互反矩阵:
判断矩阵可能会出现矛盾,A>B,B>C,但以后评价C>A,出现不一致,所以需要一致性检验
层次分析:一致性检验
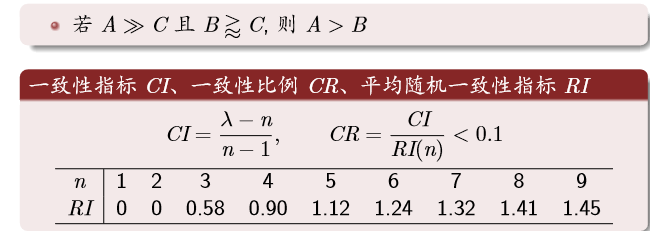
平均随机一致性指标 RI 是确定的
一致性矩阵的定义:
% n= [ 1 2 3 4 5 6 7 8 9
RI = [ 0.00 0.00 0.58 0.90 1.12 1.24 1.32 1.41 1.45];
n = size(A,1);
[V, D] = eig(A);% 计算特征向量V和特征值D: A*V=V*D
[lamda, i] = max(diag(D));% 最大特征值lambda及其位置i
CI=(lamda-n)/(n-1); % 一致性指标
CR = CI/RI(n);% 一致性比例 ,需要小于0.1
层次分析:层次单排序
-
对于上一层某因素而言,本层次各因素的重要性的排序。
-
上一层次某因素相对重要性:判断矩阵 A 对应于最大特征 值 \(λ_{max}\) 的特征向量 W。
A = [1/1 2/1 5/1 3/1 1/2 1/1 3/1 1/2 1/5 1/3 1/1 1/4 1/3 2/1 4/1 1/1]; [w, CR] = AHP(A); function [w, CR] = AHP(A) % n= [ 1 2 3 4 5 6 7 8 9 RI = [ 0.00 0.00 0.58 0.90 1.12 1.24 1.32 1.41 1.45]; n = size(A,1); [V, D] = eig(A);% 计算特征向量V和特征值D: A*V=V*D [lamda, i] = max(diag(D));% 最大特征值lambda及其位置i CI=(lamda-n)/(n-1); % 一致性指标 CR = CI/RI(n);% 一致性比例 ,需要小于0.1 W = V(:,i);% 最大特征值对应的特征向量 w = W/sum(W);% 归一化 例如:[0.48 0.19 0.07 0.26]'
层次分析:层次总排序

在一个因素下,比较各个女明星,得到判断矩阵
% face
A1 = [1/1 1/2 3/1
2/1 1/1 5/1
1/3 1/5 1/1];
[w1, CR1] = AHP(A1);
% body
A2 = [1/1 1/3 2/1
3/1 1/1 5/1
1/2 1/5 1/1];
[w2, CR2] = AHP(A2);
% voice
A3 = [1/1 2/1 1/5
1/2 1/1 1/7
5/1 7/1 1/1];
[w3, CR3] = AHP(A3);
% acting
A4 = [1/1 2/1 1/3
1/2 1/1 1/5
3/1 5/1 1/1];
[w4, CR4] = AHP(A4);
CRs = [CR1 CR2 CR3 CR4]
P = [w1 w2 w3 w4] * w
% ------------------------------------------------------------------------
function [w, CR] = AHP(A)
% n= [ 1 2 3 4 5 6 7 8 9
RI = [ 0.00 0.00 0.58 0.90 1.12 1.24 1.32 1.41 1.45];
n = size(A,1);
[V, D] = eig(A);% 计算特征向量V和特征值D: A*V=V*D
[lamda, i] = max(diag(D));% 最大特征值lambda及其位置i
CI=(lamda-n)/(n-1); % 一致性指标
CR = CI/RI(n);% 一致性比例 ,需要小于0.1
W = V(:,i);% 最大特征值对应的特征向量
w = W/sum(W);% 归一化 例如:[0.48 0.19 0.07 0.26]'
层次分析:总代码
function ahpactor
A = [1/1 2/1 5/1 3/1
1/2 1/1 3/1 1/2
1/5 1/3 1/1 1/4
1/3 2/1 4/1 1/1];
[w, CR] = AHP(A);
% face
A1 = [1/1 1/2 3/1
2/1 1/1 5/1
1/3 1/5 1/1];
[w1, CR1] = AHP(A1);
% body
A2 = [1/1 1/3 2/1
3/1 1/1 5/1
1/2 1/5 1/1];
[w2, CR2] = AHP(A2);
% voice
A3 = [1/1 2/1 1/5
1/2 1/1 1/7
5/1 7/1 1/1];
[w3, CR3] = AHP(A3);
% acting
A4 = [1/1 2/1 1/3
1/2 1/1 1/5
3/1 5/1 1/1];
[w4, CR4] = AHP(A4);
CRs = [CR1 CR2 CR3 CR4]
P = [w1 w2 w3 w4] * w
% ------------------------------------------------------------------------
function [w, CR] = AHP(A)
% n= [ 1 2 3 4 5 6 7 8 9
RI = [ 0.00 0.00 0.58 0.90 1.12 1.24 1.32 1.41 1.45];
n = size(A,1);
[V, D] = eig(A);% 计算特征向量V和特征值D: A*V=V*D
[lamda, i] = max(diag(D));% 最大特征值lambda及其位置i
CI=(lamda-n)/(n-1); % 一致性指标
CR = CI/RI(n);% 一致性比例 ,需要小于0.1
W = V(:,i);% 最大特征值对应的特征向量
w = W/sum(W);% 归一化 例如:[0.48 0.19 0.07 0.26]'
模糊综合评价
- 秃子悖论: 天下所有的人都是秃子
-
设头发的根数为 n,n = 1 显然为秃子。
-
若 n = k 为秃子,则 n = k+ 1 亦为秃子。
- 模糊概念
-
从属于该概念到不属于该概念之间无明显分界线。
-
用隶属程度代替属或不属于,如某人属于秃子的程度为 0.8。
- 模糊综合评价要素
- 因素集:U =
- 评语集:V = {超棒v1, 很棒v2, 不错v3, 一般v4, 呕心v5
- 权重 W 和网友投票 (%) R
权重 W来自:层次分析或者权威数据

苍井的第一行例子为:
颜值:38%的网友认为超棒,34%的网友认为很棒,......
-
模糊合成

代码实现:
W = [0.4 0.2 0.1 0.3]; R = [0.38 0.34 0.17 0.11 0.00 0.26 0.41 0.20 0.13 0.00 0.27 0.23 0.21 0.15 0.14 0.14 0.19 0.22 0.12 0.33]; % B = max(R .* W')%新版 B = max(R .* repmat(W',1,size(R,2)) ) %repmat 平铺结果说明:
B=[B1,B2,B3,B4,B5],
根据评语集:V = {超棒v1, 很棒v2, 不错v3, 一般v4, 呕心v5}
如果B2最大,则说明很棒v2,如果B3最大,则说明不错v3。
预测模型
拟合
拟合是最基本的预测方法。
MATALB函数:polyfit / fit 。
时间序列
定义
时间序列:将预测对象按照时间顺序排列而成的序列。
时序预测:根据时序过去的变化规律,推测今后趋势。
时间序列的变化形式
-
长期趋势变动 Tt
-
季节变动 St
-
循环变动 Ct
-
不规则变动 Rt
模型
-
加法模型 (\(Tt+St+Ct+Rt\))
-
乘法模型 (\(Tt*St*Ct*Rt\))
-
混合模型
移动平均法

有前几个月的收入,预测下一个月的收入,具体取前面N的月的值取一下平均即可。适用波动不大的数据。
% 近9月企业的收入,求第10月收入
y = [533.8 574.6 606.9 649.8 705.1, ...
772.0 816.4 892.7 963.9 ];
m = length(y);
n = 4;% 最好去波动的周期
c = cumsum(y);%前缀和
yhat = ( c(n:end)-[0 c(1:end-n)] )/n;
%[(y1+...+y4) - 0, (y1+...+y5) - y1, (y1+...+y6) - (y1+y2)]/n
%[cn-0,c(n+1)-c(1),c(n+2)-c(2)........]/n
yhat
S = norm(yhat(1:end-1) - y(n+1:end))/sqrt(m-n)
平滑法

灰色预测
特点
- 模型使用的不是原始数据,而是生成数据。
- 不需要很多数据,一般只需 ≥ 4 个数据。
- 只适用于中短期的预测,只适合指数增长的预测。
GM(1,1) 预测模型
GM(1,1) 表示模型是 1 阶微分方程,且只含 1 个变量。
步骤如图:




代码
t0 = [1999:2003]';
X0 = [89, 99, 109, 120, 135]';% 原始序列
n = length(X0);
lambda = X0(1:n-1)./X0(2:n);%可行性检验条件
range = minmax(lambda') % 检验
exp([-2/(n+1), 2/(n+2)])
X1 = cumsum(X0); % 累加生成序列
Z1 = (X1(1:n-1)+X1(2:n))/2 % 均值
B = [-Z1, ones(n-1,1)];
Y = X0(2:n);
u = B\Y; a = u(1); b = u(2);% 最小二乘估计a,b
k = 0:n+4;
xhat1 = (X0(1) - b/a).*exp(-a*k) + b/a;
xhat0 = [X0(1) diff(xhat1)] % 还原
plot(t0,X0,'o',t0(1)+k, xhat0,'-+')