【Luogu1217】[USACO1.5]数字三角形（数塔问题） ——动态规划基础

markdown好像炸了 不管了懒得改能看懂就行233

算了吧良心一点改好了

有形如图所示的数塔，从顶部出发，在每一结点可以选择向左走或是向右走，一起走到底层，要求找出一条路径，使路径上的值最大。

请无视CSDN的水印

要求输出最大和

接下来，我们来分析一下解题思路：

用二维数组来存放数字三角形

我们用\(D(r,j)\)来表示第\(r\) 行第\(j\)个数字(\(r,j\)从\(1\)开始算)

我们用\(f(r,j)\)表示从\(D(r,j)\)到底边的各条路径中，最佳路径的数字之和。

因此，此题的最终问题就变成了求\(f(1,1)\)

\(D(r,j)\)出发，下一步只能走\(D(r+1,j)\)或者\(D(r+1,j+1)\)。故对于\(N\)行的三角形，我们可以写出如下的递归式：

if(r==N)                
	f(r,j)=D(r,j)  
else      
	f(r,j)=max{f(r+1,j),f(r+1,j+1)}+D(r,j) 

然而很明显递归不是正解 会超时。因为我们对同一点重复递归了多次，时间复杂度\(O(n^2)\)。

很容易想到记忆化递归。

代码：

#include <iostream>  
#include <algorithm> 
using namespace std;
#define MAX 101
int D[MAX][MAX],n,f[MAX][MAX];
int work(int i,int j){      
	if(f[i][j])
		return f[i][j];
	if(i==n)
		f[i][j]=D[i][j];
	else{
		int x=work(i+1,j);       
		int y=work(i+1,j+1);       
		f[i][j]=max(x,y)+D[i][j];     
	}     
	return f[i][j]; 
} 
int main(){    
	int i,j;    
	cin>>n;    
	for(i=1;i<=n;i++)   
		for(j=1;j<=i;j++) {       
			cin>>D[i][j];       
			f[i][j]=-1;   
		}    
	cout<<work(1,1)<<endl;
	return 0;
} 

$ AC $撒花！

——————————————————分割线————————————————————

另一种做法就是爆搜啦！

当然要用记忆化搜索。

这里不再赘述。

——————————————————分割线————————————————————

我们并不能满足于这样的代码，因为递归总是需要使用大量堆栈上的空间，很容易造成栈溢出，我们现在就要考虑如何把递归转换为递推。

我们首先需要计算的是最后一行，因此可以把最后一行直接写出，如下图：

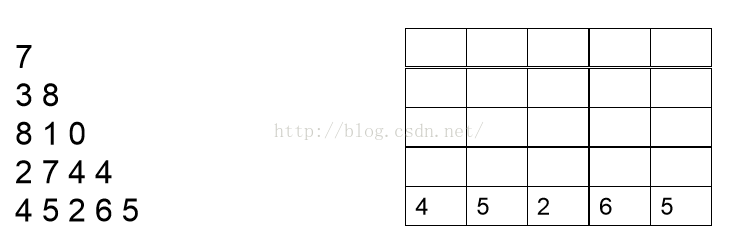
现在开始分析倒数第二行的每一个数，现分析数字2，2可以和最后一行4相加，也可以和最后一行的5相加，但是很显然和5相加要更大一点，结果为7，我们此时就可以将7保存起来，然后分析数字7，7可以和最后一行的5相加，也可以和最后一行的2相加，很显然和5相加更大，结果为12，因此我们将12保存起来。以此类推。我们可以得到下面这张图：

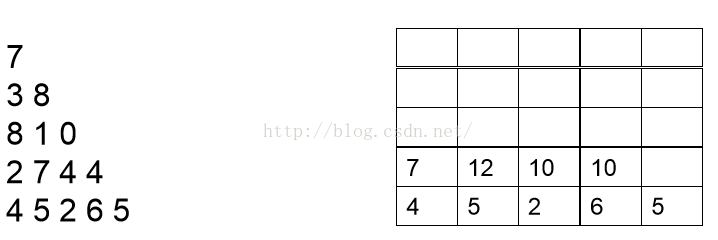
然后按同样的道理分析倒数第三行和倒数第四行，最后分析第一行，我们可以依次得到如下结果：

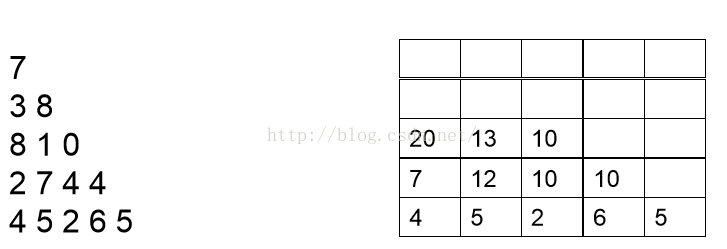
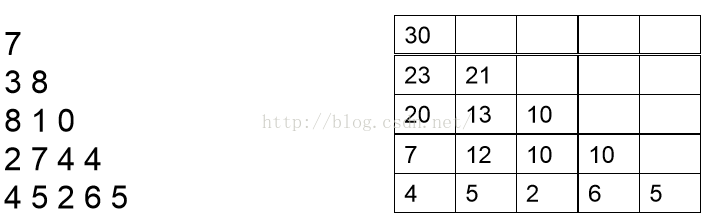
容易写出代码

#include<iostream>
using namespace std;
int n, d[100][100];
int main(){
	cin>>n;
	for(int i=1; i<=n; i++)
		for(int j=1; j<=i; j++)
			cin>>d[i][j];
	for(int i=n-1; i>0; i--)
		for(int j=1; j<=i; j++)
			d[i][j]=d[i][j]+max(d[i+1][j], d[i+1][j+1]);
	cout<<"max="<<d[1][1]<<endl;
	return 0;
}

我们仍然可以继续优化，而这个优化当然是对于空间进行优化，其实完全没必要用二维数组存储每一个\(f(r,j)\),只要从底层一行行向上递推，那么只要一维数组\(d[100]\)即可,即只要存储一行的值就可以。

一维数组优化：

#include<iostream>  
using namespace std; 
#define MAX 101  
int d[MAX][MAX],n,* f; 
int main(){    
	int i,j;    
	cin>>n;    
	for(i=1;i<=n;i++)   
		for(j=1;j<=i;j++)        
			cin>>d[i][j];
	f=d[n];//f是指针 等价于数组
	for(i=n-1;i>=1;i--)     
		for(j=1;j<=i;j++)       
			f[j]=max(f[j],f[j+1])+d[i][j];    
	cout<<f[1];
        return 0;
}

$ AC $撒花！

部分内容及图片来自教你彻底学会动态规划——入门篇