OpenGL中坐标系的理解（一）
在OpenGL中，存在着至少存在着三种矩阵，对应着函数glMatrixMode()的三个参数：GL_MODELVIEW，GL_PROJECTION，GL_TEXTURE。
以下主要描述GL_MODELVIEW（模型视图矩阵）的个人理解。
在OpenGL中空间中点的三维坐标是使用行向量表示的，虽然与列向量相比存储结构并没有发生变化，但在坐标变换（即矩阵乘法）中会有很大不同。大家都知道一个4X4的矩阵可以表示三维坐标的平移，旋转变换。例如一矩阵R表示一个旋转加平移变换，空间中一点P(x, y, z)，如果坐标使用列向量表示，则变换过程为
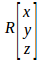
如果坐标使用行向量表示，则变换过程为上述矩阵的转置
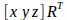
因此，OpenGL中变换矩阵采用的是右乘的方式，并且其需要的变换矩阵其实是真正变换矩阵的转置（前提是矩阵在数组中采取的是以行为主的形式，即先存储完矩阵的一行，接下来再存储矩阵的下一行）。
函数glLoadMatrixf(const GLfloat *m)输入的矩阵其实是变换矩阵R的转置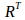
。
如果先后对空间中一点P(x, y, z)作多次变换，设先后的变换矩阵分别为A，B，C，则在OpenGL中应当如何输入变换矩阵呢？当坐标使用列向量表示时，变换过程为
当坐标使用行向量表示时，变换过程为
因此，OpenGL中，最先变换的矩阵应当最后与当前矩阵相乘，并且乘的是变换矩阵的转置。下面我以一个例子来说明上述变换。注意下面描述中的x，y，z轴实际上指的是相机坐标系中的U，V，N轴。OpenGL中，屏幕中所呈现的视平面其实是UOV平面，屏幕上方为V轴正方向，屏幕右方为U轴正方向，屏幕由里到外为N轴正方向。因此视线方向总是沿N轴负方向。
函数rotate(float angle, float x, float y, float z)是让坐标点绕向量(x, y, z)旋转angle角度，旋转方向符合右手螺旋定则。函数translate(float x, float y, float z)是让坐标点沿向量(x, y, z)平移其模长的距离。上述两个函数生成的都是变换矩阵的转置，并且实现的都是
，其中M是当前矩阵，R是变换矩阵。
1 matrixView.identity(); //transform matrixView to an identity 2 matrixView.translate(0, 0, -r); 3 glLoadMatrixf(matrixView.get());
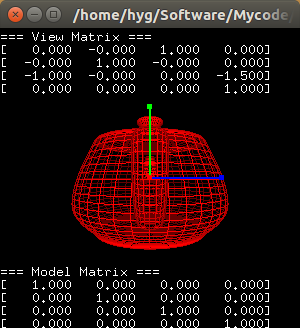
上述矩阵是由一个单位阵加沿负N轴的平移转换而成，假设在世界坐标系中有一茶壶，其中心位于世界坐标系的原点，在上述变换矩阵下如下图：
图中，红，绿，蓝箭头分别为世界坐标系的x，y，z轴。下面是让该茶壶先后沿x，y，z轴旋转90度的代码和结果截图
1 matrixView.identity(); //transform matrixView to an identity 2 matrixView.rotate(90, 1, 0, 0); //cameraAngleX 3 matrixView.translate(0, 0, -r); 4 glLoadMatrixf(matrixView.get());
1 matrixView.identity(); //transform matrixView to an identity 2 matrixView.rotate(90, 1, 0, 0); //cameraAngleX 3 matrixView.rotate(90, 0, 1, 0); //cameraAngleY 4 matrixView.translate(0, 0, -r); 5 glLoadMatrixf(matrixView.get());
1 matrixView.identity(); //transform matrixView to an identity 2 matrixView.rotate(90, 1, 0, 0); //cameraAngleX 3 matrixView.rotate(90, 0, 1, 0); //cameraAngleY 4 matrixView.rotate(90, 0, 0, 1); //cameraAngleZ 5 matrixView.translate(0, 0, -r); 6 glLoadMatrixf(matrixView.get());
