P9369

whk 选手做思维题保持手感 /kel

还是好题，思路整体挺顺畅。

力求严密些。

---

题意：给定一棵树，定义一个集合是好的当且仅当其满足两点条件中任意一点：

• $\forall u, v \in S$，$u \in \text{subtree}(v)$ 或 $v \in \text{subtree}(u)$。
• $\forall u, v \in S$，$u \not\in \text{subtree}(v)$ 且 $v \not\in \text{subtree}(u)$。

求最小的 $k$，使得可以将树上所有节点不重不漏划分至 $k$ 个好集合中。

---

其实不重没什么用，显然好集合的子集也是好集合。

为方便叙述，将根到某点的路径上的点的集合称为一条链，将满足第一个条件的集合称为 A 型集合，将满足第二个条件的集合称为 B 型集合。

B 型集合的条件很奇怪。所以先研究 A 型集合，找到最优解的一个性质，再来处理 B 型集合。

1. 存在最优解的形式形如：有 $m$ 个点（后称为黑点），每个 A 集合是根到其中一个点的路径。

容易发现 A 型集合是一条链的子集。设链的另一端为 $u$。容易发现将根到 $u$ 上整条路径都放进同一集合不劣。

2. 若所有链上白点数目的最大值为 $t$，则再取 $t$ 个 B 集合可以覆盖所有白点。

同链上的点不能属于一个 B 型集合，这就说明了这是下限。

考虑在树上 dfs 的过程，这里增量构造。

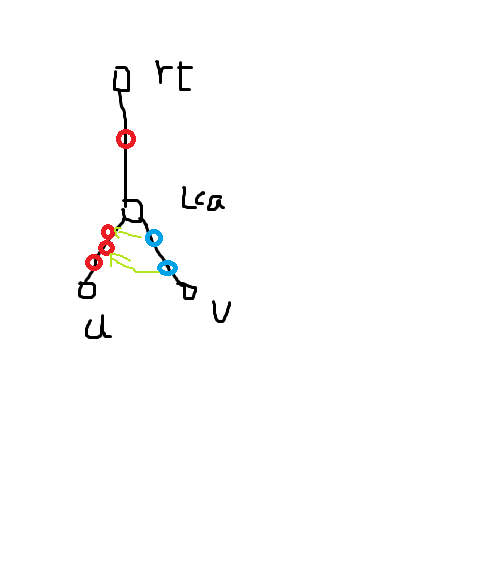
只考虑 dfs 时访问的叶结点（一个点处的要求包含其父亲），则一条链上的白点是从其另一端点起的连续的一段路径。忽略掉 lca 处已经被处理过的点，从上到下将 未处理的点合并到 $u$ 链上的点。这样显然不会使用超过 $t$ 个集合。

本质是，点 $u$ 所在集合的编号是【它的祖先中离它最近的的白点】所在集合的编号加一。可以归纳证其合法性。

枚举几个 B 型集合就行了。那么关键是找到黑点数目的最小值。

3. 设一个点到其子树中叶结点的距离的最大值为 $mx_u$，则若 B 型集合有 $k$ 个，最小化黑点时，黑点恰为所有 $mx=k$ 的点。

若 $mx_u > k$，这个点不该被染黑，因为黑点的子树中不能有黑点。

若 $mx_u < k$，改而将其父亲染黑不劣。

一个点的父亲的 $mx$ 大于它本身的 $mx$，于是存在最优解只使用所有 $mx=k$ 的点，此时必须取全所有 $mx=k$ 的点，故结论得证。

做完了。

一个月没写代码的人一遍写对，很感动。

#include <bits/stdc++.h>
const int M = 1e6 + 5;

void solve() {
  int n; scanf("%d", &n);
  std::vector<int> fa(n + 1), mx(n + 1), cnt(n + 1);
  for (int i = 2; i <= n; i++) 
    scanf("%d", &fa[i]);
  for (int i = n; i >= 1; i--) {
    mx[fa[i]] = std::max(mx[fa[i]], mx[i] + 1);
    ++cnt[mx[i]];
  }
  int ans = n;
  for (int i = 0; i <= n; i++)
    ans = std::min(ans, cnt[i] + i);
  printf("%d\n", ans);
}

int main() {
  int T; scanf("%d", &T); while (T--) {
    solve();
  }
  return 0;
}