群论小记

定义#

群：一个集合 $G$，和一个定义在其元素上的二元运算，这里记为 $*$。

群需要满足的性质：

• 封闭性：$\forall a, b \in G, a * b \in G$
• 单位元：$\exist e \in G, \forall a \in G, a * e = a$
• 逆元：$\forall a \in G, \exist b \in G, a * b = b * a = e$，将这里的 $b$ 记作 $a^{-1}$
• 结合律：$(a * b) * c = a * (b * c)$

例子：膜 $m$ 的完系与加法、膜 $p$ 的缩系和乘法。

一个很好的视角是把 $G$ 中的元素看成某种操作，此时 $*$ 可以描述操作的复合。

后面一般不区分 $G$ 与 $*$ 构成的群，和集合 $G$。

现在来研究一个集合 $S$ 和一个群 $G$，$G$ 中的元素 $g:S \to S$ 是一个映射，把 $s$ 经过映射 $g$ 后的结果记为 $g \cdot s$。对于 $g_1, g_2 \in G$，$g_1 * g_2$ 为先经过 $g_1$ 再经过 $g_2$ 后得到的映射。通常的计数问题要研究 $S$ 经过 $G$ 中的所有变换后可能出现的本质不同的等价类的个数。

可以将一个元素 $s \in S$ 同时看成一个变换，此时可以忽略 $S$ 集合，直接研究 $G$ 中所有变换在复合操作下的等价性。在 $S$ 中取 $s$ 使得 $f(g) = g \cdot s$ 是一个 $G$ 到 $S$ 的双射，将 $s_1 = g \cdot s$ 替换成 $g \cdot s$，则这个视角下的操作与原来的操作是等价的。

例如说，$S$ 为膜 $n$ 完系，$G$ 为【加上 $0$ 到 $n-1$ 中的任意一个数】与操作复合构成的群（幺元为【加零】）。此时【$x$】与【在【$0$】上施加【加 $x$】】等价。 将 $S$ 中的元素【$x$】看作 $G$ 中的元素【加上 $x$】，即可忽略集合 $S$。

（上两段话曾经卡住了我一阵子，非常感谢 [官方双语]欧拉公式与初等群论_哔哩哔哩_bilibili 提供的视角）

一个具体的例子是，$S$ 是【给一个正 $n$ 边形的各顶点染两种颜色的方案的集合】，$G$ 为【所有可能的旋转方案】。【旋转 $a$ 次】与【旋转 $b$ 次】复合等价于【旋转 $(a + b) \bmod n$ 次】，显然逆元存在，故 $G$ 是群。容易发现 $|S| = 2^n, |G| = n$。当 $n=4$ 时，【$(0, 1, 1, 0)$】 通过【旋转 $2$ 次】操作得到【$(1, 0, 0, 1)$】，故上述两种染法隶属于同一等价类。

值得点出的是，因为 $G$ 是一个群，$\forall g_1, g_2 \in G, g_1 * g_2 \in G$。

注意：$(g_1 * g_2) \cdot s = g_2 \cdot (g_1 * s)$。群的定义中没有交换律，有交换律的是阿贝尔群。

定义：记 $s$ 的轨 $G(s)$ 为：$\{g \cdot s \mid g \in G\}$。容易发现 $G(s) \subseteq S$。

一个轨恰好构成一个等价类看似很直观，但之后将给予代数证明。故所求仅轨的种类。

容易发现，对于固定的 $g_x \in G, f_{g_x}(g) = g * g_x$ 事实上是一个双射。证明由幺元唯一性显然。幺元唯一性由反证法显然。

轨的性质#

• 性质一：若 $G(a) \cap G(b) \neq \varnothing, G(a) = G(b)$。

  由对称性只用证 $G(a) \subseteq G(b)$。

  设 $t \in G(a) \cap G(b), g_1 \cdot a = t, g_2 \cdot b = t$，则 $\forall c \in G(a),g_3 \cdot a = c, (g_2 * g_1^{-1} * g_3) \cdot b = c$，即 $c$ 在 $b$ 的轨中。

• 性质二：对于 $b, c \in G(a), \exist g \in G, g \cdot b = c$。

  设 $g_1 \cdot a = b, g_2 \cdot a = c$，则 $(g_1^{-1} * g_2) \cdot b = c$。

• 推论：若 $G(s) = \{s_1, s_2, \dots, s_k\}$，则 $G(s_1) = G(s_2) = \ldots=G(s_k)$。

• 定义：对 $s \in S$，定义 $s$ 的稳定子群 $G_s$ 为 $\{g \mid g \cdot s = s, g \in G\}$ 与 $*$ 构成的代数系统。容易发现 $G_s \subseteq G$。

• 性质三：$e \in G_s$。

• 性质四：$g \in G_s \Rightarrow g^{-1} \in G_s$。

  $g^{-1} \cdot s = g^{-1} \cdot (g \cdot s) = (g^{-1} * g) \cdot s = s$。

• 性质五：$g_1, g_2 \in G_s \Rightarrow g_1 * g_2 \in G_s$。

  $(g_1 * g_2) \cdot s = g_1 \cdot s = s$。

由 $G$ 的交换律知 $G_s$ 也有交换律，故 $G_s$ 也是群。

• 定义：若 $G$ 是一个群，$G_1 \subseteq G$ 且由 $G_1$ 关于 $*$ 封闭，则称 $G_1$ 为 $G$ 的子群。

• 性质六：若 $G_1$ 是 $G$ 的子群，则 $\dfrac{|G|}{|G_1|} \in \mathbb Z$。

  实例：$G$ 为【乘上膜 $p$ 缩系中的一个数】，直接研究 $G$ 中所有变换在复合意义下的等价性，则所有【乘上一个二次剩余】构成一个稳定子群。证明由欧拉准则得出。熟知二次剩余的个数是 $\dfrac{p-1}{2}$。

  • 定义：在群 $G$ 上定义左陪集 $h*G := \{h * g \mid g \in G\}$。陪集不一定是群。

  • 引理：若 $G_1$ 是 $G$ 的子群，则 $G$ 可划分为若干个不交的 $G_1$ 的左陪集。

    仅考虑 $|G_1| \neq |G|$ 的非平凡情况。

    • 设 $g * G_1 = G_2$，则 $G_1$ 与 $G_2$ 相等或不交。

      若 $g \in G_1, G_2 = G_1$。否则，若存在 $r \in G_1 \cap G_2$，设 $g * g_1 = r, g_1 \in G_1$，则 $g = r * g_1^{-1} \in G_1$，矛盾。

    以此方式写出所有左陪集 $G_1, G_2,\dots, G_n$。

    • $G$ 中任意元素均在某左陪集中出现

      任取 $g_x \in G$，$g_x = (g_x * g_1^{-1}) * g_1$，在 $g_x * g_1^{-1}$ 的左陪集中。

    • 若 $G_2 \cap G_3 \neq \varnothing$，$G_2 = G_3$。
      

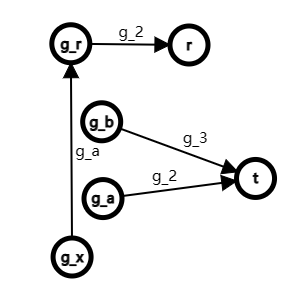
      $a \stackrel{c}\longrightarrow b$ 的意义为 $c * a = b$。它体现了封闭性这一性质。结合律无法在这张图上体现。

      如图，$g_r, g_a, g_b$ 均为 $G_1$ 中的元素，$g_2 G = G_2$ 为第二个左陪集，$g_3 G = G_3$ 为第三个左陪集。$t \in G_2 \cap G_3$，其余定义见图。

      对于任取的 $r \in G_2$，只需证明 $r \in G_3$，则有 $G_2 \subseteq G_3$，由对称性可知 $G_3 \subseteq G_2$，则得证。

      容易注意到 $r = g_2 * g_r = g_2 * g_a * g_x = t * g_x = g_3 * g_b * g_x$，显然 $g_b * g_x \in G$，故 $r \in g_3 G$。

    引理得证。

  由引理，将 $G$ 写作 $g_1 G \cup g_2 G \cup \cdots g_kG$，必须有 $|g_1G| = |g_2G| = \cdots = |g_kG|$（可以将 $g_2G$ 看作 $G_1$ 中每个元素左复合某个 $g \in G$ 构成的集合，每个由复合生成的元素各不相等），故 $\dfrac{G}{G_1} = k \in \Z$。

• 定义：若 $G_1$ 为 $G$ 的子群，称 $\dfrac{G}{G_1}$ 为 $G_1$ 在 $G$ 中的指数，记作 $[G : G_1]$，数值上等于 $G_1$ 所有左（右）陪集的个数。

• （拉格朗日定理）$\forall s \in S, [G:G_s] = |G(s)|$。（$|G_s| |G(s)| = n$，轨大小乘稳定子群大小等于群大小）

  令 $G_s$ 为上一定理证明中的 $G_1$，容易发现对于同一个 $G_i$ 中的 $g_a, g_b$，$g_a \cdot s = g_b \cdot s$（证明由以 $G_s$ 中任一元素操作 $s$ 结果相同容易推出）；对于不同 $G_i$ 中的 $g_a, g_b$，$g_a \cdot s \neq g_b \cdot s$（将上述过程倒过来容易反证），故得证。

• 可以由拉格朗日定理推出伯氏引理（Burnside 引理），证明可由算两次给出，OI-wiki 上有证明，但是其直接使用了拉格朗日定理。懒了，到此为止 /youl

写在最后#

根据 lcx 讲的一节课以及自己在 b 站看的一些科普视频整理而成，前后时间跨度极大，不少群本身的性质没有细证。不过写完后挺理性愉悦的，还顺带学了一些 $\LaTeX$ 的用法，太酷啦。

迈向抽象代数的临门一脚。