决策单调性笔记

题单

给定 \(w_{i,j}\)，对 \(i \in [1,n]\) 求 \(f_{i} = \min_{j=1}^{i-1} \{w_{j,i} + f_j\}\)。

我们需要研究对于怎样的 \(w_{j,i}\) 能获得怎样的优化

二分队列 & 二分栈

参考资料：https://www.cnblogs.com/flashhu/p/9521094.html

把 \(f_j + w_{j,i}\) 看成关于 \(i\) 的函数，那么每次我们要加入一个函数、查询某点处函数极值。

如果能保证任意两个函数至多一个交点，可以直接维护凸壳（事实上这时连接两个点的不一定是直线但一定是某个函数的一段），维护连续两个点横坐标与连接它们的函数的标号。这个似乎被叫做二分队列，斜率优化可以完全被它取代。

如果能保证 \(i \to \infty\) 时新插入函数最优，则可以直接在最右边插入新函数，不断弹出不够优的函数（一定是一段后缀）。查询点递增可以直接挪左端点，否则可以二分之。复杂度均摊是 \(O(n \cdot \omega(n))\) 或 \(O(n \log n \cdot \omega(n))\)（询问点无序），\(\omega(n)\) 是找到两函数交点的时间复杂度。容易发现插入直线时是漂亮的 \(O(n)\)，与斜率优化的复杂度一致，而且非常自然、可拓展化，不局限于直线。

如果能保证 \(i\) 最小时新插入函数最优，则直接用单调栈，最左插入最左删除。可以是斜率递增求 \(\max\) 之类长远看来越早插入越优的东西。

总结下来，任意两个函数应当至多有一个交点，一个新函数应当与凸包最多两个交点，而应用中的插入函数类型一致（二次函数、根号函数、一次函数）。如果 \(i\) 取到极值时新插入函数最优，则新插入函数应当只交凸包一次，找到那个交点来重构凸包，复杂度均摊 \(O(\omega(n))\)，询问可以选择挪指针或二分。否则要在中间插入，只能平衡树维护（同样重构凸包）或 CDQ 分治维护（好写不少，强制中序转移，对询问点的性质无要求）。

斜率（询问点）单调暴力移指针

斜率不单调二分找答案

x坐标单调开单调队列

x坐标不单调开平衡树 | cdq分治

P5504 插入的是二次函数，斜率递增且求 \(\max\)，队尾插入决策队尾删除，用的是栈。

CF1067D 插入的是直线但求的点值要到 \(10^{18}\) 的范围，所以要二分交点

P3515 插入的是二分之一次函数。

以上建立在函数容易求交点或单点求值的基础上，如果无法轻易单点求值，就需要另辟蹊径。

分治

参考资料：https://www.luogu.com.cn/blog/command-block/dp-di-jue-ce-dan-diao-xing-you-hua-zong-jie

二分栈中，凸包本身的存在，插入时弹出前缀或后缀（部分题目）可证明了决策单调性。

分治的基础是同层 dp 之间互不干涉，这样才能打乱同层 dp 数组计算的顺序。

考虑每次算出区间的决策点后递归，用莫队维护 \(w_{i,j}\)。分治 \(\log\) 层，每层左右端点移动和 \(O(n)\)，故总复杂度 \(O(n \log n \omega(n))\)，最后一项是移动指针的复杂度。

int calc(int l, int r) {
    while(R < r) add(a[++R]);
    while(L > l) add(a[--L]);
    while(R > r) subt(a[R--]);
    while(L < l) subt(a[L++]);
    return ans;
}
void solve(int l, int r, int sl, int sr) {
    if(l > r || sl > sr) return;
    int mid = l + r >> 1, pl = 0;
    for(int i = sl; i <= sr; i++) {
        if(i > mid) continue;
        int tmp = g[i-1] + calc(i, mid);
        if(f[mid] > tmp) f[mid] = tmp, pl = i;
    }
    solve(l, mid-1, sl, pl); solve(mid+1, r, pl, sr);
}

分治的前提是函数各层互不干预且区间信息容易用莫队维护。容易在增加和删除时统计对答案贡献变化值的信息是方便用莫队维护的。

CF868F 的区间颜色相同对数，P5574 的区间逆序对数，CF833B 的区间颜色数，都是方便用此种方法维护的信息。

需要决策单调性，不需要四边形不等式。存在这种东西。

四边形不等式

图源 https://www.luogu.com.cn/blog/command-block/dp-di-jue-ce-dan-diao-xing-you-hua-zong-jie

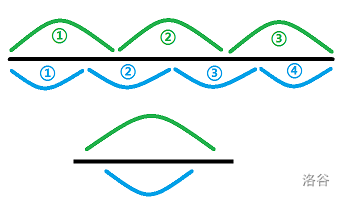
若 \(w_{p1,p3} + w_{p2,p4}\) 与 \(w_{p1,p4} + w_{p2,p3}\) 的不等关系一定（交叉优于包含），则 \(w\) 满足四边形不等式。此时 \(f\) 具有决策单调性。

反而感觉上面那张图是最好的证明。

设 \(g_{i,j}\) 是 \(i\) 数分 \(j\) 段的决策点，此时会有 \(g_{i,j-1} \leq g_{i,j} \leq g_{i+1,j}\)，这保证了求出一层所有转移点的复杂度是 \(O(n)\) 的。总复杂度就是 \(O(n(n+k))\)，如果做 \(k\) 次。但是要求信息能快速求出。 可以移指针做。

for j : 1 to k
  for i : n to 1
    for p : opt(i, j - 1) to opt(i + 1, j)
      if [f(p, j - 1) < f(i, j)] opt(i, j) = p, f(i, j) := f(p, j - 1) ; 

来源

也可以按 \(j-i\) 转移，差不多。

CF833B 的权值是区间颜色数，另一个方法是用线段树维护决策，移动右指针时更新决策。这个方法基于移动右端点时能贡献到的区间的左端点是一个集合，复杂度与分治做法一致故可以只考虑分治。

CF321E 的权值是一段二维前缀和，可以用此方法维护做到 \(O(n^2)\)，\(n,k\) 同阶。当然也能分治做，但是分治没有最大利用方便求值的性质，能做到 \(O(n^2 \log n)\)。

咕。