P8046 [COCI2015-2016#4] CHEWBACCA 题解

发现自己的思路与那篇题解不同，而且可以跑更大的数据，所以来写个题解。

题意：给定一棵满 \(k\) 叉树，树的节点同层从左往右编号，深度较小的节点的编号一定小于深度较大的节点的编号，多次询问两点距离。

先思考 \(k=2\) 的情况。

我们知道，一个节点的左儿子就是它的编号乘二，右儿子的编号就是它的编号乘二加一，父亲的编号是它的编号除二向下取整。这个除二向下取整是个好性质，保证了倍增向上跳时能快速找到 \(2^m\) 级祖先。

现在看 \(k=3\) 的情况。

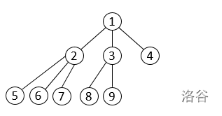
\(2\) 的儿子是 \(5,6,7\)，而我们希望这是 \(6,7,8\)。

如何推广 \(k=2\) 呢？注意到 \(i\) 层的节点刚好是 \(2\) 进制下有 \(i\) 位的所有数从大到小的排列，首先我们需要前 \(i\) 层共 \(k^i-1\) 个节点。

考虑一个这样第 \(i\) 层有 \((k-1) \cdot k^{i-1}\) 个节点的图

这个图相当于把原树复制了 \(k-2\) 遍并重新编号。

前 \(i\) 层共 \(k^i-1\) 个节点，满足我们推广的需要。

这样 \(i\) 层刚好从 \((10\cdots0)_k\)（\(i\) 个 \(0\)） 开始编号，最后一位的 \(k\) 个数刚好对应同一个父亲，我们要的编号除以 \(k\) 是父亲性质也满足了。

怎么找到一个节点的新编号呢？先找到它在第几层，然后把它的编号加上那 \(k-2\) 棵树前 \(i-1\) 层节点个数之和即可。

这样的好处是我们可以倍增跳节点了，可以把数据限制从 \(n\) 改为 \(d\)，\(d\) 为深度。

不过既然深度是 \(\log\) 级别的，估计改到那时就要 \(k\) 进制输入了吧 /xyx

反正树不高，我的实现仍是暴力向上跳。

#include <cstdio>
#include <iostream>
#include <algorithm>
#define LL long long
using namespace std;
const int M = 50;
LL n, k; int q; LL sum1[M], sum2[M], sum[M], step[M], num[M];
int getdep(LL x){ // 原编号算深度
    for(int i = 1; i <= 30; i++) {
		if(sum[i-1] >= x) return i;
	}
    return 0;
}
int dep(LL x){ // 新编号算深度
	for(int i = 1; i <= 30; i++){
		if(sum2[i] >= x) return i;
	} return 0;
}
LL solve(LL x, LL y){
    if(k == 1) return max(x, y) - min(x, y);
    int depx = getdep(x), depy = getdep(y), ans = 0;
    if(x != 1) x += (k-2) * sum[depx - 2];
    if(y != 1) y += (k-2) * sum[depy - 2];
    // 此时得到新的 x 与 y，后面看另一篇题解就够了
    while(x != y){
    	if(x < y) swap(x, y);
    	x /= k; ++ans;
	}
	return ans;
}
int main(){
    scanf("%lld %lld %d", &n, &k, &q);
    sum[0] = num[0] = 1ll; step[0] = k;
    for(int i = 1; i <= 30; i++)
        num[i] = num[i-1] * 2, step[i] = step[i-1] * k, sum[i] = sum[i-1] + step[i-1];
    sum2[1] = k-1;
    for(int i = 1; i <= 30; i++)
    	sum2[i] = sum2[i-1] * k;
    while(q--){
        LL x, y;
        scanf("%lld %lld", &x, &y);
        printf("%lld\n", solve(x, y));
    }
}