P7676 [COCI2013-2014#5] TROKUTI 题解

这题最多评绿吧……

发现自己的做法和那篇题解不同，所以来发个题解。

题意：给定 \(n\) 条直线，求这些直线两两交出的三角的个数。保证无三线共点。

明显任意三条不平行的直线能确定一个三角。所以有一个做法是先算全部再排除选了两条或三条斜率相同线的情况。然而这篇题解讲的并不是这个做法，而是另一个我先想到的做法。

观察样例解释，

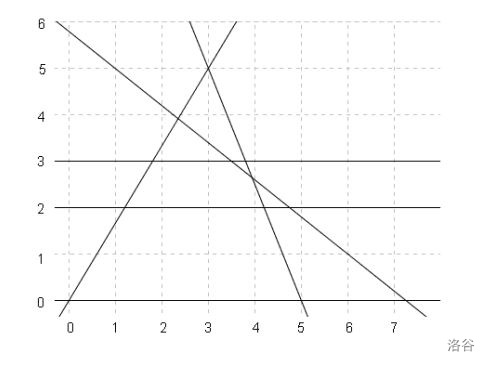
有三条平行直线，可不可以当做一条看待呢？

两条能与 \(y=3\) 交出三角的直线，必然也能与 \(y=2\) 交出三角。分配律一下，即可把两条直线合到一起。

这样的话，相当于给每条直线一个权值，表示有几条线与它斜率一致。每次选三条直线相乘，贡献三条直线权值之积。

约分给定斜率，用 map 判重，然后一遍背包，即可。

#include <cstdio>
#include <map>
#include <algorithm>
using namespace std;
const int M = 300005, mod = 1000000007;
int n, a[M], b[M], c[M], h[M], cnt, dp[M][4];
map<pair<int, int> , int> t1; map<pair<int, int> , bool> t2;
pair<int, int> k[M];
int main(){
    scanf("%d", &n);
    for(int i = 1; i <= n; i++){
        scanf("%d %d %d", &a[i], &b[i], &c[i]);
        int g = __gcd(a[i], b[i]); k[i] = make_pair(a[i]/g, b[i]/g);
        if(k[i].first < 0) k[i].first = -k[i].first, k[i].second = -k[i].second;
        t1[k[i]]++;
    }
    for(int i = 1; i <= n; i++) {
        if(!t2[k[i]]) h[++cnt] = t1[k[i]]; t2[k[i]] = 1;
    }
    dp[0][0] = 1; 
    for(int i = 1; i <= cnt; i++){
        dp[i][0] = dp[i-1][0];
        for(int j = 1; j <= 3; j++){
            dp[i][j] = (1ll * dp[i-1][j-1] * h[i] % mod + dp[i-1][j]) % mod;
        }
    }
    printf("%d\n", dp[cnt][3]);
}