LCT 学习笔记

看看学弟们几天后会把 LCT 给卷了：cntnow = 0

LCT 好难啊呜呜呜

这 LCT，尤其是 makeroot 中的区间翻转一步，根本不是人想到的。

~~虽然 Splay 也不是人想到的。~~

写了一些忽然发现网上有写的很好的了，那就这样，图直接放人家的，主要用来~~存代码~~方便背代码（

再写这样的对话几次后干脆给这两人取个正式点的名字吧（突发奇想

引入

A：让我们开始吧。从问题引入：在线维护一个森林，有连边、断边、查询两点路径的操作。如果这是一个静态问题，你会怎么操作？

B：无断边加边，这就是树剖模板。

A：为什么要用树剖呢？

B：往上跳时若当前非其重儿子，即换了一条链，子树大小至少*2，保证任意点到根至多换log条链。链的存储连续，这让我们可以用其它数据结构维护序列。

A：我们是怎么把树剖开的呢？

B：通过人工挑选“重儿子”

A：开始引入第一对概念：“实儿子”与“虚儿子”。每个节点都有唯一的“实儿子”。这样，树就被剖分成若干链了。用什么维护链比较好呢？

B：既然上链还动态了，当然用平衡树了！

辅助树

A：来介绍 LCT 的核心 - 辅助树。

之前说过，我们使用 Splay 分别维护树上每条链

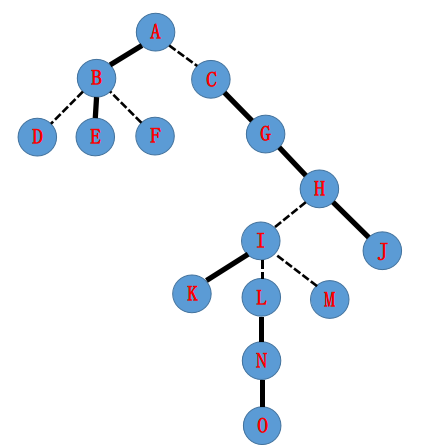
（图源：https://www.cnblogs.com/flashhu/p/8324551.html，后面还会引这里的图）

剖好后长后面这个样。

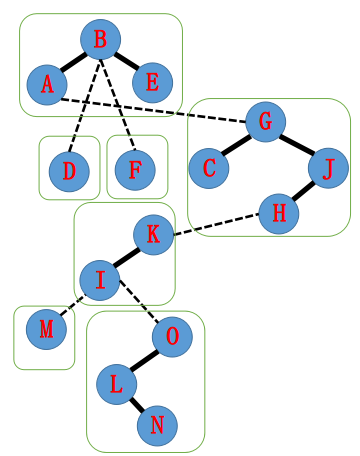
这棵树有些可爱的小性质，参照第一张图上的轻重链看。

B：

每条重链构成一棵 Splay，中序遍历后在原树对应从上到下那条链。
每棵 Splay 的根节点的根连向该链最上部的节点原树上的父亲
通过辅助树能唯一还原原树那么为了保持树的形状，我们要让到其它儿子的边变为虚边，由对应儿子所属的Splay的根节点的父亲指向该点，而从该点并不能直接访问该儿子（认父不认子）。

A：最后一条告诉我们不用管原树，就管改辅助树。该上操作了。

为了保持树的形状，我们要让到其它儿子的边变为虚边，由对应儿子所属的Splay的根节点的父亲指向该点，而从该点并不能直接访问该儿子（认父不认子）。

警告&声明

在以后的阅读请分清操作在原树还是在辅助树上。虽然我们只操作辅助树，很多时候会叙述这对原树的宏观影响。

“断***”相当于把这条边由实边变为虚边。

Splay 相关数组声明与宏定义

A：既然与 Splay 相关，直接看代码吧。

#define ls(x) ch[x][0]
#define rs(x) ch[x][1]
#define isroot(x) (ch[fa[x]][0] != x && ch[fa[x]][1] != x)
int sz[M], rt, tot, fa[M], ch[M][2], val[M], cnt[M];
void pushup(int x) {sz[x] = sz[ls(x)] + sz[rs(x)] + cnt[x];}
bool get(int x) {return x == rs(fa[x]);}

pushup：字面意思

isroot：是否是辅助树中所在 Splay 的根

get：是 fa 的哪边儿子

特殊的 rotate

A：记得 rotate 吗……

因为认父不认子，我们需要对 rotate 做改造。

old version

void rotate(int x){ 
	int y = fa[x], z = fa[y], chk = get(x);
	ch[y][chk] = ch[x][chk ^ 1]; if(ch[x][chk ^ 1]) fa[ch[x][chk ^ 1]] = y; //处理 x 另一方向的儿子 
	fa[y] = x; ch[x][chk ^ 1] = y; fa[x] = z; //yx 父子关系对调 
	if(z) ch[z][y == ch[z][1]] = x; //xz 连边 
	pushup(y); pushup(x); 
}
void splay(int x, int goal){ //使 x 为 goal 儿子 
	while(fa[x] != goal){ //相当于判 x 是否到达
		int y = fa[x], z = fa[y];
		if(z != goal) //相当于判 y 是否到达
            rotate(get(x) == get(y) ? y : x);
		rotate(x);
	} if(!goal) rt = x;
}

z 是 x 的父亲的父亲。y 实际上不是 x 的父亲的可能可以排除，因为在外部的 splay 中会有检查。现在只需看 z 实际上是不是 x 的父亲。

void rotate(int x){ 
	pushdown(fa[x]); pushdown(x);
	int y = fa[x], z = fa[y], chk = get(x);
    if (!isroot(y)) ch[z][ch[z][1] == y] = x; //特殊的 xz 连边
	ch[y][chk] = ch[x][chk ^ 1]; if(ch[x][chk ^ 1]) fa[ch[x][chk ^ 1]] = y; //处理x另一方向的儿子 
	fa[y] = x; ch[x][chk ^ 1] = y; fa[x] = z; //yx父子关系对调 
	pushup(y); pushup(x); 
}
void update(int x){
	if(!isroot(x)) update(fa[x]);
	pushdown(x);
}
void splay(int x){ //使 x 为所在 Splay 的根 
	while(!isroot(x)){ //所有 fa[x] == goal 均应改为 isroot(x)
		int y = fa[x];
		if(!isroot(y)) rotate(get(x) == get(y) ? y : x);
		rotate(x);
	}
}

access

A：access 用于构建一条原树上树根到给定点的实路径。

现在假设我们要让 root 到 N 构成实链。

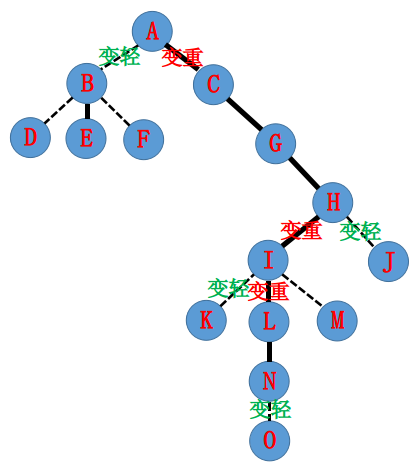
提示：从下到上。

B：第一步把 NO 间的边变轻。在辅助树上，只需让 O 成为 N 的直系儿子，然后让 N 不认 O，即可。因为 N 在辅助树上的 Splay 上仅在 N 后面，这可以通过 Splay(N) 实现。

A：下一步，需要断掉 IK 间的实边，因为一个节点只能有一个实儿子。

B：Splay(I) 后，K 就会成为 I 的右儿子。想要精准操控两个在原树中有父子关系的节点，只需要把其中一个转至所在 Splay 的根，另一个节点一定与其成辅助树上的父子关系。

此时递归下去即可。注意到上一段实际上是在构造 K 到根的路径，做下去即可。

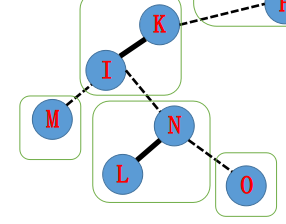
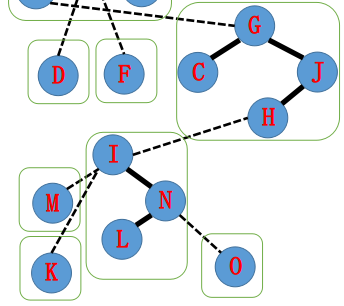
总结：旋转到所在 Splay 的根，断右子树，把新的右子树连为转移来的节点，更新信息，转移到当前节点的 fa 做下去。

void access(int x){ //构建 x 到根的路径
    int f = x;
    for(int y = 0; x; y = x, x = fa[x]){
        splay(x); ch[x][1] = y; pushup(x);
    }
    splay(f); // 最好把 x Splay 到根 —— U 群神的指示
}

makeroot

A：有时候，我们需要直接处理树上两点间的路径。找到 LCA 肯定不是最佳方法，我们希望这两个点能构成祖孙关系。

B：让其中一点成为原树上的根，另一点自然是它的晚辈。

A：所以，我们需要让 x 成为原树上深度最小的节点。这怎么做呢？

B：Splay 可以区间翻转，翻转过的区间的相对位置不变，如果翻转一条链呢？

A：问题不大。只有存储在这条链上的信息会改变，其它链的信息不会变，也就是所有链的父亲也不会变，对于它们来说，拓扑结构也不会变。只是对于翻转的那条链原来的父亲来说会有点麻烦。有什么好方法避免吗？

B：只要翻转的链含有根节点，就一切解决了。所有链的父亲节点不变，拓扑结构不变。一遍翻转后，原来最下面的节点事实上成为了新根。

access x 后把 x 旋到根，翻转所在 Splay，即可。

A：那就可以上代码了：

void makeroot(int x){
	access(x); splay(x); 
	laz[x] ^= 1; swap(ch[x][0], ch[x][1]); //打懒标记交换左右子树
}

副作用：构建 x 到原根的路径。

findroot

A：为了判断连通性，我们有时需要查找一个点在原树上的树根。

B：access 恰好为我们打通了这个点到树根的路径。然后查找所在 Splay 的最左节点返回即可。

A：是的。这里可以直接上代码：

int findroot(int x){
	access(x); splay(x);
	int y = x;
	while(ls(y)) pushdown(y), y = ls(y);
	return splay(y), y; //保证 splay 复杂度
}

为了保证 Splay 复杂度，查找到的点要 Splay 到根。

副作用：打通了这个点到根的路径，并且最后 splay 的根是原树的根。

split

A：其实有了 access 和 findroot 后一切都很简单了。

split(x, y) 表示把 x 到 y 的路径拆出来维护。

makeroot x 后 access y 再 splay y 即可把 x 到 y 之间路径上的节点集中到以 y 为根的 Splay。

为什么 access 后经常 splay？因为访问 Splay 需要借助根，不知道根很难访问。

void split(int x, int y){
	makeroot(x); access(y); splay(y);
}

副作用：换根为 x，x 与 y 在一个 Splay，x 与 y 的路径均在以 y 为根的 Splay 里。

link

A：带一句即可。

字面意思。

B：把 x 和 y 旋到对应 Splay 的根节点然后让 x 做 y 父亲即可。

bool link(int x, int y){//造出的 splay 以 y 为根
	makeroot(x); if(findroot(y) == x) return 0;
	fa[x] = y; return 1;
}

连的是虚边，所以不用 pushup x。

cut

A：先来个判定。

B：x 与 y 之间有边等价于 makeroot x 并 access y 并 splay y 后 x 与 y 直接相连。因为 x 是根，splay 后 x 必须是 y 的左儿子。同时，x 与 y 之间不能有其它点，即 x 不能有右儿子。

让 x 不认 y 即可。

因为直接改了 Splay 的结构，这次要 pushup y 了。pushup 后，为了更新信息，最好 splay 一下。

附：

其实不 splay 不会错，查询时会 splay，顺便更新标记了。

但还是觉得 link/cut 后顺手 splay 好，一方面据说多旋旋可以保证复杂度，一方面顺便更新信息。虽然不更新不会错但我就是强迫症（

bool cut(int x, int y){
	makeroot(x); access(y); splay(y);
	if(fa[x] != y || rs(x)) return 0;
	ls(y) = fa[x] = 0; pushup(y); splay(y); return 1;
}

完整代码

//time : 2022-06-18
//problem url : https://www.luogu.com.cn/problem/P3690
//status : AC
#include <cstdio>
#include <queue>
#define ONLINE_JUDGE
#ifndef ONLINE_JUDGE
#define dprintf printf
#define debug() printf("fa:"); for(int i = 1; i <= n; i++) printf("%d ", T.fa[i]); printf("\n");\
printf("sons:"); for(int i = 1; i <= n; i++) printf("%d-%d ", T.ls(i), T.rs(i)); printf("\n");\
printf("vals:"); for(int i = 1; i <= n; i++) printf("%d-%d ", T.val[i], T.s[i]); printf("\n");
#define debug1() printf("fa:"); for(int i = 1; i <= n; i++) printf("%d ", fa[i]); printf("\n");\
printf("sons:"); for(int i = 1; i <= n; i++) printf("%d-%d ", ls(i), rs(i)); printf("\n");\
printf("vals:"); for(int i = 1; i <= n; i++) printf("%d-%d-%d ", val[i], s[i], laz[i]); printf("\n");
#else
#define debug() 
#define debug1()
#define dprintf
#endif
#define inf 10000005
using namespace std;
const int M = 100005;
int read(){
	int x = 0, f = 1; char c = getchar();
	while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();}
	while(c >= '0' && c <= '9') {x = x * 10 + c - '0'; c = getchar();}
	return x * f;
}
void write(int x){
	if(x < 0) {putchar('-'); x = -x;}
	if(x > 9) write(x / 10);
	putchar(x % 10 + '0');
	return;
}
int op, x, n, m, y, a[M];
struct LCT{
	#define ls(x) ch[x][0]
	#define rs(x) ch[x][1]
    #define isroot(x) (ch[fa[x]][0] != x && ch[fa[x]][1] != x)
	int sz[M], rt, tot, fa[M], ch[M][2], val[M], cnt[M], laz[M], s[M];
	void pushup(int x) {sz[x] = sz[ls(x)] + sz[rs(x)] + cnt[x]; s[x] = (s[ls(x)] ^ s[rs(x)] ^ val[x]);}
	void put(int x) {laz[x] ^= 1; swap(ls(x), rs(x));}
	void pushdown(int x) {if(!laz[x]) return; put(ls(x)); put(rs(x)); laz[x] = 0;}
	bool get(int x) {return x == rs(fa[x]);}
	void clear(int x) {ch[x][0] = ch[x][1] = fa[x] = val[x] = sz[x] = cnt[x] = 0;}
	int build(int x) {sz[++tot] = 1; cnt[tot] = 1; s[tot] = val[tot] = x; return tot;}
	void rotate(int x){ 
		pushdown(fa[x]); pushdown(x);
		int y = fa[x], z = fa[y], chk = get(x);
        if (!isroot(y)) ch[z][ch[z][1] == y] = x; //特殊的 xz 连边
		ch[y][chk] = ch[x][chk ^ 1]; if(ch[x][chk ^ 1]) fa[ch[x][chk ^ 1]] = y; //处理x另一方向的儿子 
		fa[y] = x; ch[x][chk ^ 1] = y; fa[x] = z; //yx父子关系对调 
		pushup(y); pushup(x); 
	}
	void update(int x){
		if(!isroot(x)) update(fa[x]);
		pushdown(x);
	}
	void splay(int x){//使 x 所在子树的根 
		update(x);
		while(!isroot(x)){
			int y = fa[x];
			if(!isroot(y)) rotate(get(x) == get(y) ? y : x);
			rotate(x);
		}
	}
	void access(int x){//构建 x 到根的路径
        int f = x;
        for(int y = 0; x; y = x, x = fa[x]){
			// dprintf("y=%d x=%d\n", y, x);
            splay(x); rs(x) = y; pushup(x);
			debug1()
        }
        splay(f);
    }
	void makeroot(int x){//让 x 成为原树的根
		access(x); splay(x); put(x);
	}
	int findroot(int x){ //操作完后 splay 的根是原树上的根
		access(x); splay(x);
		int y = x;
		while(ls(y)) pushdown(y), y = ls(y);
		return splay(y), y; //保证 splay 复杂度
	}
	void split(int x, int y){
		makeroot(x); access(y); splay(y); 
	}
	bool link(int x, int y){//造出的 splay 以 y 为根
		makeroot(x); if(findroot(y) == x) return 0;
		fa[x] = y; return 1;
	}
	bool cut(int x, int y){
		makeroot(x); access(y); splay(y);
		if(fa[x] != y || rs(x)) return 0;
		ls(y) = fa[x] = 0; pushup(y); splay(y); return 1;
	}
	void modify(int x, int y){
		splay(x); val[x] = y; pushup(x);
	}
}T;
int main(){
	scanf("%d %d", &n, &m);
	for(int i = 1; i <= n; i++) T.build(read());
	while(m--){
		scanf("%d %d %d", &op, &x, &y);
		if(op == 0) T.split(x, y), printf("%d\n", T.s[y]);
		else if(op == 1) T.link(x, y);
		else if(op == 2) T.cut(x, y);
		else T.modify(x, y);
		debug()
	}
}

I LOVE LCT FOREVER!

LCT 真是神仙才能想到的东西。

发现学弟评论了 LCT 第一篇题解，他们卷 LCT 的时间也近了吧 /bx

posted @ 2022-06-18 13:24 purplevine 阅读(46) 评论(0) 编辑收藏举报

刷新页面返回顶部

Loading

purplevine

LCT 学习笔记

LCT 学习笔记

引入

辅助树

警告&声明

Splay 相关数组声明与宏定义

特殊的 rotate

access

makeroot

findroot

split

link

cut

完整代码

I LOVE LCT FOREVER!

公告