后缀数组学习笔记

莫反是越学越难，SA 只会越学越简单。 ——谭老师

说在最前 ：等学完 SAM 后我会继续更的。现在先写些对于 SA 和后缀树的理解。

于开头 % 一下 ZHY 的 AC 自动机笔记 & LZY 的 AC 自动机笔记

进入正题吧。

据说对话式的文章用于重现思路很方便，那就来试试。

仅重思路，不重某些特别具体的推导。

---

为什么我们需要后缀？

A：后缀这玩意，有什么用，是什么人在处理什么恶心的问题时头脑一热想到的？

B：先说字符串吧。

字符串，长度长，值域小，所以可以拿来干很多事，如自我匹配（回文串、重复串等等），与别的串匹配（公共串等等），关键是对子串进行处理。

数据结构的思路是节省算力，利用已知简化求未知。一个字符串的所有子串的数量是什么级别呢？

A：\(O(n^2)\)。

B：那么，维护什么数量级小于这个的东西，也可以在 \(O(1)\) 或很小的时间内描述一个子串呢？

A：子串有一个 \(l\) 和一个 \(r\)，我想到了，是前缀和！

B：不错。

A：那为什么一定是后缀数组不是前缀数组呢？

B：你问发明人去……？

怎么处理后缀呢？

A：那知道了为什么我们需要后缀，我们应该如何处理后缀，才能让它保留我们需要的信息呢？

B：嗯……子串是后缀的前缀，与从头开始的连续的字符相关的数据结构，你能想到什么呢？

A：Trie！从头开始，就是从根插入。

B：让我们来看一棵用后缀集合构成的字典树——后缀树。

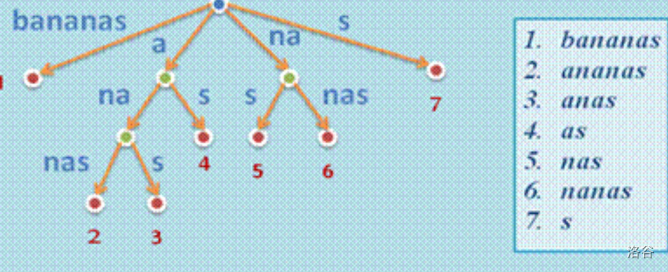
为了节省空间，这是一棵经过压缩的字典树。

A：怎么构建呢？

B：我们晚点再说吧。（我也不会，所以是真 · 晚点）

注：一般在字符最后插入特别字符（如 美元符号 以保证所有后缀的结尾均为叶结点，那张图没有画出来）

后缀树的性质 & 后缀数组的引入

B：字典树的空间复杂度与结点数和字符集相关。观察一下这棵后缀树，它的结点的数量级是多少呢？

A：每次插入仅最多增加两个结点，它的数量是 \(O(n)\) 的。

B：我们之前说过，这些关键结点与从头开始的连续的字符相关，这有什么特别含义吗？

A：每个叶结点是一个后缀的结尾，从头开始的连续的结点，就是后缀的前缀，也就是子串。

B：来做道题吧。如何求出一个字符串的最长重复子串？

A：只要找从根到非叶结点路径的最长值就行了。从叶回溯即能遍历所有可能成为答案的结点。

B：如何判断一个串是否是给定字符串的子串？你当然可以用 KMP \(O(n)\) 求。

A：直接从根往下找，同 Trie。

B：给定串在原字符串中出现次数呢？当然，这也能用 KMP 求。

A：从根往下找到它之后，看有多少叶结点是它的子节点。

B：不错。总结下来，从根节点到某个结点的路径，对应了一个子串。 我们是怎么做到仅使用 \(O(n)\) 的空间的呢？

A：我们只保留了所有叶结点的 LCA，就像一棵虚树那样。

B：好。不妨假设子节点有序，即字典序。此时的叶结点也是有序的了。这序号有什么含义呢？

A：就是对后缀的排序。

B：LCA 有一种类似“归并”的性质（此时请思考一下 Tarjan 离线 LCA），借助后缀排序，我们也可以有一个更好的方法来处理 LCA，也就是一个公共子串了。

后缀数组的求法

B：为了维护这些子串，你要维护什么信息呢？

A：嗯……首先要知道排好序的数组的那个顺序。可以维护 sa[] 和 rk[] 两个数组，前者表示“排行 i 的后缀的起始点在哪里”，后者表示“起始点为 i 的后缀排行第几”，为了研究 LCA，还需要相邻两个叶结点的 LCA 相关信息，即 \(sa_i\) 与 \(sa_{i+1}\) 的最长公共前缀（Least Common Prefix，LCP）。

B：好，我们先求前面两个数组。有什么暴力思路吗？

A：直接把所有子串丢入 sort，\(O(n^2 \log n)\)。如果用字符串 Hash 配合二分，可以优化到 \(O(n \log^2 n)\)。

B：想想看，我们的瓶颈在哪里？

A：这些字符串本身是有关系的，而上面的两个解法，都没有利用这个关系。

B：字符串是可以合并的——

A：我们使用倍增，即可合并地处理这些信息了。一共 \(\log n\) 层，每层一次排名（离散化）操作，用 sort 与 lower_bound，即可做到 \(O(n \log^2 n)\)，还是没优化到。

B：先前的解法被排序的是字符串，\(O(\log n)\) 是比较，\(O(n \log n)\) 是排序。而现在，\(O(\log n)\) 是层数，\(O(n \log n)\) 是排序。这两个排序，还是大不一样的。

A：两个关键字，每个关键字的值域都仅到 \(n\) ……基数排序！

B：好！

现在我们来说说代码实现吧。

A：有什么要注意的地方吗？

B：记得：

• cnt 是开了前缀和的（自行了解 基数排序），要清零
• 这里的数值是 rk，id 是排过序后的 rk 的对应下标
• 桶的值域：第一轮排序的范围是 0-256，后几轮都是 \(n\)

调了我三天啊……

#include <cstdio>  
#include <algorithm>  
#include <cstring>  
#include <iostream>  
#define debug(x) printf(x);   
const int M = 1000005;  
int sa[M], rk[M << 1], cnt[M], id[M], prerk[M << 1]; char s[M];  
//sa:排名为 i 的后缀的开头  rk:以 i 开头的后缀的排名  
//id:我们以什么顺序考虑这个数组，rk相当于要排序的数组，id 是排好序的 rk 的下标序列   
void get_sa(char *s, int n){  
    int m = std::max(256, n);  
    for(int i = 1; i <= n; i++) ++cnt[rk[i] = s[i]];  
    for(int i = 1; i <= m; i++) cnt[i] += cnt[i - 1];  
    for(int i = n; i; i--) sa[cnt[rk[i]]--] = i;  
    for(int i = 0; (1 << i) <= n; i++){  
        int t = (1 << i);  
        memset(cnt, 0, sizeof(cnt));  
        for(int j = 1; j <= n; j++) id[j] = sa[j];  
        for(int j = 1; j <= n; j++) ++cnt[rk[id[j] + t]];  
        for(int j = 1; j <= m; j++) cnt[j] += cnt[j-1];  
        for(int j = n; j; j--) sa[cnt[rk[id[j] + t]]--] = id[j];  
        memset(cnt, 0, sizeof(cnt));  
        for(int j = 1; j <= n; j++) id[j] = sa[j];  
        for(int j = 1; j <= n; j++) ++cnt[rk[id[j]]];  
        for(int j = 1; j <= m; j++) cnt[j] += cnt[j-1];  
        for(int j = n; j; j--) sa[cnt[rk[id[j]]]--] = id[j];  
        memcpy(prerk, rk, sizeof(rk));  
        for(int p = 0, j = 1; j <= n; j++){  
            if(prerk[sa[j]] == prerk[sa[j-1]] && prerk[sa[j]+t] == prerk[sa[j-1]+t])  
                rk[sa[j]] = p;  
            else rk[sa[j]] = ++p;  
        }  
    }  
}   
int main(){  
    scanf(" %s", s+1); int n = strlen(s+1);  
    get_sa(s, n);  
    for(int i = 1; i <= n; i++) printf("%d ", sa[i]);  
    return 0;  
}  

有了它，你就能愉快地 AC P3809 了！

另一道练手题： P4051

结束了吗？

B：想想，我们开始说，为了让 SA 的功能接近后缀树，我们还需要什么？

A：LCP。

B：从树上思考，挑选两个后缀是 \(O(n^2)\) 的。为了方便地维护 LCP，可以省略一些东西吗？

A：已经假设了叶子有序，考虑不断往上跳 LCA 时的过程。记以 \(i\) 开头的后缀与与 \(j\) 开头的后缀的 LCP 为 \(lcp(i,j)\)。 如果维护相邻两片叶子的 LCP 的话，从第 \(i\) 片叶子到第 \(j\) 片叶子，可以看成从第 \(i\) 片叶子所在子树不断往上跳到与第 \(j\) 片叶子所在集合汇合。即 \(lcp(sa_i,sa_j) = \min_{i \leq k < j} lcp(sa_i, sa_{i+1})\)

（只能大致表达成这样了QwQ，记得照着前面那棵后缀树意会）

所以我们只需维护 \(lcp(sa_i,sa_{i+1})\) 即可。

B：把 \(lcp(sa_i,sa_{i+1})\) 记作 \(height_i\)。

有引理：\(height_{rk_i} \geq height_{rk_{i-1}}-1\)

浅证：

\(sa_{rk_{i-1}}=i-1:kAB\)

\(sa_{rk_i}=i:AC\)

\(sa_{rk_{i-1}-1}:kAD\)

\(sa_{rk_{i-1}+1}:AD\)

\(sa_{rk_i-1}:AE\)

后两者的 LCP 的长度至少为 \(|A|\)。而 \(kA\) 正是 \(sa_{rk_{i-1}}\) 与 \(sa_{rk_{i-1}-1}\) 的 LCP，长度为 \(height_{i-1}\)，即证。

于是，我们就可以根据这个引理暴力了！反正 \(r\) 至多增加 \(2n\) 次。

for(int i = 1, k = 0; i <= n; i++){  
    if(k) --k;  
    while(s[i+k] == s[sa[rk[i]-1] + k]) ++k;  
    h[rk[i]] = i;  
}   

LCP 没有例题，但是让 SA 发挥后缀树差不多的功能很多需要依赖 LCP。

例题

光学知识点不做题刷AC记录怎么行呢！

题目：UVA12206 & SP10079 & P2852

给定一个长度为 \(n\) 的字符串，以及一个常数 \(k\)，求出现次数至少为 \(k\) 次的最长子串，以及所有满足这个性质的子串中左端点的最右可能。

出现至少 \(k\) 次，意味着至少是 \(k-1\) 个后缀的公共前缀。也就是有连续 \(k-1\) 个 \(height\) 大于 \(0\)。（想想 \(lcp(sa_i,sa_j) = \min_{i \leq k < j} lcp(sa_i, sa_{i+1})\)）

但是我们还要求最长。出现至少 \(k\) 次的最长子串就是所有连续 \(k-1\) 个 \(height\) 的最小值中的最大值（所有 \(\min\) 中的 \(\max\)，用单调队列维护 \(\min\)）。这个可以用单调队列。同时，还要维护连续 \(k\) 个 \(sa\)，来求左端点的最右可能（\(\max\)）。这个用单调队列也可以轻松维护。复杂度 \(O(n \log n)\)，瓶颈在求 \(sa\) 与 \(height\)，后面的处理是 \(O(n)\) 的。

#include <cstdio>  
#include <algorithm>  
#include <cstring>  
#include <iostream>  
#include <set>  
#define clr(x) memset(x, 0, sizeof(x))  
#define debug(x) printf(x);   
const int M = 1000005;  
int sa[M], rk[M << 1], cnt[M], id[M], prerk[M << 1], h[M]; char s[M];  
void get_sa(char *s, int n){  
    int m = std::max(256, n);  
    for(int i = 1; i <= n; i++) ++cnt[rk[i] = s[i]];  
    for(int i = 1; i <= m; i++) cnt[i] += cnt[i - 1];  
    for(int i = n; i; i--) sa[cnt[rk[i]]--] = i;  
    for(int i = 0; (1 << i) <= n; i++){  
        int t = (1 << i);  
        memset(cnt, 0, sizeof(cnt));  
        for(int j = 1; j <= n; j++) id[j] = sa[j];  
        for(int j = 1; j <= n; j++) ++cnt[rk[id[j] + t]];  
        for(int j = 1; j <= m; j++) cnt[j] += cnt[j-1];  
        for(int j = n; j; j--) sa[cnt[rk[id[j] + t]]--] = id[j];  
        memset(cnt, 0, sizeof(cnt));  
        for(int j = 1; j <= n; j++) id[j] = sa[j];  
        for(int j = 1; j <= n; j++) ++cnt[rk[id[j]]];  
        for(int j = 1; j <= m; j++) cnt[j] += cnt[j-1];  
        for(int j = n; j; j--) sa[cnt[rk[id[j]]]--] = id[j];  
        memcpy(prerk, rk, sizeof(rk));  
        for(int p = 0, j = 1; j <= n; j++){  
            if(prerk[sa[j]] == prerk[sa[j-1]] && prerk[sa[j]+t] == prerk[sa[j-1]+t])  
                rk[sa[j]] = p;  
            else rk[sa[j]] = ++p;  
        }  
    }  
    for(int i = 1, k = 0; i <= n; i++){  
        if(k) --k;  
        while(s[i+k] == s[sa[rk[i]-1] + k]) ++k;  
        h[rk[i]] = k;  
    }  
}   
int n; int hs[M], sas[M], l1, r1, l2, r2; //hs需要最小值，sas需要最大值   
int main(){  
    int k = 0;  
    while(scanf("%d", &k)){  
        if(k == 0) return 0;  
        scanf(" %s", s+1); n = strlen(s+1);  
        if(k == 1) {printf("%d 0\n", n); continue;}  
        get_sa(s, n); int l = 1, r = n, ans = 0, pl = 0;  
        l1 = 1; r1 = 0; l2 = 1; r2 = 0;  
        for(int i = 1; i <= n; i++){  
            while(l1 <= r1 && h[hs[r1]] >= h[i]) r1--;  
            hs[++r1] = i;  
            while(hs[r1] - hs[l1] + 1 > k - 1) l1++; //hs 中留 k-1 项   
            while(l2 <= r2 && sa[sas[r2]] <= sa[i]) r2--;  
            sas[++r2] = i;  
            while(sas[r2] - sas[l2] + 1 > k) l2++; //sas 中留 k 项   
            int t = h[hs[l1]], maxpl = sa[sas[l2]];  
            if(t > ans) ans = t, pl = maxpl;  
            else if(t == ans) pl = std::max(pl, maxpl);  
        }  
        if(ans == 0) printf("none\n");  
        else printf("%d %d\n", ans, pl-1);  
        clr(sa); clr(rk); clr(cnt); clr(id); clr(prerk); clr(h); clr(s);  
    }   
    return 0;  
}  

参考资料

炫酷后缀树魔术 - EA

后缀数组 - OI-wiki

谭老师的 ppt

---

分类：笔记