数学寒假作业 - 二次函数与反比例函数

前言

这是数学作业，东西主要是老魏之前讲过的，加点自己现在新的感受吧。

upd 22/4/12：原博客总是渲染失败，明天就要交作业了……只好弄了个新博客……然后发现自己完全不会用……

---

---

 

关于函数与图像

函数：一个确定的映射关系，记作 $F(x)$，其中的变量有且仅有 $x$。$x$ 的取值的集合记为定义域，$F(x)$ 的取值的集合记为值域。

函数的图像：$(x,F(x))$ 的集合，也能写作 $y=F(x)$。

方程：含有未知数的等式。

元：未知数的数量。

次：未知数最高次数。

广义的函数是一个映射关系，其定义域与值域都不必是实数。初等函数（现在研究的函数均属于此）的定义域和值域限于数域（这里是 $\mathbf{R}$）。

在定义域内中任取一数 $x$，将 $(x,F(x))$ 看做平面直角坐标系上的点，由实数的无限性知这样的点有无穷多个。这样无穷多个点的集合被称为这个函数的图像。

若有 $F(x),G(x)$ 两个函数交于点 $(x,y)$，必有 $y=F(x)=G(x)$，所以两个函数图像的交点坐标对应联立两个方程的解，即

$$
\left\{
\begin{array}{}
y=F(x) \\
y=G(x)
\end{array}
\right.
$$

更一般地，将仅有 $x,y$ 为元的方程的解集 $(x,y)$ 看成平面直角坐标系上的点集，这个点集可以被称作原方程的图像。

此时，两个图像的交点即为联立两方程得到的解。两个方程不必是 $y=F(x)$ 形式。

$F(x)=0$ 的解可看成 $y=F(x)$ 与 $y=0$ 的交点的横坐标，即函数 $y=F(x)$ 与 $x$ 轴的交点横坐标。

---

---

 

 

 二次函数与抛物线

一元二次函数可通写成 $F(x) = a \cdot x^2+b \cdot x+c$ 的形式，$y=F(x)$ 为一元二次函数的图像，即抛物线，图像与 $x$ 轴的交点即方程 $F(x)=0$ 的解，函数在 $x$ 轴上方时自变量的取值范围对应 $F(x)>0$ 的解。

一元二次方程可通过配方求为

$$ y = \dfrac{-b\pm \sqrt{b^2-4ac}}{2a}$$

$\Delta = b^2-4ac$ 作为判别式出现，对应二次方程的解数，也对应二次函数与 $x$ 轴的交点数。

---

 

抛物线

定义：到定点与定直线距离相等的点的集合称为抛物线。

设定点（焦点） $F\left(\dfrac{p}{2}, 0 \right)$, 定直线（准线） $y = -\dfrac{p}{2}$

于是 ：

$$
\begin{array}{rll}
\sqrt{\left(x-\dfrac{p}{2}\right)^2+y^2} &=& x + \dfrac{p}{2}\\
x^2-px+\dfrac{p^2}{4}+y^2 &=& x^2+px+\dfrac{p^2}{4}\\
y^2 &=& 2px\\
x &=& \dfrac{y^2}{2p}
\end{array}
$$

同理，$y=\dfrac{x^2}{2p}$ 也为抛物线。

由函数的 “上加下减左加右减” 知 $y=ax^2+bx+c$ 也为抛物线。

---

 

（物理意义上的）抛物线是上述形式的证明

先证匀变速运动公式：$S=v_0t+\dfrac{1}{2}at^2$

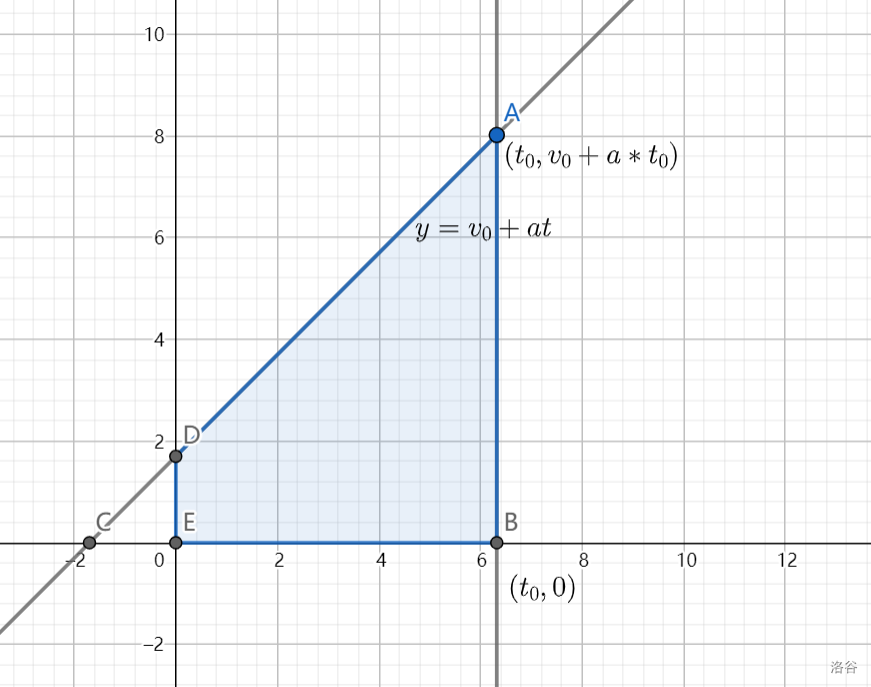
画出速度随时间变化的图像，无限细分时间，路程 = $\sum$ 每一小段时间 * 平均速度（可用其中左端点对应速度代替），即阴影面积。

单位上阴影是二维的，即时间与速度两维，符合对路程的定义。

$$S=S_{\text{shaded}}=\dfrac{v_0 + (v_0+at)}{2} * t_0$$

整理即得匀变速运动公式。

路程是速度的积分，速度是路程的导数。（应该没理解错吧）

以右方与下方为正方向建立平面直角坐标系，从 $(0,0)$ 处抛出一个质点，设其初速度在 $x$ 轴上的投影为 $v_x$，在 $y$ 轴上的投影为 $v_y$。

$$
\left\{
\begin{array}{ll}
x=v_x \cdot t\\
y=v_y\cdot t+\dfrac{1}{2}g\cdot t^2
\end{array}
\right.
$$

代入，即得

$$y = \dfrac{g}{2v_x^2}x^2+\dfrac{v_y}{v_x} \cdot x$$

即

$$y = a x^2 + bx, with \ a > 0$$

其中

$$
\left\{
\begin{array}{ll}
v_x = \sqrt{\dfrac{g}{2a}}\\
v_y = b \cdot v_x
\end{array}
\right.
$$

二次函数是特殊的抛物线。抛物线并不是函数，这可以从 $y^2=2px$ 中直接看出。在二次函数中，一个 $x$ 通过映射对应到特定的 $y$，而在抛物线中一个 $x$ 可能对应2个 $y$，有的可能无法对应上一个 $y$。

---

---

 

 反比例函数与双曲线

反比例函数可通写作 $y=\dfrac{k}{x}$ 的形式，以 $x,y$ 轴为渐近线。

---

 双曲线

到定点距离之差为定值的点的集合为双曲线。

设两定点 $F1(-c, 0), F2(c, 0)$，定差为 $2a$，有：

$$|\sqrt{(x+c)^2+y^2}-\sqrt{(x-c)^2+y^2}|=2a$$

展开整理得：

$$\dfrac{x^2}{a^2}-\dfrac{y^2}{c^2-a^2} = 1$$

即为双曲线标准形式。双曲线的渐近线为 $y = \pm \dfrac{b}{a}\cdot x$

---

---

 

如有错误，敬请提出。