聚类分析与判别分析的区别与联系

背景

松哥常言统计分三级：“初级说一说，中级比一比，高级找关系”；今天所言之题，即为高级找关系之一法。聚类与判别，所谓天下合久必分、分久必合，合则聚类，分则判别。

1.聚类分析

根据研究对象特征对研究对象进行分类的一种多元分析技术, 把性质相近的个体归为一类, 使得同一类中的个体都具有高度的同质性, 不同类之间的个体具有高度的异质性。根据分类对象的不同分为样品聚类（Q聚类）和变量聚类（R）。现实研究中个案聚类常用哦

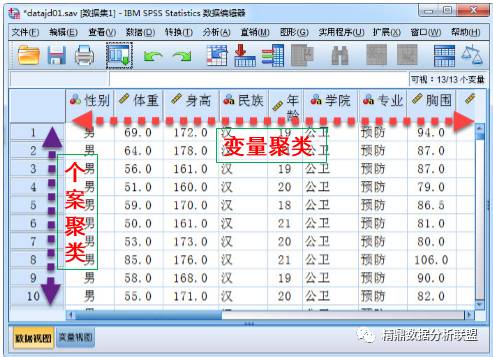
2.判别分析

根据一定量案例的一个分组变量和相应的其他多元变量的已知信息, 确定分组与其他多元变量之间的数量关系, 建立判别函数, 然后便可以利用这一数量关系对其他未知分组类型所属的案例进行判别分组。

判别分析中的因变量或判别准则是定类变量, 而自变量或预测变量基本上是定距变量。依据判别类型的多少与方法不同, 分为多类判别和逐级判别。判别分析的过程是通过建立自变量的线性组合(或其他非线性函数), 使之能最佳地区分因变量的各个类别。

3.区别与联系

1、基本思想不同

( 1) 聚类分析的基本思想

根据相似性( 亲疏关系)，具体找出一些能够度量样品或指标之间相似程度的统计量, 把一些相似程度较大的样品( 或指标) 聚合为一类, 把另外一些相似程度较大的样品( 或指标) 又聚合为另一类; 关系密切的聚合到一个小的分类单位, 关系疏远的聚合到一个大的分类单位, 直到把所有的样品(或指标)聚合完毕。

( 2） 判别分析的基本思想

对已知分类的数据建立由数值指标构成的分类规则即判别函数, 然后把这样的规则应用到未知分类的样本去分类。

2.研究目的不同

虽然都是研究分类的，但在进行聚类分析前，对总体到底有几种类型不知道（研究分几类较为合适需从计算中加以调整）。判别分析则是在总体类型划分已知，对当前新样本判断它们属于哪个总体。

3.聚类分析分两种：Q型聚类（对样本的聚类），R型聚类（对变量的聚类）

聚类分析需要注意的是，一般小样本数据可以用系统聚类法，大样本数据一般用快速聚类法（K均值聚类法），当研究因素既有分类变量又有计量变量，可以用两步聚类。

3.判别分析

有Fisher判别，Bayes判别和逐步判别。一般用Fisher判别即可，要考虑概率及误判损失最小的用Bayes判别，但变量较多时，一般先进行逐步判别筛选出有统计意义的变量，再结合实际情况选择用哪种判别方法。

松哥统计说

聚类为找相似，“物以类聚”；判别是发现不同“人以群分”；

在聚类之前，不知道会聚成几类，而在判别之前，已经知道将会判别为几类。

聚类是没有方程的，判别有方程的；

两者有时联合应用的，如先聚类，根据专业确定几类，然后建立判别模型进行判别。