【数据结构】树状数组
简介
用一下google随手搜索的一张图。
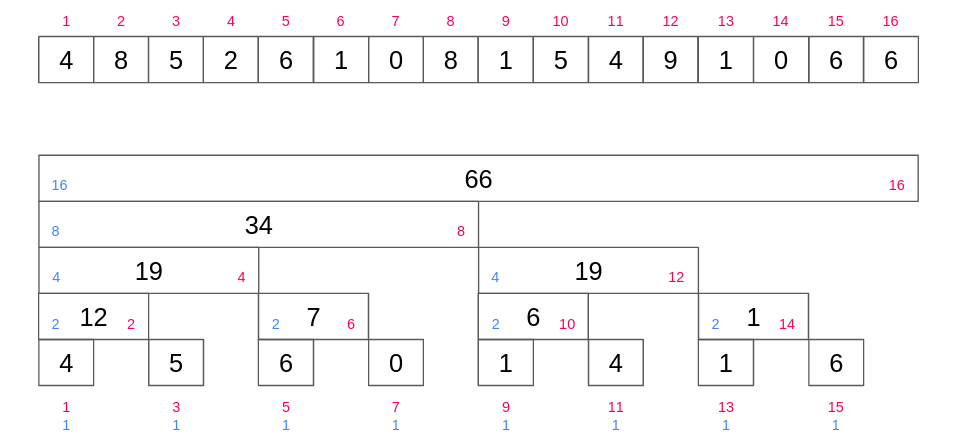
- 首先要理解其中每个节点存储的都是一个连续区间的和。
- 实际上就是一棵线段树把每个节点的右子树直接剪除的结果。
- Add操作的时候,从当前编号的叶子节点开始(不一定是长度为1的层,但一定是叶子),先修改当前节点,然后每次加上当前的层的长度(也就是lowbit)就能到达其正上方的第一层没有缺失的节点。直到到达树根(也就是节点n,最长的节点),不为2的整数幂的n可能会有两个根,这个不影响。
- Sum操作的时候,求得其实是前缀和,也是从叶子节点开始,加上当前节点的和,然后每次减去当前的层长度,就能跳到左上方的节点上。所以注意其实+=lowbit和-=lowbit并不是逆操作,稍微想一想也会知道并不可逆,这两个操作其实都是消除了末尾的1,都是往上层长度更长的节点去跳。
- 如果把Add和Sum操作写反的话,Add的时候往左上角加上了一片,看起来像是一个左右镜像的树状数组,Sum的时候就往正上方跳。感觉整个定义就全部都乱套了,所以一定是错的。
模板
单点加值,区间求和
这个是最基础的树状数组的用法了。初始值是Init之后一个一个Add上去的。
struct BinaryIndexTree {
static const int MAXN = 500000 + 5;
int n;
int sm[MAXN];
void Add(int x, int v) {
for(int i = x; i <= n; i += i & (-i))
sm[i] += v;
}
ll Sum(int x) {
ll res = 0;
for(int i = x; i; i -= i & (-i))
res += sm[i];
return res;
}
void Init(int _n) {
n = _n;
memset(sm, 0, sizeof(sm[0]) * (n + 1));
}
} bit;
已通过:
https://www.luogu.com.cn/problem/P3374
单点改值,区间求和
额外记录一个va数组,然后每次比对这次要“加”的值是多少,套用单点加值。
struct BinaryIndexTree {
static const int MAXN = 500000 + 5;
int n;
int va[MAXN];
int sm[MAXN];
void Add(int x, int v) {
for(int i = x; i <= n; i += i & (-i))
sm[i] += v;
}
ll Sum(int x) {
ll res = 0;
for(int i = x; i; i -= i & (-i))
res += sm[i];
return res;
}
void Init(int _n) {
n = _n;
memset(va, 0, sizeof(va[0]) * (n + 1));
memset(sm, 0, sizeof(sm[0]) * (n + 1));
}
void Modify(int x, int v) {
int d = v - va[x];
Add(x, d);
va[x] = v;
}
} bit;
二维偏序
namespace BinaryIndexTree {
const int MAXN = 200000 + 5;
int n;
int nn;
int a[MAXN];
int aa[MAXN];
int bit[MAXN];
void Add(int x, int v) {
for(int i = x; i <= nn; i += i & (-i))
bit[i] += v;
}
ll Sum(int x) {
ll res = 0;
for(int i = x; i; i -= i & (-i))
res += bit[i];
return res;
}
void Init1() {
n = 0;
nn = 0;
}
void Insert(int v) {
a[++n] = v;
aa[++nn] = v;
}
void Init2() {
sort(aa + 1, aa + 1 + nn);
nn = unique(aa + 1, aa + 1 + nn) - (aa + 1);
memset(bit, 0, sizeof(bit[0]) * (nn + 1));
for(int i = 1; i <= n; ++i) {
a[i] = lower_bound(aa + 1, aa + 1 + nn, a[i]) - aa;
Add(a[i], 1);
}
}
}
区间修改区间求和
设差分数组 \(d_i=a_i-a_{i-1}\) ,显然有 \(a_i=\sum\limits_{j=1}^i d_j\) ,那么 \(Sum(x)=\sum\limits_{i=1}^x a_i=\sum\limits_{i=1}^x \sum\limits_{j=1}^i d_j = \sum\limits_{i=1}^x (x-i+1)*d_i=(x+1)\sum\limits_{i=1}^xd_i - \sum\limits_{i=1}^x i*d_i\) 。
struct BinaryIndexTree {
// const int MAXN = 3e5 + 5;
int n;
ll d1[MAXN], d2[MAXN];
void Add(int x, int v) {
for(int i = x; i <= n; i += i & (-i)) d1[i] += v, d2[i] += 1LL * x * v;
}
ll Sum(int x) {
ll res = 0;
for(int i = x; i; i -= i & (-i)) res += 1LL * (x + 1) * d1[i] - d2[i];
return res;
}
int RangeAdd(int l, int r, int v) {
Add(l, v), Add(r + 1, -v);
}
ll RangeSum(int l, int r) {
return Sum(r) - Sum(l - 1);
}
void Init(int _n) {
n = _n;
memset(d1, 0, sizeof(d1[0]) * (n + 1));
memset(d2, 0, sizeof(d2[0]) * (n + 1));
}
} bit;
Tricks
O(n)建树、权值树状数组求第k小:https://oi-wiki.org/ds/fenwick/
权值树状数组,每个点i记录值为i的节点出现的频率。然后找一个最小的值x,使得小于等于x的所有频率之和恰好>=k。实际上的思路就是“权值线段树上二分”,根节点就是 log2(n) 的下整,每次确定是走左边子树还是走右边子树,先尝试走右边子树,如果爆了(右子树下标越界(不存在此右子树)、加上左子树的全部频次后>=k),就要走左子树。最后找到就是恰好<k的那个值(并且如果遇到0会把0也吃掉,延展到最后一个非0值的左边界),只需要把答案+1,就是刚好>=k的位置。
// 权值树状数组查询第k小
int kth(int k) {
int cnt = 0, ret = 0;
for (int i = log2(n); ~i; --i) { // i 与上文 depth 含义相同
ret += 1 << i; // 尝试扩展
if (ret >= n || cnt + t[ret] >= k) // 如果扩展失败
ret -= 1 << i;
else
cnt += t[ret]; // 扩展成功后 要更新之前求和的值
}
return ret + 1;
}
时间戳优化,不知道是哪个小可爱想出来的不想清空的主意,额外多维护一个tag表示是第x组数据,如果遇到的节点记录的并不是第x组数据的tag,那么就清空它/不计算它。
// C++ Version
// 时间戳优化
int tag[MAXN], t[MAXN], Tag;
void reset() { ++Tag; }
void add(int k, int v) {
while (k <= n) {
if (tag[k] != Tag) t[k] = 0;
t[k] += v, tag[k] = Tag;
k += lowbit(k);
}
}
int getsum(int k) {
int ret = 0;
while (k) {
if (tag[k] == Tag) ret += t[k];
k -= lowbit(k);
}
return ret;
}
感觉没有啥用的一个东西,记录tag不如记录k,reset的时候把add过的k全部强制设为0就好了,或者加上其相反的v(需要额外保存v)。
总之时间戳优化是个画蛇添足的东西。
扩展
权值树状数组/简单名次树:https://www.cnblogs.com/purinliang/p/14265133.html
二维树状数组:单点修改区间查询、区间修改单点查询(转化为差分然后变成第一个问题)、区间修改区间查询(通过看差分数组的使用次数维护额外的差分*使用次数的树状数组):https://www.cnblogs.com/hbhszxyb/p/14157271.html
整体思路跟一维的是一样的。


