P3385 【模板】负环

不能用dijkstra算法 的原因（个人拙见）：

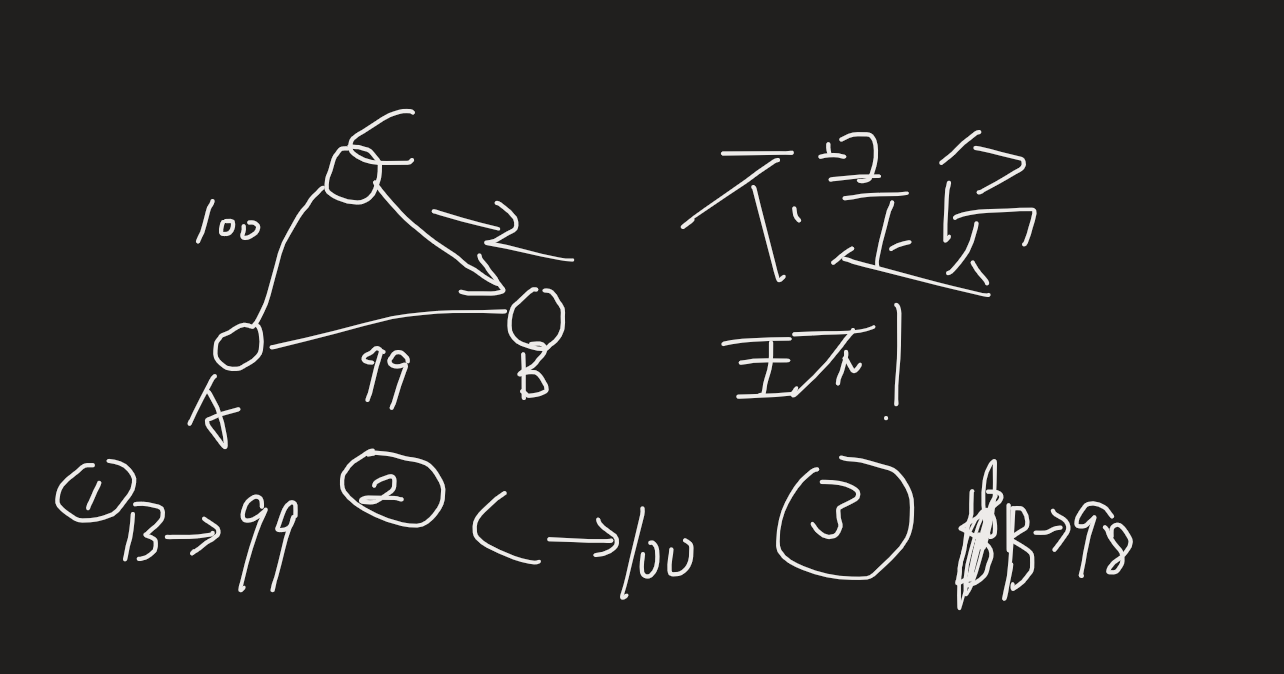
题解

1.思想导论
对于没有负环的图中能到达的任意一个节点，从1出发的最短路径，途中经过的点至少有2个，最多为n个（包括两端）。
设经过的点数为路径的长度
2.思想落实
设cnt[i]为到达i的最短路径的最大长度，每更新一次长度，就更新一次cnt[i]，如果cnt[i]大于n，代表有负环。如果没有负环，更新次数是有限的，是可以退出的。

代码

#include<bits/stdc++.h>
using namespace std;
int n,m;
struct
{
    int head;
    int to;
    int val;
}edge[10004];
int len=0;
int latest[2005]={0};
void add(int u,int v,int w)
{
    edge[++len].to=v;
    edge[len].val=w;
    edge[len].head=latest[u];
    latest[u]=len;
}

int func()
{
    int cnt[2005]={0};
    int dis[2005]={0};
    memset(dis,0x3f3f3f,sizeof dis);
    queue<int> q;
    q.push(1);
    cnt[1]=1;
    dis[1]=0;
    while(!q.empty())
    {
        int now=q.front();
        q.pop();
        if(cnt[now]>n)return 1;
        for(int i=latest[now];i!=0;i=edge[i].head)
        {
            int next=edge[i].to;
            int ren=edge[i].val;
            if(dis[next]>dis[now]+ren)
            {
                dis[next]=dis[now]+ren;
                q.push(next);
                cnt[next]=max(cnt[next],cnt[now]+1);
                if(cnt[next]>n)return 1;
            }
        }
    }
    return 0;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&m);
        for(int i=1;i<=m;i++)
        {
            int x,y,v;
            scanf("%d%d%d",&x,&y,&v);
            add(x,y,v);
            if(v>=0)add(y,x,v);
        }
        if(func())puts("YES");
        else puts("NO");
        memset(latest,0,sizeof latest);
        len=0;
    }
    return 0;
}