MATLAB 非线性最小二乘拟合 lsqnonline 和 lsqcurvefit

MATLAB 中进行非线性最小二乘拟合的函数为：lsqnonline 函数和 lsqcurvefit 函数。帮助文档中的解释为：

lsqnonlin: Solve nonlinear least-squares (nonlinear data-fitting) problem（非线性最小二乘）；

lsqcurvefit: Solve nonlinear curve-fitting (data-fitting) problems in least-squares sense（非线性曲线拟合）。

但是这两个函数本质上是一样的，他们用的默认算法都是：trust-region-reflective，并且都可以修改为：levenberg-marquardt algorithm（详见MATLAB中的帮助文档）。

 

这两个函数的不同在于 lsqcurvefit 的使用形式要更简单一点。下面将结合MATLAB中的帮助文档，简单介绍这两个函数的使用方法。

lsqnonlin 非线性最小二乘

 

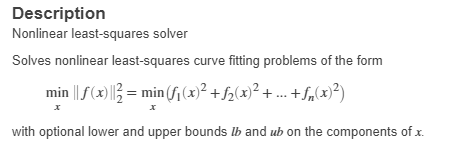
其中，x就是个待辨识的参数，本质就是求满足最适合的参数x，是的拟合误差最小。

% 函数  lsqnonlin 非线性最小二乘
% 格式  
x = lsqnonlin(fun,x0) 
x = lsqnonlin(fun,x0,lb,ub) 
x = lsqnonlin(fun,x0,lb,ub,options) 
% x0为初始解向量；
% lb、ub为解向量的下界和上界lb≤x≤ub，若没有指定界，则lb=[ ]，ub=[ ]；
% options为指定的优化参数；
% lsqnonlin解决非线性最小二乘法问题，包含非线性数据的拟合问题
% 其中初值x0要有。lb，ub，option可为空

 

使用例子，有两种： 

第一种是使用两个文件（其中一个是函数文件，另一个是求解文件）：

首先建立函数文件：

function result = NonlinFun(t)
x = [0.1 0.5 1 1.5 2.5 4.5 6 7];                        % 原函数的输入
y = [29.45 26.65 23.52 20.76 16.16 9.81 6.74 5.25];     % 原函数的输出
a = t(1); b = t(2);                                     % 待拟合的参数
result = y - a*exp(-b*x);                               % 返回拟合结果
end

然后建立求解文件：

% 使用lsqnonlin函数辨识：用两个文件书写，进行非线性最小二乘拟合
clear;
clc;
close all;

a0 = [30 0.2];                              % 待辨识参数的初值 
A = lsqnonlin('NonlinFun',a0)               % 非线性拟合

% 将拟合结果代入函数
xx = 0:0.2:7;
yy = A(1)*exp(-A(2).*xx);
% 这两组数据放在这里只是为了画图使用
x = [0.1 0.5 1 1.5 2.5 4.5 6 7];    　　　　  % 原函数的输入
y = [29.45 26.65 23.52 20.76 16.16 9.81 6.74 5.25];     % 原函数的输出

figure(1);
plot(xx,yy,'r-')
hold on
plot(x,y,'bp')

直接运行求解文件就可以得到结果，结果如下：

 

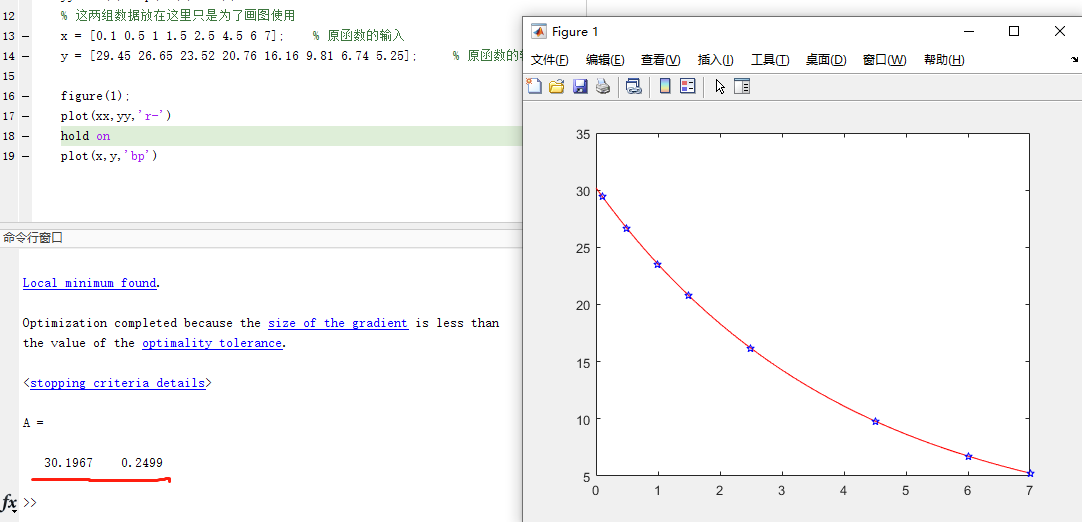
第二种：使用一个文件求解，也就是不使用单独的函数文件：

% 使用lsqnonlin函数辨识：用一个文件书写，进行非线性最小二乘拟合
clear;
clc;
close all;
x = [0.1 0.5 1 1.5 2.5 4.5 6 7];                        % 原函数的输入
y = [29.45 26.65 23.52 20.76 16.16 9.81 6.74 5.25];     % 原函数的输出
fun=@(a)(a(1)*exp(-a(2)*x)-y);                          % 定义函数，其中a待辨识的参数

a0 = [30 0.2];                                          % 待辨识参数的初值 
t= lsqnonlin(fun,a0)                                    % 非线性最小二乘辨识

% 将辨识结果代入函数中
xx = 0:0.2:7;
yy = t(1)*exp(-t(2).*xx);

figure(1)
plot(xx,yy,'r-')
hold on
plot(x,y,'bp')

运行结果如下：

 

 

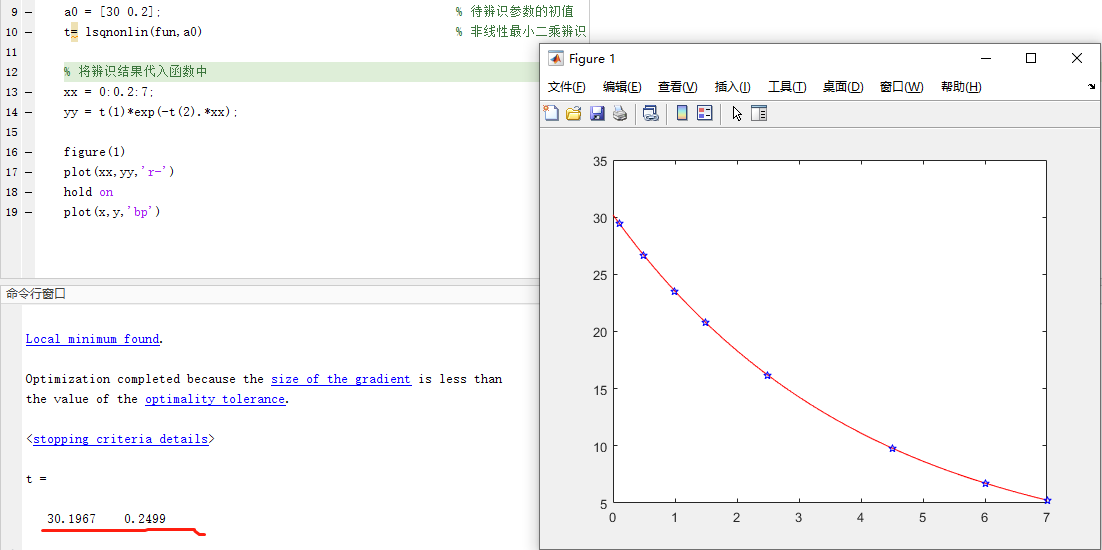
lsqcurvefit 非线性曲线拟合

% 函数  lsqcurvefit 非线性曲线拟合
% 格式  
x = lsqcurvefit(fun,x0,xdata,ydata)
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub)
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)
% 参数说明：
% x0为初始解向量；xdata，ydata为满足关系ydata=F(x, xdata)的数据；
% lb、ub为解向量的下界和上界lb≤x≤ub，若没有指定界，则lb=[ ]，ub=[ ]；
% options为指定的优化参数；
% fun为待拟合函数，计算x处拟合函数值，其定义为function F = myfun(x,xdata)

 

例子：

% lsqcurvefit 非线性曲线拟合：用一个文件书写，进行非线性最小二乘拟合
clear;
clc;
close all;

x = [0.1 0.5 1 1.5 2.5 4.5 6 7];                        % 原函数的输入
y = [29.45 26.65 23.52 20.76 16.16 9.81 6.74 5.25];     % 原函数的输出

a0 = [30 0.2];                                          % 待辨识参数的初值 
f=@(a,x)a(1)*exp(-a(2)*x);                              % 定义函数，a为待拟合的参数,特别注意，需要把自变量x也写到函数变量声明中
t= lsqcurvefit(f,a0,x,y)                                % 非线性曲线拟合

% 将辨识结果代入函数中
xx = 0:0.2:7;
yy = t(1)*exp(-t(2).*xx);

figure(1)
plot(xx,yy,'r-')
hold on
plot(x,y,'bp')

结果：

 

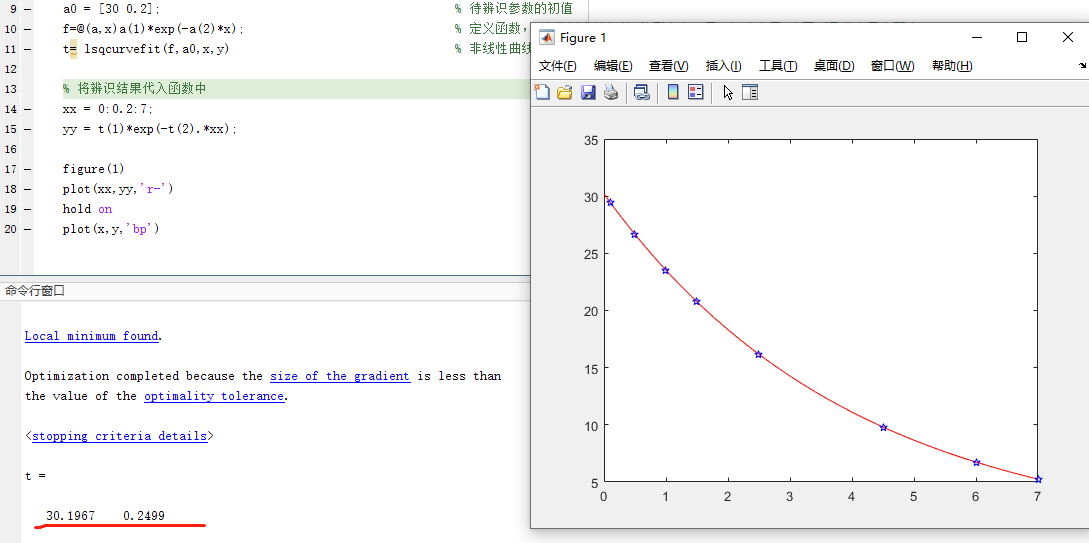
由此可见，上述两个函数的计算结果是一致的。可以发现，这两个函数的做大区别是定义函数的不同：lsqnonline 定义的是误差函数，lsqcurvefit 定义的辨识原函数。

 

局限性：

非线性最小二乘辨识和非线性曲线拟合方法的辨识结果都依赖于初值的选择！当初值给的越接近真实值，辨识出的结果越精确。如果最优解和所给的初值距离比较近，迭代求出最优解的概率就比较大；如果初值设计的不理想，离最优解比较远，而MATLAB对于迭代次数和迭代精度都有个默认的设定，这种情况下很可能没有搜到最优解便给出了结果，也就是这个结果只是局部最优，而不是全局最优。一个比较好的初值选择的思路是：

确定数学模型后,拟合非线性问题时,初值的选取：

1. 如果已知数学模型，有一定物理意义，则建议根据物理意义选取。

2. 当无法确定初值时，且你的数学模型有导数（如果求导模型很复杂甚至没有导数，则可进行简单的差分构造），则可以采用如下的办法进行。

　　　　步骤：

　　　　　    （1）求出拟合函数的一阶导数【如果有必要可求更高阶导数】；

　　　　　　（2）使用已知数据求出近似点的一阶导数 ；

　　　　　　（3）代入一阶导数函数以及原函数求得初值近似值 

 

一个检查初值选取是否合适的思路：得到辨识结果后，画出函数图形，看看已知的数据点是否都在曲线附近，如果相差太大，就得考虑重新给初值再计算一次，直到获得理想的结果。

 

总结：采用最小二乘法进行非线性参数辨识时，容易出现局部最优解，可以使用遗传算法等智能方法进行非线性参数辨识，可以得到全局最优解。