Matrix-tree定理(求生成树的个数)
Matrix-tree定理:对于一个无向图 G ,它的生成树个数等于其基尔霍夫Kirchhoff矩阵任何一个N-1阶主子式的行列式的绝对值。证明:https://blog.csdn.net/can919/article/details/86540819#_58
拉普拉斯矩阵(Laplacian matrix)也可叫做基尔霍夫矩阵: 摘抄自->数学中的各种矩阵大总结
拉普拉斯矩阵是图论中用到的一种重要矩阵,给定一个有n个顶点的图 G=(V,E),其拉普拉斯矩阵被定义为 L = D-A,其中为图的度矩阵,为图的邻接矩阵。例如,给定一个简单的图,如下(例子来自wiki百科):
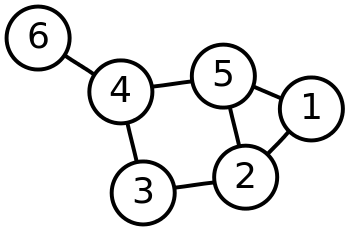
把此“图”转换为邻接矩阵的形式,记为A:

把W的每一列元素加起来得到N个数,然后把它们放在对角线上(其它地方都是零),组成一个N×N的对角矩阵,记为度矩阵D,如下图所示。其实度矩阵(对角线元素)表示的就是原图中每个点的度数,即由该点发出的边之数量。

根据拉普拉斯矩阵的定义L = D-A,可得拉普拉斯矩阵L 为:

显然,拉普拉斯矩阵都是对称的。此外,另外一种更为常用的拉普拉斯矩阵形式是正则化的拉普拉斯矩阵(Symmetric normalized Laplacian),定义为:
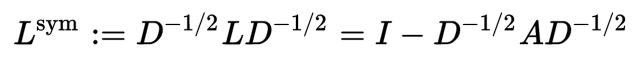
该矩阵中的元素由下面的式子给出:
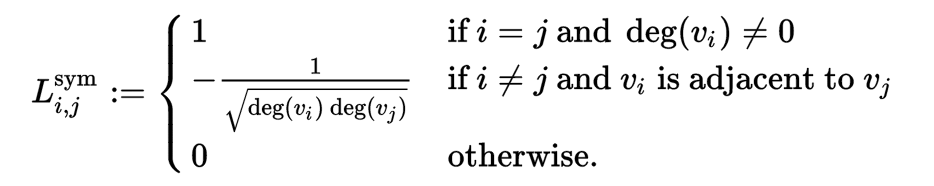
//-----------------------------------------------------------------------------
// 暴力求行列式时间复杂度为 O(N!×N)
//所以要用到高斯消元求矩阵的行列式O(n3) (高斯消元视频讲解很好理解)
//一般方法高斯消元求行列式
// #define rep(i, n) for(int i=0;i!=n;++i)
// #define Rep(i, sta, n) for(int i=sta;i!=n;++i)
int det(int c[][MAXN], int n) {// 高斯消元求上三角矩阵 int ans = 1; rep(i, n) rep(j, n) c[i][j] %= mod; rep(i, n) { Rep(j, i+1, n) { while(c[j][i]) {// 类似辗转相除,可理解为算出c[i][i]和c[j][i]首次为0时把起赋值给c[j][i]() int t = c[i][i]/c[j][i]; Rep(k, i, n) c[i][k] = (c[i][k]-c[j][k]*t)%mod; swap(c[i], c[j]); ans = -ans; } } if(!c[i][i]) return 0; ans = ans*c[i][i]%mod; } return (ans+mod)%mod; }
// hdu 4305
代码参考地->😭
// 这题对结果模10007(素数) 所以能在高斯消元中用逆元↓↓↓
1 /* 2 * @Promlem: 3 * @Time Limit: ms 4 * @Memory Limit: k 5 * @Author: pupil-XJ 6 * @Date: 2019-10-20 14:10:38 7 * @LastEditTime: 2019-10-21 16:25:00 8 */ 9 #include<cstdio> 10 #include<cstring> 11 #include<cmath> 12 #include<iostream> 13 #include<string> 14 #include<algorithm> 15 #include<vector> 16 #include<queue> 17 #include<stack> 18 #include<set> 19 #include<map> 20 #define rep(i, n) for(int i=0;i!=n;++i) 21 #define per(i, n) for(int i=n-1;i>=0;--i) 22 #define Rep(i, sta, n) for(int i=sta;i!=n;++i) 23 #define rep1(i, n) for(int i=1;i<=n;++i) 24 #define per1(i, n) for(int i=n;i>=1;--i) 25 #define Rep1(i, sta, n) for(int i=sta;i<=n;++i) 26 #define L k<<1 27 #define R k<<1|1 28 #define mid (tree[k].l+tree[k].r)>>1 29 using namespace std; 30 const int INF = 0x3f3f3f3f; 31 typedef long long ll; 32 33 inline int read() { 34 char c=getchar();int x=0,f=1; 35 while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} 36 while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} 37 return x*f; 38 } 39 40 const int MAXN = 300+5; 41 const int mod = 10007; 42 43 struct node { 44 int x, y; 45 } p[MAXN]; 46 47 int inv[mod];// inv[i]表示i在%mod下的逆元 48 void init() {// 求逆元(mod质素 才能用递推--素数筛选) 49 inv[1] = 1; 50 Rep(i, 2, mod) inv[i] = (mod-mod/i)*inv[mod%i]%mod; 51 } 52 53 inline int det(int c[][MAXN], int n) {// 高斯消元求上三角矩阵 54 int i, j, k, ans = 1; 55 for(i = 0; i != n; ++i) { 56 for(j = 0; j != n; ++j) { 57 c[i][j] = (c[i][j]%mod+mod)%mod; 58 } 59 } 60 for(i = 0; i != n; ++i) { 61 for(j = i; j != n; ++j) if(c[i][j]) break;// 找出第i行起第i列不为0的行 62 if(i != j) swap(c[i], c[j]); 63 ans = ans*c[i][i]%mod; 64 for(j = i+1; j != n; ++j) {// 第j行第i列变为0 65 int d = c[j][i]*inv[c[i][i]]%mod;// c[j][i]-d*c[i][i] = 0 66 for(k = i; k != n; ++k) {// (c[j][i]->0同时其它c[j][k]减去d*c[i][k], k=i+1 也行,因为k=i没必要) 67 c[j][k] = (c[j][k]-d*c[i][k]%mod+mod)%mod; 68 } 69 } 70 } 71 return ans; 72 } 73 74 inline double get_dis(int i, int j) { 75 return sqrt((double)((p[i].x-p[j].x)*(p[i].x-p[j].x)+(p[i].y-p[j].y)*(p[i].y-p[j].y))); 76 } 77 78 inline bool same(int i, int j, int k) { 79 return (p[j].x-p[i].x)*(p[k].y-p[i].y) == (p[j].y-p[i].y)*(p[k].x-p[i].x) 80 && (p[k].x>p[i].x&&p[k].x<p[j].x || p[k].x>p[j].x&&p[k].x<p[i].x); 81 } 82 83 int main() { 84 ios::sync_with_stdio(false); cin.tie(0); cout.tie(0); 85 int T; 86 T = read(); 87 int n, r, mat[MAXN][MAXN]; 88 init(); 89 while(T--) { 90 n = read(); r = read(); 91 rep(i, n) rep(j, n) mat[i][j] = 0; 92 rep(i, n) p[i].x = read(), p[i].y = read(); 93 rep(i, n) { 94 Rep(j, i+1, n) { 95 if(get_dis(i, j) <= r) { 96 bool ok = true; 97 rep(k, n) if(k != i && k != j && same(i, j, k)) { 98 ok = false; break; 99 } 100 if(ok) {// 构造Kirchhoff矩阵 101 mat[i][j] = mat[j][i] = -1; 102 ++mat[i][i]; ++mat[j][j]; 103 } 104 } 105 } 106 } 107 int ans = det(mat, n-1);// Matrix-tree定理 108 if(ans == 0) cout << "-1\n"; 109 else cout << ans << "\n"; 110 } 111 return 0; 112 }


