最小生成树——Kruskal算法

连通无回路的无向图称之为树，如果无向图G的生成子图T是树，则称T是G的生成树，生成树不止一种，其中各边权值和最小的树被称为最小生成树。

• 边数等于点数减一
• 没有环
• 图连通并且边都为桥（就是说去掉任意一条边，图就不再连通）
• 两点间路径唯一
• 边权和最小
  

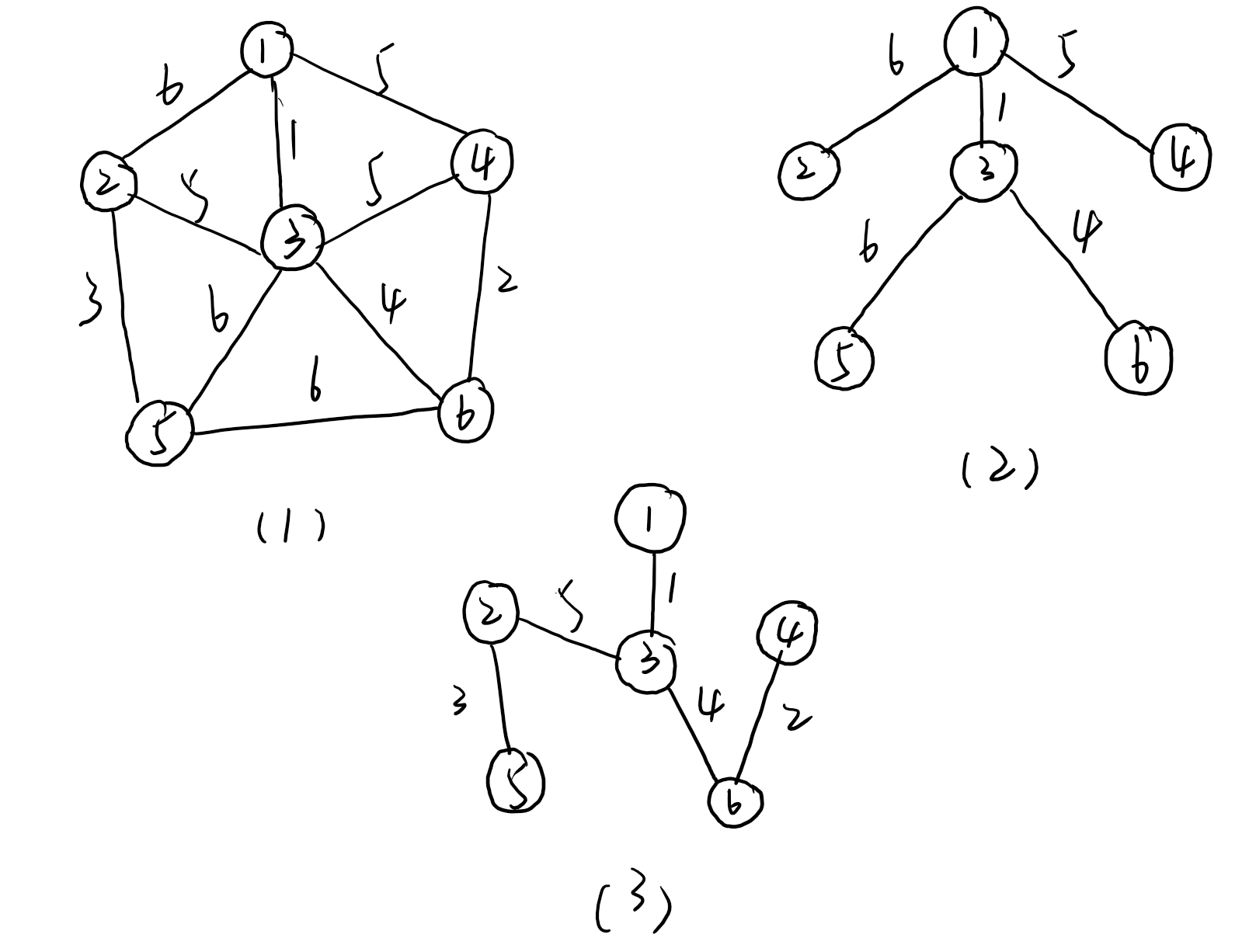
其中（1）为原无向图，（2）为其中一种生成树，（3）为其中一种最小生成树。

---

思维

kruskal算法也是一种贪心的算法，去除n阶无向图中所有的边，然后每次挑选所有边中权值最小的那一条边相连，如果连边会导致图形成环，就抛弃这条边，去寻找下一条边，直到图上存在n-1条边位置，即可得到最小生成树。
其选边过程为：

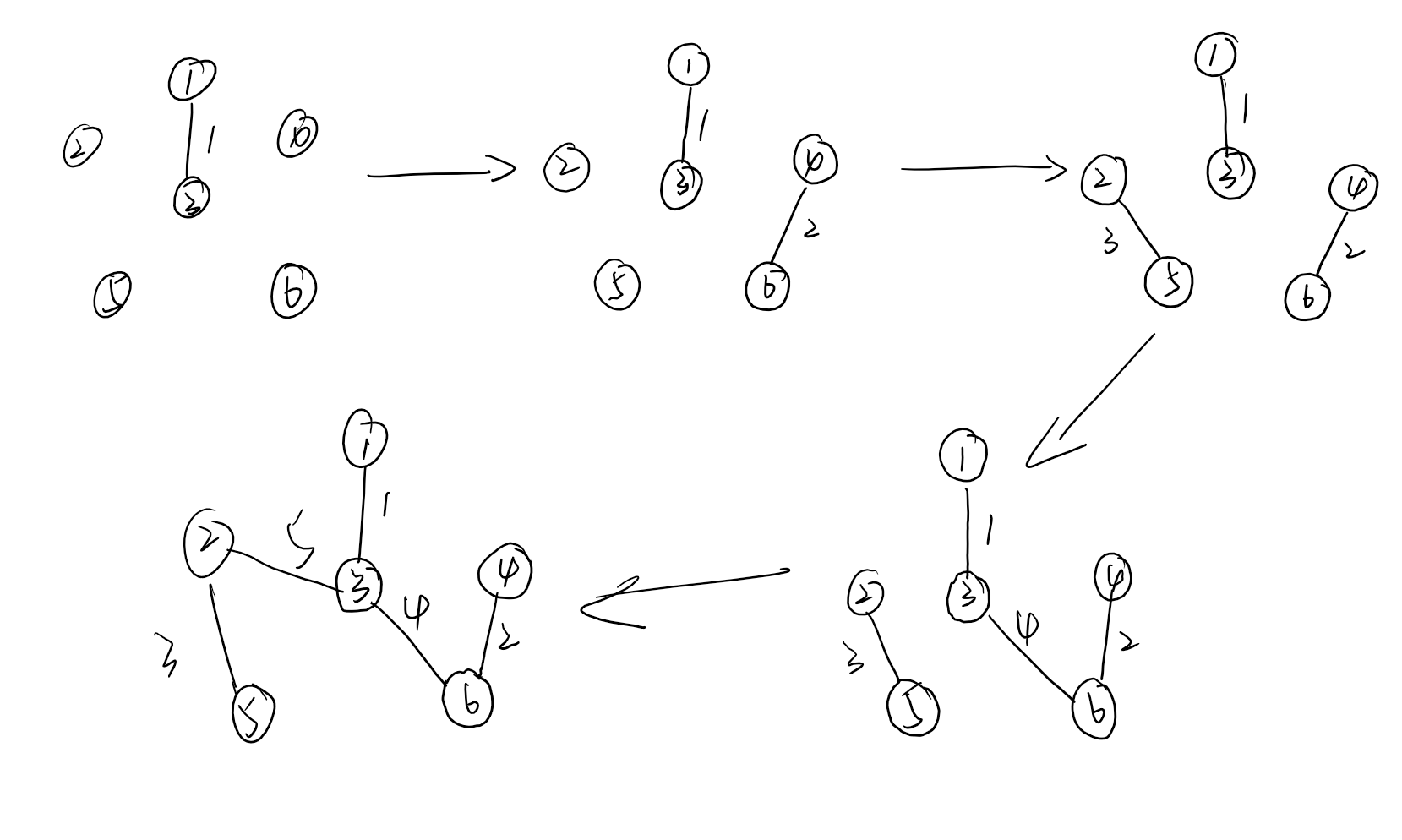
所以算法实现先对所有边按照权值进行排序，在以贪心思想接连构成边。采取避环的思想，直到得到一颗最小生成树。
其中实现的难点在于如何判断构成了环，首先利用搜素的思想遍历当然是可行的，但是时间复杂度较高。所以这时候就能用上之前提到过的并查集，当处于同一个集合的时候便可以判断二者之间有通路，若在链接便会构成环。
给出之前并查集的传送门：(https://www.cnblogs.com/pullself/p/10053829.html)

---

代码实现

时间复杂度为O(mlogm)

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
const int MAX = 200005;

int pre[50050], ran[50050], ans = 0;

struct edge {
	int x, y;
	int w;
}e[MAX];

bool cmp(edge a, edge b) {
	if (a.w != b.w) return a.w < b.w;
	else return a.x < b.x;
}

void make_pre(int i)
{
	pre[i] = i;
	ran[i] = 0;
}

int find_pre(int i)
{
	if (pre[i] == i)
		return pre[i];
	return  pre[i] = find_pre(pre[i]);
}

int unite(int x, int y, int w) {
	int rootx, rooty;
	rootx = find_pre(x);
	rooty = find_pre(y);
	if (rootx == rooty) return 0;
	if (ran[rootx] > ran[rooty]) {
		pre[rooty] = rootx;
	}
	else {
		if (ran[rootx] == ran[rooty]) ran[rooty]++;
		pre[rootx] = rooty;
	}
	ans += w;
	return 1;
}

int main() {
	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= n; i++) make_pre(i);
	for (int i = 1; i <= m; i++) {
		int x, y, w;
		cin >> x >> y >> w;
		e[i].x = x;
		e[i].y = y;
		e[i].w = w;
	}
	sort(e + 1, e + m + 1, cmp);
	ans = 0;
	int count = 0;
	for (int i = 1; i <= m; i++) {
		int flag = unite(e[i].x, e[i].y, e[i].w);
		if (flag) count++;
		if (count == n - 1) break;
	}
	cout << ans << endl;
	return 0;
}