ResNet v2笔记
1、简介
深度参残差网络由许多的残差块构成,在v1版本里,残差块可由公式表述如下:
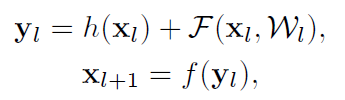
h(x)=x,这是一个恒等映射;F是残差函数;f是ReLU激活函数。这篇论文的主要工作是构建了信息传播的直接通道——不仅是在残差块内部,而且在整个网络中都能够高效地传递。作者通过推导证明了:如果h(x)和f(x)都是恒等映射的话,那么信号能够直接从一个残差块传递到另一个残差块,无论是在前向传播还是反向传播的过程中。

如上图所示,左图(a)是在v1中使用的残差块结构示意图,右图是在这篇文章中使用的结构。与v1版本相比,v2将激活函数都放在了求残差这条支路上,这样一来,在反向传播和前向传播中,信息的传播速度都会很快,这使得网络唔够得到更好的效果,并且这种结构也防止了梯度消失的问题。
2、残差网络分析:
V1版本的残差块使用公式描述如下:
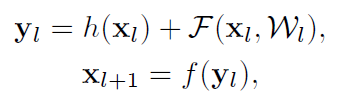
在这里,如果我们假设f也是恒等映射,那么就有:
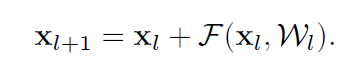
递归地可以求得:

这个公式有着两个非常好的特性:
1、任意的都可以表示为与残差项的和;2、任意的都是前面预测的各残差项之和;这与v1版本有着很大的区别(v1版本中如果忽略BN和ReLU)则可以看成是逐项相乘;
对损失函数求导可得:
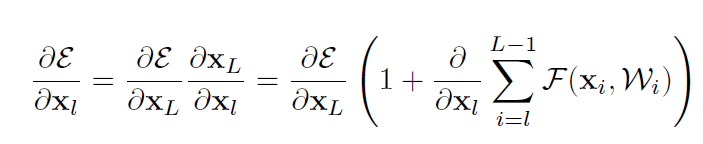
可以看到,梯度可以被分解为两项:一项是,另一项与这一项相加构成了梯度的全部信息。第一项就保证了梯度能够被直接从L层传递到第l层;此外,这个公式还表明不会为零,因为括号里的后一项不会始终为-1,这就避免了梯度消失的问题。
3、当h(x)不为恒等变换且f(x)也不是恒等变换时,模型的效果如何?
我们先从公式上来分析:假设h(x)是在恒等变换的基础上乘以因子λ,那么XL为:
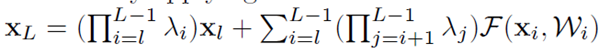
λ的引入对上式会产生很大的影响:1、λ>1时,上式很有可能会出现爆炸的情况,0<λ<1时,上式很有可能会趋于零。这对优化造成了困难。
基于这种情况,作者做了几组对照实验,将它们与原始的残差结构进行对比,实验结果如下:
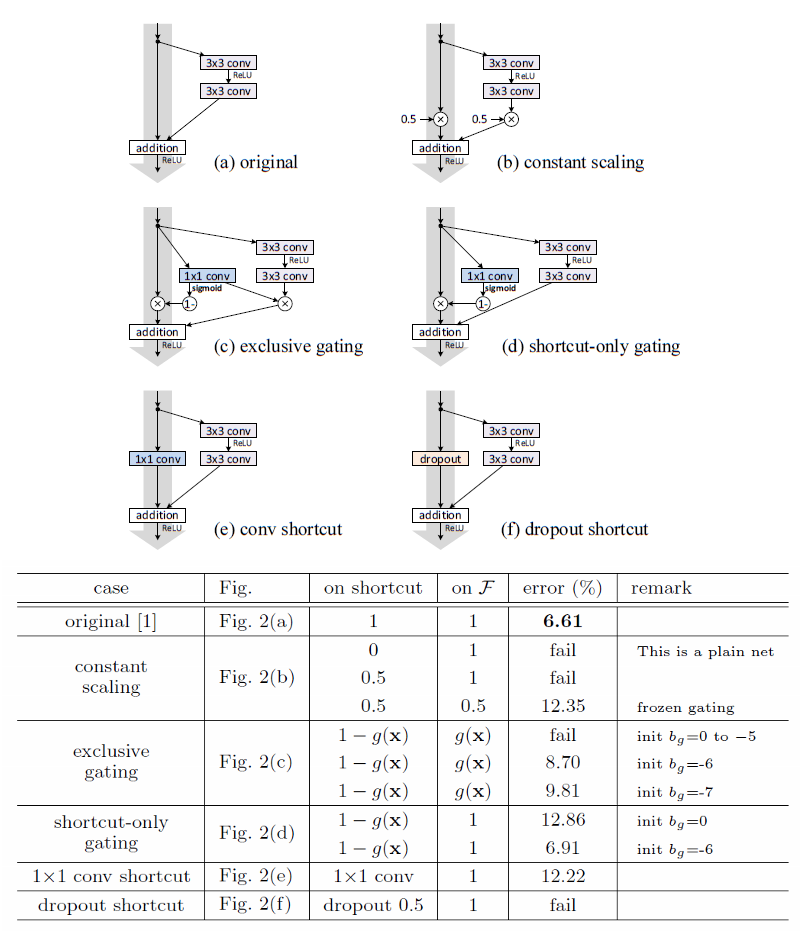
从上面的实验结果可以看出:原始的残差结构的表现是最好的,其他的一些残差结构效果更差,甚至在训练时都不能收敛;值得注意的是,实施了1×1卷积和shortcut-only gating的残差块结构的网络应该是包含了原始网络(使用最初的残差块结构)的解空间的,也即这两个网络的表示能力其实是比原始网络要强的,这更说明模型难以优化是导致这两种模型效果不如原始网络的的原因。
4、激活函数的使用对网络的影响如何呢?
下面是几种残差块网络结构示意图:
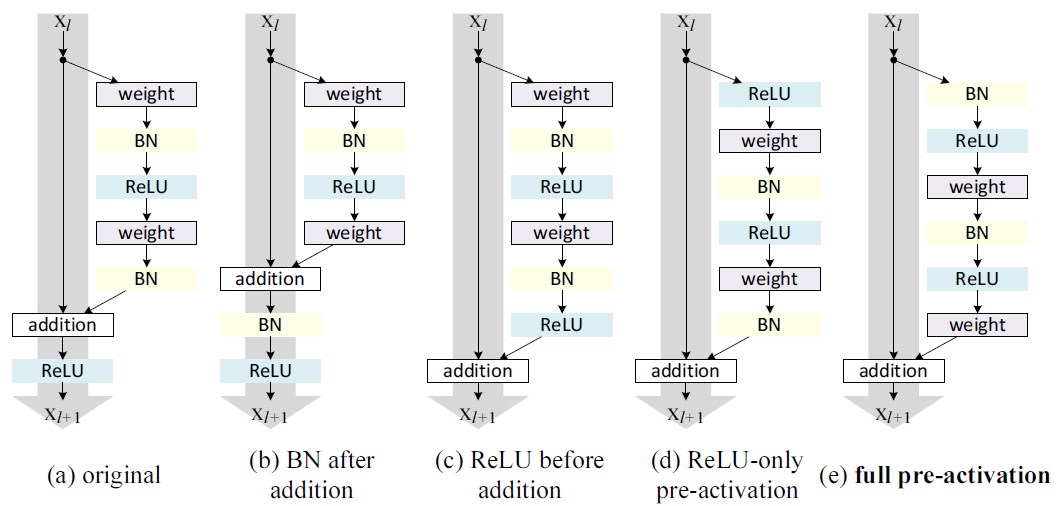
图(a)是原始的网络结构,灰色的大箭头是信息传播最快的方向,可以看到在灰色箭头上还有加和和激活函数。如果想要是恒等变换的话,那么我们酒的重新排列ReLU和BN的顺序,也就是在图中灰色箭头的方向上只有加和而没有激活函数和BN,激活函数和BN就只能放入残差函数中。在上图中,图(c)、(d)、(e)是这三种结构。
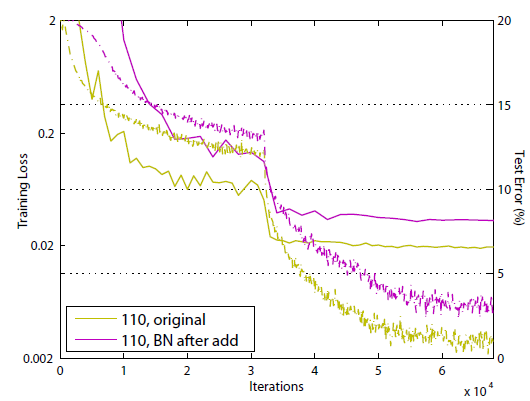
图(b)与我们想要的结构刚好相反:它将BN放在了加和之后,这阻碍了信息的传播,具体表现为模型的收敛速度更慢,如下图所示:
显然,这种方式是不可取的。我们在来看后面几种结构。先来看(c)中的结构:
它将激活函数放在了加和之前,我们知道ReLU的值域为[0,],就是说残差函数的输出始终非负,而直观地讲,我们希望残差函数的输出能够是[,],因此可以预见这个模型的表达能力是受到抑制的,实验结果也证实了这一点(实验结果见下图)。
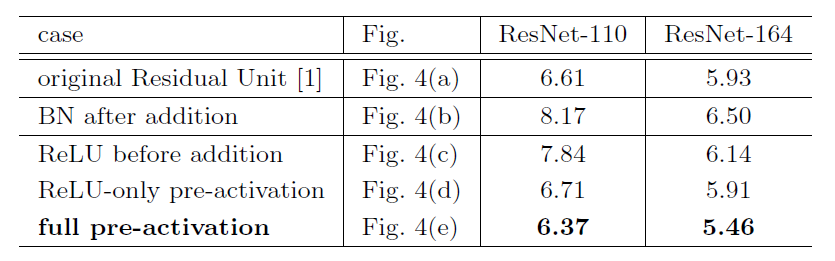
可以看到,(c)结构的效果是不如原始结构的。基于此,我们将激活函数放在最终的输出之前,也就是在获取输入后先对输入进行激活,然后再将激活值归一化,再与权重层相乘,最后输出。注意这里BN的位置与一般的位置有所不同,一般地,BN会在输入与权重相乘之后实施,然后再激活。具体的实施有两种方案:一种是只将激活放在权重层之前,另一种是将BN层也放在权重层之前。两种结构的性能如上表所示。从表中可以发现,只将ReLU放在权重层之前的结构与原始的网络表现类似;而将BN也放在权重层之前的结构的性能则得到了大幅提高。为什么先对输入进行激活的模型有着更好的性能呢?我们分析原因如下:
1、相比于原始的网络结构,先激活的网络中f是恒等变换,这使得模型优化更加容易。
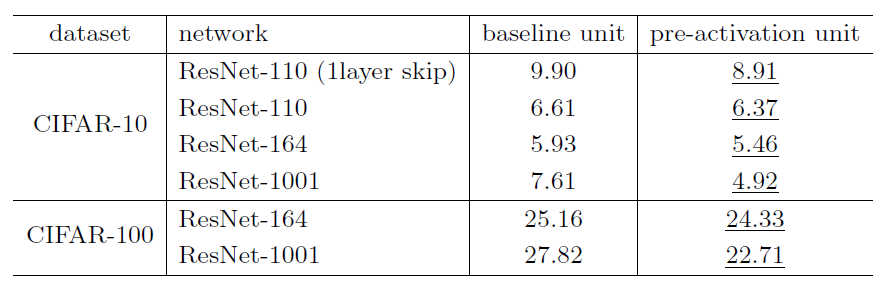
上表是原始网络与先激活网络在不同层数,不同测试条件下的对比结果,使用了先激活输入的网络在所有的测试条件下表现都更好。
2、使用了先激活输入的网络,能够减少网络过拟合。
使用了先激活的网络在的训练误差均比原始网络要高,但是其测试误差却要低于原始网络。作者分析这可能是BN层的作用,在原始网络中,虽然残差函数的输出被归一化了,但是这个归一化的结果与残差块的输入直接相加作为下一个残差块的输入,这个输入在与权重层相乘之前并没有被归一化;而在先激活的网络中,输入与权重层相乘之前都被归一化了,所以有着更好的性能。
这是残差网络的第二篇笔记,后续还有v3,待我仔细研读之后再来更新!!!




