ResNet论文笔记

前段时间仔细的阅读了孙剑老师和何凯明老师在2015年的大作：Deep Residual Learning for Image Recognition。读完就一个感受：这思路太精妙了，关键这篇论文写的还非常好懂，敬佩之情溢于言表啊！！！这篇博客主要记录下残差网络这篇论文的主要内容。

作者首先抛出了一个问题：在ImageNet竞赛中，层数很深的网络能够获得很好的结果，那么仅仅是简单地将网络层数堆叠地更多就能够获得更好的结果吗？其实不然，在这之前就有人在这方面作过实验，并出现下面这样的现象：

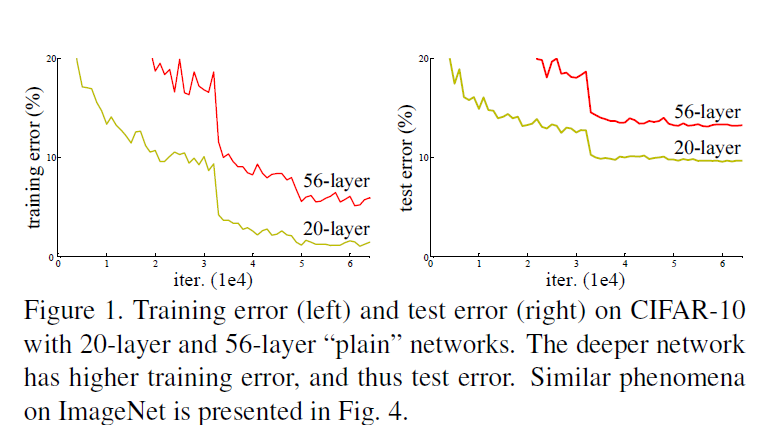
有人用同样的数据训练了两个网络，分别为20层和56层，上图是这个实验的对比结果：

左图是两个网络的训练误差，右图是两个网络的测试误差。我们先看右图，可以发现56层的网络的在测试集上的表现不如20层的网络，按照以往的经验，我们会认为这是由于56层的网络发生了过拟合，但是再看左图，我们会惊奇地发现56层地网络甚至在训练集上地表现都不如20层的网络，这与既有的经验不符。这个现象被称为：degradation problem，也就是退化问题。这个现象说明退化问题不只是由于过拟合造成的，而是由于网络层数的加深使得模型更难优化了。

有什么解决办法呢？那就是重构模型。在浅层网络的基础上叠加更多层，如果叠加的这些层学习到的是恒等映射(identity mapping)，那么这个深层网络的训练误差至少不应该高于浅层网络。但是让网络去学习恒等映射这一点并不容易做到。

因此，作者提出了这样的思想：如果可以学习到恒等映射，那么与其让叠加层去学习这个完整的映射，还不如去学习在浅层网络上的变化是什么，如果确实是恒等映射的话，那么叠加的这一层的参数应该被压缩至零。下面截图是论文原文。

 

残差块的结构：

在上面的结构中，x是输入，经过两层卷积后，将F(x)与x做加和，然后再使用激活函数进行激活。这里采用直接相加的好处是不会增加计算复杂度。看到这里，可能有人会想到F(x)与x做加和时二者的维度不一致怎么办？关于这点，作者再论文中提到有两种解决办法：1、有维度不一致的情况就使用零填充，将不足的部分用0补齐；2、使用1×1卷积将二者的维度变换到一致，很明显第二种方法会引入更多的参数。

恒等映射使用公式表示为：

 

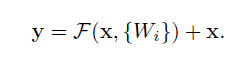
关于残差块有一点需要注意：论文中采用的结构是每两层或者三层卷积构成一个残差块，也可以使用别的层数，这个是没有固定限制的，但是层数不能为1，因为当层数为1的时候，上面的公式就变成了：y=Wx+x，中间的非线性映射就不存在了，即这是一个线性层，这与一般网络的单层没有什么区别，作者也没有发现此时网络会表现地更好。

残差网络的结构：

作者借鉴了VGG网络的思想：所有的卷积核均使用3×3大小，每两层卷积设置为一个残差块。作者一共设置了几种不同深度的网络，在较深的网络中，残差块与较浅的残差网络不同，具体见下图：

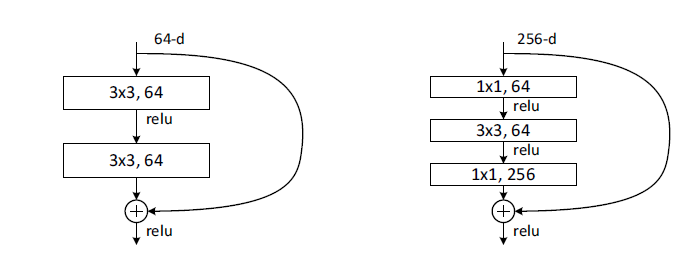
在右边的结构中使用了1×1卷积，这是因为：输入的深度为256，如果直接做卷积运算的话计算量和参数都会非常大，因此先使用了1×1卷积降维，再使用了1×1卷积升维。

到此，残差网络的主要思想就总结完成啦！！！