简介
本次作业我选择的题目是最大连续子数组和,下面我将详细写出我解决此次问题的过程。
题目
最大连续子数组和(最大子段和)
背景
问题:给定n个整数(可能为负数)组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0,依此定义,所求的最优值为: Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如,当(a[1],a[2],a[3],a[4],a[5],a[6])=(-2,11,-4,13,-5,-2)时,最大子段和为20。
-- 引用自《百度百科》
具体要求:
- (1) 请从上述两个题目中根据个人实力任选一题,要求写出可运行的完整代码提交至GitHub或者Coding.net系统中,并将代码地址附到博客内,题目(1)可以参考这篇博文
- (2) 请从语句覆盖、判定覆盖、条件覆盖、判定/条件覆盖、条件组合覆盖五个覆盖标准中(条件组合覆盖难度较大,鼓励尝试,但请谨慎选择),任选一个标准设计测试用例
- (3) 请利用自动测试工具对程序进行测试
- (4) 请将程序运行结果和自动测试分析结果截图附到博客中
问题分析
首先看到题目,我想到了用几个循环嵌套在一起来进行计算和比较,最终算出所有的子数组的和进行比较,但是发现自己还是too young too simple,算法过于暴力以至于时间复杂度一度达到了\(\ O(n^3)\),这样的话需要花费相当多的时间,短短10个数就要计算操作1000次,我不由得推了推我的黑框眼镜......(你够)
因此我想到了动态规划算法,这种算法可以减少时间复杂度,将复杂度降为\(\ O(n)\)。但是这时问题来了,我并不会动态规划的思想,只知道有这个算法而不知道如何使用..........于是我就去了B站,看了一个关于动态规划算法的视频,地址如下:
https://www.bilibili.com/video/av16544031?from=search&seid=2974022978979002224
看过这个视频并且认真学习后,我懂了动态规划算法就是将一味的重复操作减少,将后续需要用到的数据先存储起来,这样就可以避免做多余的重复操作。
下面开始用动态规划的思想分析一下题目的算法。

还有一个问题就是子数组不一定非要从a[0]开始,原因如下:

根据如上分析,我决定在计算时建立两个数组,一个用来保存当前所有子数组的绝对最大值,另一个用于存放指针所指向的数时加上前面的子数组是否会使自身变小来确定当前子数组的最大值。
编程
有了上面的编程思想,那么现在就将思想转换为实际的代码。
int Cal::Max(int a[], int n)
{
int flag = 0;
int temp[100], maxSum[100];//用于存放当前子数组最大值和绝对子数组最大值
temp[0] = maxSum[0] = a[0];//从a[0]开始判断
for (int i = 0;i < n;i++)//判断数组是否全为负数,全为负数则返回0
{
if (a[i] >= 0)
{
flag = 1;
}
}
if (flag == 0)
{
return 0;
}
else
{
for (int i = 1;i < n;i++)
{
temp[i] = max(temp[i - 1] + a[i], a[i]);//判断a[i]的数据与a[0]...a[i]之和数据的大小
maxSum[i] = max(maxSum[i - 1], temp[i]);//判断前一个绝对最大值和当前的最大值的大小
}
return maxSum[n - 1];//返回绝对最大值,即此时最大子数组的和
}
}
coding代码地址:https://coding.net/u/littlepudding/p/SoftwareHomework3/git?public=true
单元测试
单元测试好处不少,谁说对了就让他单元测试~~
如果数据少,则人工输入相对简单,但是比如要输入\(\10^6\)个数,人工输入差不多就是没法实现了....因此编写单元测试代码会节约很多时间,还可以自动判断,大大减少工作时间,提高工作效率。
本次测试使用条件覆盖
条件覆盖:执行足够的测试用例,使得判定中的每个条件获得各种可能的结果。即每个条件至少有一次为真值,有一次为假值。
优点:条件覆盖比判定覆盖,增加了对符合判定情况的测试,增加了测试路径。
缺点:要达到条件覆盖,需要足够多的测试用例,但条件覆盖并不能保证判定覆盖。条件覆盖只能保证每个条件至少有一次为真,而不考虑所有的判定结果。
流程图

测试数据
为了满足判断条件,设置三组测试数据:
第一组:[-2,11,-4,13,-5,-2],最大值为20,这组数据满足判断不全为负数时所有的条件判断
第二组:[ -1,-2,-3,-4,-5,-6 ],最大值为0,这组数据全为负数,满足判断条件中的全为负数
第三组:[-2,2,-3,4,-1,2,1,-5,3],最大值为6,这组数据的满足条件同第一组数据。
编写代码如下:

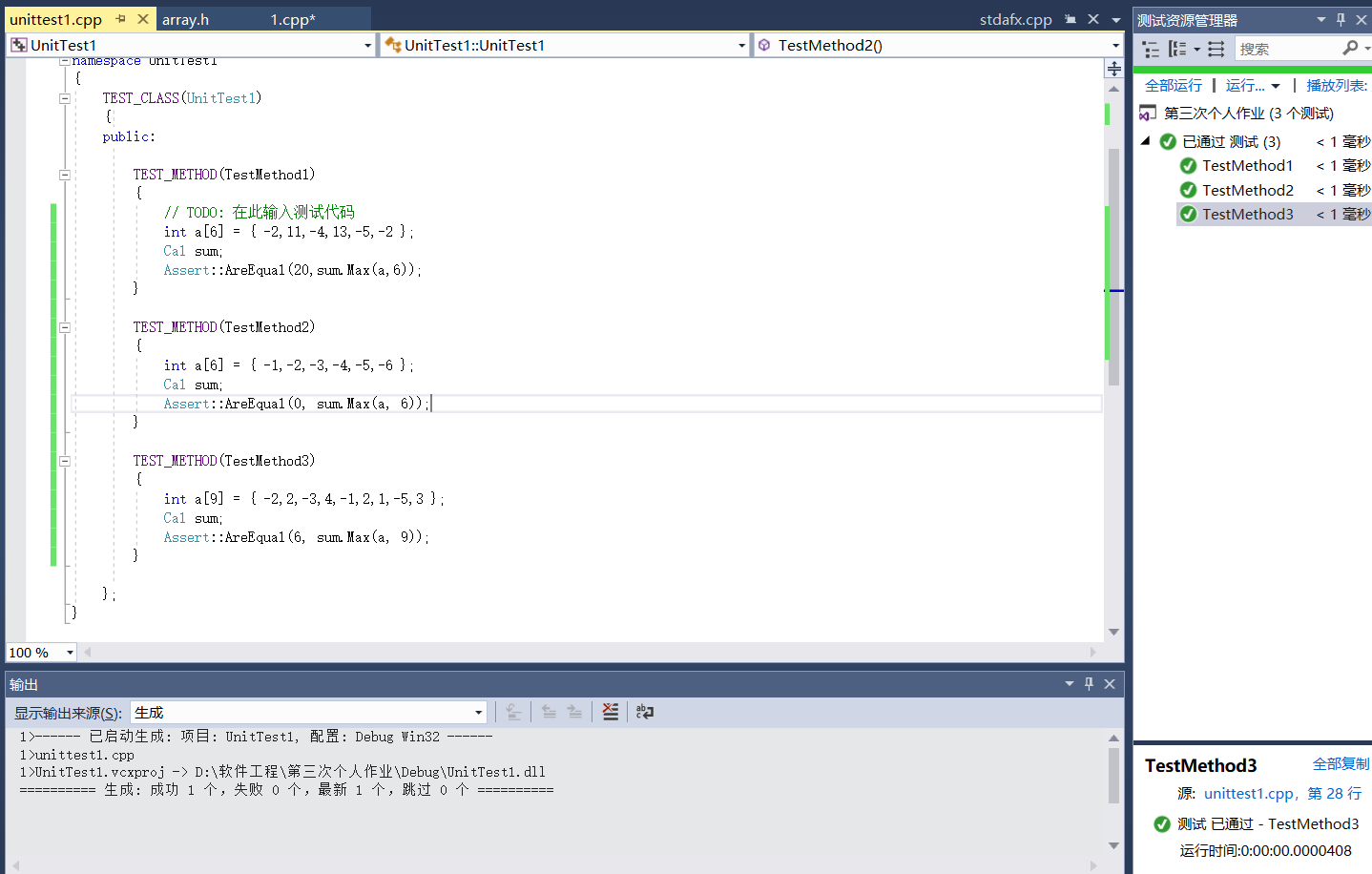
测试结果
如下图,全部通过测试。
PSP2.1表格
| PSP2.1 | Personal Software Process Stages | 预计时间(分钟) | 实际时间 |
|---|---|---|---|
| Planning | 计划 | 15 | 10 |
| · Estimate | · 估计这个任务需要多少时间 | 15 | 10 |
| Development | 开发 | 135 | 175 |
| · Analysis | · 需求分析 (包括学习新技术) | 45 | 60 |
| · Design Spec | · 生成设计文档 | 15 | 20 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 10 | 10 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 10 |
| · Design | · 具体设计 | 20 | 25 |
| · Coding | · 具体编码 | 15 | 25 |
| · Code Review | · 代码复审 | 10 | 10 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 10 | 15 |
| Reporting | 报告 | 90 | 110 |
| · Test Report | · 测试报告 | 60 | 80 |
| · Size Measuremen | · 计算工作量 | 10 | 10 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 20 | 20 |


