卡特兰数与翻折法

膜拜 dy 老师，更建议去看 dy 老师 的！

（有不少图是盗的，大部分内容是抄的。）

考虑一个网格行走的问题，在一个平面直角坐标系中，要从 $(0, 0)$ 走到 $(n, n)$（ $n \geq 1$ ），每次只能向右或向上走一单位长度，并且要求在任意时刻，你所在的坐标 $(x, y)$ 满足 $x \geq y$，也就是不能越过第一象限的角平分线。

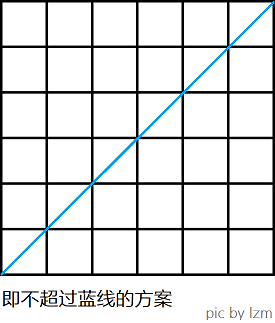
part1

我们设 $cat_n$ 表示卡特兰数第 $n$ 项，也就是从 $(0,0)$ 走到 $(n,n)$ 的方案数。

一个思路是缩小问题规模，转化为子问题，我们考虑枚举一下路径最后一个在 $x=y$ 上的点 $i$。

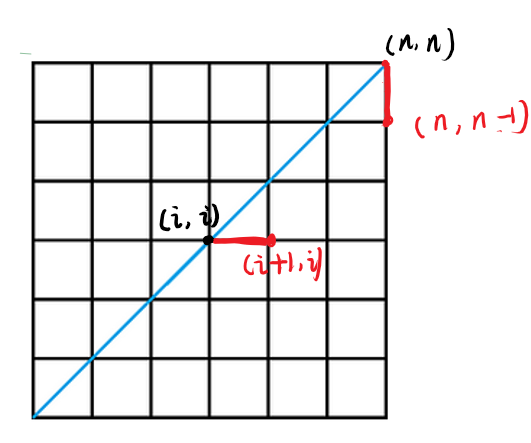
那么不难发现接下来 $(i,i)$ 只能往 $(i + 1, i)$ 走，而最后一步只能是从 $(n, n - 1)$ 走到 $(n, n)$。

现在的问题等价于找 $(i + 1, i)$ 到 $(n, n - 1)$ 的方案数，满足路径中的点任意时刻不会超过 $(i + 1, i)$ 与 $(n, n - 1)$ 之间的那条连线。

你发现这定义其实就是题目要求，将其平移到起点位置，发现是求 $(0, 0)$ 到 $(n - i - 1, n - i - 1)$ 的合法路径条数。

然后变成了一个子问题！

于是 $cat_n = \sum_{i = 0}^{n - 1} cat_i \times cat_{n - i - 1}$。

求解复杂度 $O(n^2)$。

part2

假如没有这个限制，那么等价于在 $2n$ 步中，$n$ 步向右，$n$ 步向上的不同方案数，答案就为 $\dbinom{2n}{n}$。

然后考虑容斥减去不合法的方案数也能得到最终的答案。

如果一种路径方案不合法，那么这条路径上至少有一个点碰到了 $y = x + 1$。

假设第一次碰到 $y = x + 1$ 的点为 $p$，将 $p$ 之后到 $(n, m)$ 的路径关于直线 $y = x + 1$ 对称。

下图中绿线为 $y = x + 1$，红线为源路径越过第一象限角平分后的部分，蓝线为关于 $y = x + 1$ 对称后的结果。

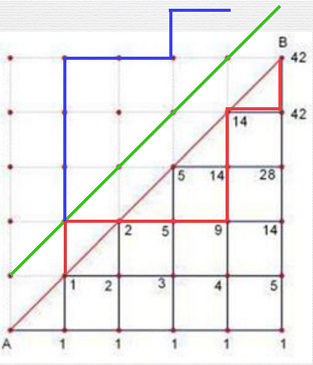
所以任意不合法路径对称后都能唯一对应一条从 $(0, 0)$ 到达 $(n - 1, n + 1)$ 的路径，并且任何一条从 $(0, 0)$ 到 $(n - 1, n + 1)$ 的路径也能唯一对应一条不合法的原路径，二者构成双射，那么不合法路径的数目就为 $\dbinom{2n}{n + 1}$。

所以答案为 $\dbinom{2n}{n} - \dbinom{2n}{n + 1}$。

这种思想就是翻折法，对于不合法的进行单独的考虑，然后通过类似翻折的技巧对应到另一种双射的情况，然后进行另外的求解，之后容斥计算。

有点事情，等没事的时候再回来更新，但是先发出来了。