20220921 模拟赛

T1 彩票

---

\(n \leq 10^5\)。

发现三等奖有三种情况，一等奖和二等奖却都只有一种情况，感觉很烦，考虑暴力做掉三等奖的彩票号码，直接三重循环枚举，这一部分消耗 \(O(\dfrac{100^3}{6})\)。

然后对于一等奖和二等奖的部分，现在要求最多的奖金，考虑将每个手上的彩票统计每种后六位和后四位的分别的个数，然后因为我们只关心后两位不同，然后就只保留后两位。

一等奖和二等奖中肯定都是选择自己能选的个数最多的后两位所代表的数，当然有可能出现先让二等奖最大后让一等奖更大的情况，于是枚举一下先后顺序，然后贪心做两遍即可，每次做的时候扫一下所有合法的后两位数然后取最大的。

时间复杂度 \(O(\dfrac{100^4}{6})\)。

好垃圾的做法，不过跑的还行

// 德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱
// 德丽莎的可爱在于德丽莎很可爱，德丽莎为什么很可爱呢，这是因为德丽莎很可爱！
// 没有力量的理想是戏言，没有理想的力量是空虚
#include <bits/stdc++.h>
#define LL long long
#define int long long 
using namespace std;
char ibuf[1 << 15], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, 1 << 15, stdin), p1==p2) ? EOF : *p1++)
inline int read() {
  char ch = getchar();  int x = 0, f = 1;
  while (ch < '0' || ch > '9')  {  if (ch == '-')  f = -1;  ch = getchar();  }
  while (ch >= '0' && ch <= '9')  x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
  return x * f;
}
void print(LL x) {
  if (x > 9)  print(x / 10);
  putchar(x % 10 + '0');
}
template<class T> bool chkmin(T &a, T b) { return a > b ? (a = b, true) : false; }
template<class T> bool chkmax(T &a, T b) { return a < b ? (a = b, true) : false; }
#define rep(i, l, r) for (int i = (l); i <= (r); i++)
#define repd(i, l, r) for (int i = (l); i >= (r); i--)
#define REP(i, l, r)  for (int i = (l); i < (r); i++)
const int N = 2e6, M = 2e5;
const int c1 = 300000, c2 = 4000, c3 = 500;
int n, tot, vib[N];
LL ans, now;
string a[M];
pair <string,int> pt[N];
map <string,int> mp, mp2, mp3, vis;
string get2(string s) {  string now;  now.clear();  now.push_back(s[4]);  now.push_back(s[5]);  return now;  }
string get4(string s) {  string now;  now.clear();  now.push_back(s[2]);  now.push_back(s[3]);  now.push_back(s[4]);  now.push_back(s[5]);  return now;  }
int id(string s2) {
  int sum = 0;
  for (int i = 0; i < s2.size(); i++)  sum = sum * 10 + (s2[i] - '0');
  return sum;
}
string idstring(int x) {
  string it;  it.clear();
  if (x <= 9)  it.push_back(0 + '0'), it.push_back(x + '0');
  else  it.push_back(x / 10 + '0'), it.push_back(x % 10 + '0');
  return it;
}
int y[N], x[N];
int gg;
void qwq1(string zz1, string zz2, string zz3) {
  // y x
  int pos = 0, q1 = -1;
  rep (i, 0, 99) {
    if (vib[i])  continue;
    if (y[i] > q1) {  q1 = y[i];  pos = i;  }
  }
  int gp = pos;
  vib[pos] = 1;
  now += 1ll * q1 * c2;
  pos = 0, q1 = -1;
  rep (i, 0, 99) {
    if (vib[i])  continue;
    if (x[i] > q1) {  q1 = x[i];  pos = i; }
  }
  now += 1ll * q1 * c1;
  vib[gp] = 0;
}
void qwq2(string zz1, string zz2, string zz3) {
  // x y
  int pos = 0, q1 = -1;
  rep (i, 0, 99) {
    if (vib[i])  continue;
    if (x[i] > q1) {  q1 = x[i];  pos = i;  }
  }
  int gp = pos;
  vib[pos] = 1;
  now += 1ll * q1 * c1;
  pos = 0;  q1 = -1;
  rep (i, 0, 99) {
    if (vib[i])  continue;
    if (y[i] > q1) {  q1 = y[i];  pos = i;  }
  }
  now += 1ll * q1 * c2;
  vib[gp] = 0;
}
void solve() {
  cin >> n;
  rep (i, 1, n)  cin >> a[i], mp[ a[i] ]++;
  rep (i, 1, n)  mp2[ get4(a[i]) ] ++, mp3[ get2(a[i]) ] ++;
  rep (i, 1, n) {
    if (!vis[get4(a[i])]) {
      ++tot;
      vis[get4(a[i])] = tot;
      pt[tot] = {a[i], 1};
    }  else {  int now = vis[get4(a[i])];  pt[now].second++;  }
  }
  rep (i, 1, tot) {
    string it = get2(pt[i].first);
    chkmax(y[id(it)], pt[i].second);
  }
  tot = 0;  vis.clear();
  rep (i, 1, n) {
    if (!vis[a[i]]) {
      ++tot;  
      vis[a[i]] = tot;
      pt[tot] = {a[i], 1};
    }  else {  int now = vis[a[i]];  pt[now].second ++;  }
  }
  rep (i, 1, tot) {
    string it = get2(pt[i].first);
    chkmax(x[id(it)], pt[i].second);
  }
  rep (z1, 0, 99) {
    rep (z2, z1 + 1, 99) {
      rep (z3, z2 + 1, 99) {
        now = 0;    
        string zz1, zz2, zz3;  zz1 = idstring(z1);  zz2 = idstring(z2);  zz3 = idstring(z3);
        now += 1ll * c3 * mp3[zz1];  now += 1ll * c3 * mp3[zz2];  now += 1ll * c3 * mp3[zz3];
        vib[z1] = 1;  vib[z2] = 1;  vib[z3] = 1;
        gg = now;
        qwq1(zz1, zz2, zz3);  chkmax(ans, now);  
        now = gg;
        qwq2(zz1, zz2, zz3);  chkmax(ans, now);
        vib[z1] = 0;  vib[z2] = 0;  vib[z3] = 0;
      }
    }
  }
  cout << ans << "\n";
  // cout << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s.\n";
}
// #define LOCAL_DEFINE
signed main () {
#ifdef LOCAL_DEFINE
  freopen("lottery.in", "r", stdin);
  freopen("lottery.out", "w", stdout);
#endif
  ios :: sync_with_stdio(0);  cin.tie(0), cout.tie(0);
  int T = 1;  while (T--)  solve();
#ifdef LOCAL_DEFINE
  cerr << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s.\n";
#endif
  return 0;
}
/*
300000 1
+ 8000 2
+ 1500 3

1500 / 500 = 3
07 45 Z 300 * 5 = 1500
4837 Y 4000 * 2 = 8000
382947 X 300000 * 1 = 300000
*/

T2 战斗

\(k \leq n \leq 500, 1 \leq a_i \leq 3000\)。

---

不难发现其实有 \((n - 1)!\) 种安排方案，每次都是取出一个空位，然后让这两边的人打一架。

这个实际是在划分子问题，因为两边的人在取出这个空格之前是不可能打过架的，于是直接联想到区间 dp。

一个非常自然的想法是设 \(dp_{l,r, k}\) 表示区间 \([l, r]\) 中活下来的人是 \(k\) 的概率。

然后接下来枚举中间的空格将区间分为 \([l, t], [t + 1, r]\)，然后还要枚举一下这两个区间种不包含 \(k\) 的那个区间的胜者是谁，然后直接合并就是了，复杂度 \(O(n^5)\)。

然后因为求区间 \([l, r]\) 的时候，\([l, t],[t + 1, r]\) 是互相独立的，只用求出各自的答案就好了。

考虑设立 \(f_{l, r}, g_{l, r}\) 分别表示区间 \([l, r]\) 打架最后 \(l, r\) 赢了的概率。

那么 \(dp_{l, r, k} = g_{k, r} \times f_{l, k}\)。

然后 \(f_{l, r}, g_{l, r}\) 的转移其实类似之前提到的 dp 转移，这里以 \(f_{l, r}\) 为例子。

首先需要枚举一下断点 \(k\) 把区间 \([l, r]\) 分成 \([l, k], [k + 1, r]\)，然后因为是要 \(l\) 赢，所以 \([l, k]\) 中肯定胜利的是 \(l\)，所以 \([l, k]\) 直接就是 \(f_{l, k}\) 就好了，但是对于 \([k + 1, r]\) 并不知道具体谁赢，于是枚举一下是 \(x\) 赢了，然后最后就是 \(f_{l, r} += f_{l, k} \times dp_{k + 1, r, x} \times p_{l, x}\)。

其中 \(p_{l, x}\) 表示 \(l\) 战胜 \(x\) 的概率，\(g\) 转移类似，这样复杂度为 \(n^4\)，并且常数很小！

接下来考虑神秘优化，\(dp_{l,r,k}\) 的转移复杂度正确的为 \(n^3\)，于是考虑优化 \(f,g\) 的转移，这里以 \(f\) 为例子。

\[f_{l, r} = \sum_{k=l}^{r-1} \sum_{x=k+1}^r f_{l, k} \times dp_{k + 1, r, x} \times p_{l, x} \times \dfrac{1}{r - l} \\ f_{l, r} = \dfrac{1}{r - l} \sum_{x = l + 1}^r \sum_{k = l} ^{x - 1} f_{l, k} \times dp_{k + 1, r, x} \times p_{l, x} \\ f_{l, r} = \dfrac{1}{r - l} \sum_{x = l + 1}^r \sum_{k = l} ^{x - 1} f_{l, k} \times g_{k + 1, x} \times f_{x, r} \times p_{l, x} \\ f_{l, r} = \dfrac{1}{r - l} \sum_{x = l + 1}^r f_{x, r} \times p_{l, x} \sum_{k = l}^{x - 1} f_{l, k} \times g_{k + 1, x} \]

然后设 \(h_{l, x}\) 表示 \(\sum_{k =l} ^ {x - 1} f_{l, k} \times g_{k + 1,x}\)。

每次转移的时候先预处理出 \(h\)，然后在做 \(f\) 的转移，就可以做到 \(n^3\)，\(g\) 同理。

于是总时间复杂度 \(n^3\)。

// 德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱
// 德丽莎的可爱在于德丽莎很可爱，德丽莎为什么很可爱呢，这是因为德丽莎很可爱！
// 没有力量的理想是戏言，没有理想的力量是空虚
#include <bits/stdc++.h>
#define LL long long
using namespace std;
char ibuf[1 << 15], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, 1 << 15, stdin), p1==p2) ? EOF : *p1++)
inline int read() {
  char ch = getchar();  int x = 0, f = 1;
  while (ch < '0' || ch > '9')  {  if (ch == '-')  f = -1;  ch = getchar();  }
  while (ch >= '0' && ch <= '9')  x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
  return x * f;
}
void print(LL x) {
  if (x > 9)  print(x / 10);
  putchar(x % 10 + '0');
}
template<class T> bool chkmin(T &a, T b) { return a > b ? (a = b, true) : false; }
template<class T> bool chkmax(T &a, T b) { return a < b ? (a = b, true) : false; }
#define rep(i, l, r) for (int i = (l); i <= (r); i++)
#define repd(i, l, r) for (int i = (l); i >= (r); i--)
#define REP(i, l, r)  for (int i = (l); i < (r); i++)
const int N = 600;
int n, k, a[N];
const double eps = 1e-8;
double dp[N][N][N], f[N][N], g[N][N], p[N][N], h[N][N], h2[N][N];
void solve() {
  n = read(), k = read();
  rep (i, 1, n)  a[i] = read();
  rep (i, 1, n)  f[i][i] = g[i][i] = dp[i][i][i] = 1.0;
  rep (i, 1, n) {
    rep (j, 1, n) {
      if (i == j)  continue;
      p[i][j] = ((double) (1.0 * a[i]) / (1.0 * a[i] + 1.0 * a[j]));
    }
  }
  rep (len, 2, n) {
    rep (l, 1, n) {
      int r = l + len - 1;
      if (r > n)  break;
      rep (x, l + 1, r) {
        if (h[l][x] > eps)  continue;
        rep (k, l, x - 1)  h[l][x] += f[l][k] * g[k + 1][x];
      }
      rep (x, l + 1, r)  f[l][r] += f[x][r] * p[l][x] * h[l][x];
      f[l][r] /= (r - l);
      rep (x, l, r - 1)  g[l][r] += g[l][x] * h[x][r] * p[r][x];
      g[l][r] /= (r - l);
      rep (k, l, r)  dp[l][r][k] = g[l][k] * f[k][r];
    }
  }
  printf("%.10lf\n", dp[1][n][k]);
}
signed main () {
#ifdef LOCAL_DEFINE
  freopen("1.in", "r", stdin);
  freopen("1.ans", "w", stdout);
#endif
  int T = 1;  while (T--)  solve();
#ifdef LOCAL_DEFINE
  cerr << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s.\n";
#endif
  return 0;
}

T3 扑克

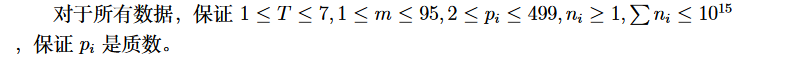
注意到，貌似不能选太多的数质数相乘，否则就会太大了，就算剩下的全部加起来都够不了。

只能抽出 \((\log n + \log p)\) 个质数相乘。

那么剩下的质数的和其实没有太多的情况，无脑枚举剩下质数的和，然后判断一下是否能够被凑出来。

代码比讲的清楚。

// 德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱
// 德丽莎的可爱在于德丽莎很可爱，德丽莎为什么很可爱呢，这是因为德丽莎很可爱！
// 没有力量的理想是戏言，没有理想的力量是空虚
#include <bits/stdc++.h>
#define LL long long
#define int long long
using namespace std;
char ibuf[1 << 15], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, 1 << 15, stdin), p1==p2) ? EOF : *p1++)
inline int read() {
  char ch = getchar();  int x = 0, f = 1;
  while (ch < '0' || ch > '9')  {  if (ch == '-')  f = -1;  ch = getchar();  }
  while (ch >= '0' && ch <= '9')  x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
  return x * f;
}
void print(LL x) {
  if (x > 9)  print(x / 10);
  putchar(x % 10 + '0');
}
template<class T> bool chkmin(T &a, T b) { return a > b ? (a = b, true) : false; }
template<class T> bool chkmax(T &a, T b) { return a < b ? (a = b, true) : false; }
#define rep(i, l, r) for (int i = (l); i <= (r); i++)
#define repd(i, l, r) for (int i = (l); i >= (r); i--)
#define REP(i, l, r)  for (int i = (l); i < (r); i++)
const int N = 300;
int m, b[N], num, id[N], ans;
pair <int,int> a[N];
void dfs(int x) {
  if (x == num + 1) {
    int sum1 = 0;
    rep (i, 1, num)  sum1 += b[i];
    int v1 = 0, v2 = 1;
    rep (i, 1, num) {
      if (id[i] == 1)  v1 += b[i];
      else {
        v2 *= b[i];
        if (v2 > sum1)  return;
      }
    }
    if (v1 == v2)  ans = max(ans, v1);
    return;
  }
  id[x] = 1;  dfs(x + 1);
  id[x] = 0;  dfs(x + 1);
}
void solve() {
  m = read();
  int sum = 0;
  rep (i, 1, m)  a[i].first = read(), a[i].second = read(), sum += a[i].second;
  if (sum <= 10) {
    num = 0;  ans = 0;
    rep (i, 1, m) 
      rep (j, 1, a[i].second)  b[++num] = a[i].first;
    dfs(1);
    printf("%lld\n", ans);
    return;
  }
  int now = 0;
  rep (i, 1, m)  now += a[i].first * a[i].second;
  int ans = 0;
  repd (vv, now, max(1ll, now - 10000)) {
    int nowq = now, fl = 0;
    int nowg = 1, nowt = vv;
    rep (i, 1, m) {
      int x = a[i].first, y = a[i].second, cnt = 0;
      while (nowt % x == 0) {
        nowt /= x;
        cnt++;
        nowg *= x;  nowq -= x;
      }
      if (cnt > y) { fl = 1;  break;  } 
    }
    if (fl)  continue;
    if (nowg == vv && nowq == vv) {  ans = vv;  break;  }
  }
  printf("%lld\n", ans);
  // cout << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s.\n";
}
// #define LOCAL_DEFINE
signed main () {
#ifdef LOCAL_DEFINE
  freopen("poker.in", "r", stdin);
  freopen("poker.out", "w", stdout);
#endif
  int T = read();  while (T--)  solve();
#ifdef LOCAL_DEFINE
  cerr << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s.\n";
#endif
  return 0;
}

T4 排队

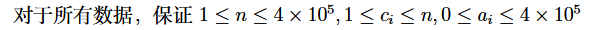
有一个 \(\log\) 的做法，但是我考场没想到，首先你考虑暴力咋写，其实就是找到一个区间内某个数的第一个出现的位置。

然后你暴力找很慢，空间又给了 \(1G\)，然后你就发现可以写个块状链表，对每块在维护一个桶，然后每次直接暴力从前面的块开始往后面找，找到第一个出现的位置就返回，然后暴力插入就好了。

\(4e5\) 根号 \(2s\) 有梦想就能过，块长取的 \(1000\)。

// 德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱
// 德丽莎的可爱在于德丽莎很可爱，德丽莎为什么很可爱呢，这是因为德丽莎很可爱！
// 没有力量的理想是戏言，没有理想的力量是空虚
#include <bits/stdc++.h>
#define LL long long
using namespace std;
char ibuf[1 << 15], *p1, *p2;
#define getchar() (p1 == p2 && (p2 = (p1 = ibuf) + fread(ibuf, 1, 1 << 15, stdin), p1==p2) ? EOF : *p1++)
inline int read() {
  char ch = getchar();  int x = 0, f = 1;
  while (ch < '0' || ch > '9')  {  if (ch == '-')  f = -1;  ch = getchar();  }
  while (ch >= '0' && ch <= '9')  x = (x << 1) + (x << 3) + (ch ^ 48), ch = getchar();
  return x * f;
}
void print(LL x) {
  if (x > 9)  print(x / 10);
  putchar(x % 10 + '0');
}
template<class T> bool chkmin(T &a, T b) { return a > b ? (a = b, true) : false; }
template<class T> bool chkmax(T &a, T b) { return a < b ? (a = b, true) : false; }
#define rep(i, l, r) for (int i = (l); i <= (r); i++)
#define repd(i, l, r) for (int i = (l); i >= (r); i--)
#define REP(i, l, r)  for (int i = (l); i < (r); i++)
const int N = 4e5 + 5, blk = 1000, K = (N - 1) / blk + 1;
int col[N], a[N], n, q;
int fr[K][N];
deque <int> dq[K];
int get(int x) {  return col[dq[x / blk][x % blk]];  }
int find(int x,int mn) {
  int mx = n / blk, c = col[x];
  if (mn && get(mn - 1) == c)  return mn;
  for (int i = mn / blk; i <= mx; i++) {
    if (fr[i][c] == 0)  continue;
    int pos = i * blk;
    for (auto x : dq[i]) {
      if (pos >= mn && col[x] == c)  return pos;
      pos++;
    }
  }
  return n;
}
void insert(int i, int x) {
  int now = i / blk, pos = i % blk, c = col[x];
  dq[now].insert(dq[now].begin() + pos, x);
  fr[now][c]++;
  while (dq[now].size() > blk) {
    int to = dq[now].back();  dq[now].pop_back();  fr[now][col[to]]--;
    dq[now + 1].push_front(to);  fr[now + 1][col[to]]++;
    now++;
  }
  n++;
}
void solve() {
  q = read();
  rep (i, 1, q)  col[i] = read(), a[i] = read();
  rep (i, 1, q) {
    int pos = find(i, max(0, i - a[i] - 1));
    insert(pos, i);
  }
  // cout << "qwqw\n";
  int it = 0;
  while (dq[it].size()) {
    for (auto to : dq[it])  printf("%d ", to);
    it++;
  }
}
// #define LOCAL_DEFINE
signed main () {
#ifdef LOCAL_DEFINE
  freopen("queue.in", "r", stdin);
  freopen("queue.out", "w", stdout);
#endif
  int T = 1;  while (T--)  solve();
#ifdef LOCAL_DEFINE
  cerr << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s.\n";
#endif
  return 0;
}