SA 代替 SAM 的 parent 树
\(\mathscr{A.}\) 前言

\(\mathscr{B.}\) 内容
SA 其实可以构建出一个 sam 的 parent tree。
考虑设 \(\text{beginpos(t)}\) 表示字符串 \(s\) 的子串 \(t\) 在 \(s\) 中所有的其实位置所构成的集合。
qwqqaqqwq 中 wq 的 \(\text{beginpos}\) 也就是 \(\{2,8\}\)。
然后所有 \(t\) 都可以根据 \(\text{beginpos(t)}\) 被划分成为若干个等价类。
然后,你思考一下,你发现这东西不就是 SAM 的反串的 \(\text{endpos}\) 吗。
那我们知道 SAM 的 \(\text{endpos}\) 的本质不同的等价类数量为 \(O(n)\)。
那么考虑使用 SA 来求解这个过程?
我们知道每个等价类在 sa 数组上都一定会对应一个区间。
这个很显然把。
举个例子,字符串 \(\text{aabaaab}\) 后缀排序后如下:
那么对于一个 \(\text{beginpos(aab)}\) 来说,他在 sa 数组中出现于 \(\{3,4\}\) 。
因为是同一段相同的字符串,而在后缀排序中,字典序排序,所以的话,对于一个串 \(t\) 来说,在 sa数组上包含他的一定是一段连续的区间。
那么也就是 \(\text{beginpos(t)}\) 在 sa 数组上一定是一段连续的区间。
联想 sam,sam 的建立与 parent 树是分不开关系的。
我们发现,对于一个等价类,parent 树中要求了子树被包含。
那如果我们我们之前所所说的哪些等价类关系弄成一个树,是不是就好了/se。
根据人类智慧,我们对字符串的 height 数组建立笛卡尔树,然后将原串的后缀作为叶子节点。
我们发现,这就是一颗可以实现 SAM 功能的树了。
还是举个例子,仍然是字符串 \(\text{aabaaab}\)。
建立出来,应该是长下面这个样子。
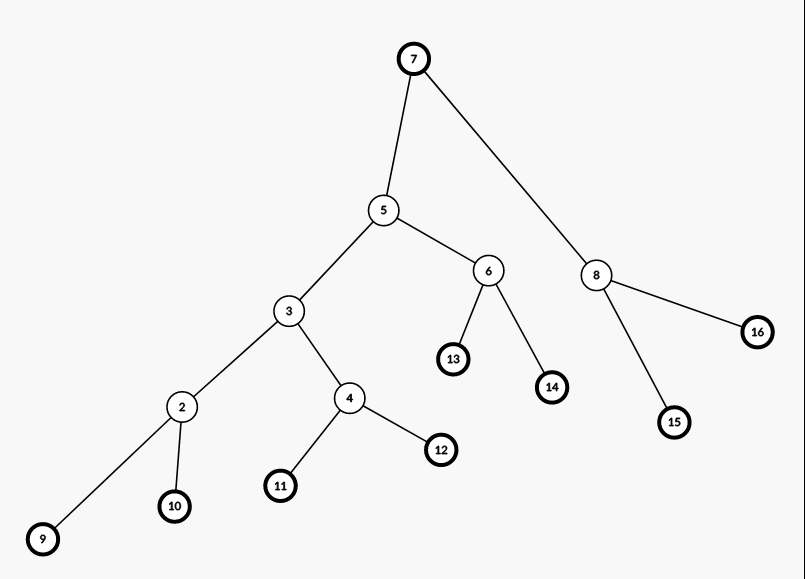
最下面的一层就是 sa 数组。
然后,就完成了,而且还有很多优美的性质。
对于任意两个叶子节点,他们的 lca 就是他们的 lcp。
每个等价类在这颗树上面都对应一个子树,也对应了一个 sa 上的区间。
其次,这个数的先序遍历结果就是后缀数组。
然后我们发现这个可以实现 sam 的 parent tree 的相同功能。
那么对于 sam 的模板题,我们需要注意到性质,对于这个笛卡尔树 \(2 \sim n\) 的节点,他的子树中有的 \(n + 1 \sim 2n\) 的节点个数就是他当前代表的字符串的出现次数。
而他有一个权值 val 为 height 所以他代表的字符串就是这一段区间中的 lcp。
然后对这个取 max 即可,可以看代码。
当然没啥大用,就一个 parent tree,还是 sam 好,虽然我还没咋写过。
// 德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱德丽莎你好可爱
// 德丽莎的可爱在于德丽莎很可爱,德丽莎为什么很可爱呢,这是因为德丽莎很可爱!
#include <bits/stdc++.h>
#define int long long
using namespace std;
#define FOR(i, l, r) for(int i = (l); i <= r; ++i)
#define REP(i, l, r) for(int i = (l); i < r; ++i)
#define DFR(i, l, r) for(int i = (l); i >= r; --i)
#define DRP(i, l, r) for(int i = (l); i > r; --i)
#define FORV(i, ver) for(int i = 0; i < ver.size(); i++)
#define FORP(i, ver) for(auto i : ver)
template<class T>T wmin(const T &a, const T &b) {return a < b ? a : b;}
template<class T>T wmax(const T &a, const T &b) {return a > b ? a : b;}
template<class T>bool chkmin(T &a, const T &b) {return a > b ? a = b, 1 : 0;}
template<class T>bool chkmax(T &a, const T &b) {return a < b ? a = b, 1 : 0;}
inline int read() {
int x = 0, f = 1; char ch = getchar();
while( !isdigit(ch) ) { if(ch == '-') f = -1; ch = getchar(); }
while( isdigit(ch) ) { x = (x << 1) + (x << 3) + (ch ^ 48); ch = getchar(); }
return x * f;
}
const int N = 3e6;
int n, num = 200, f1[N], f2[N], sa[N], tong[N], height[N];
char ch[N];
void SA() {
FOR(i, 1, num) tong[i] = 0; FOR(i, 1, n) ++tong[ f1[i] = ch[i] ];
FOR(i, 1, num) tong[i] += tong[i - 1]; DFR(i, n, 1) sa[ tong[f1[i]]-- ] = i;
for(int l = 1; l <= n; l <<= 1) { int cnt = 0;
FOR(i, n - l + 1, n) f2[++cnt] = i; FOR(i, 1, n) if(sa[i] > l) f2[++cnt] = sa[i] - l;
FOR(i, 1, num) tong[i] = 0; FOR(i, 1, n) ++tong[f1[i]]; FOR(i, 1, num) tong[i] += tong[i - 1];
DFR(i, n, 1) sa[ tong[ f1[ f2[i] ] ] -- ] = f2[i], f2[i] = 0; swap(f1, f2);
f1[ sa[1] ] = 1; cnt = 1;
FOR(i, 2, n) f1[ sa[i] ] = ( f2[ sa[i] ] == f2[ sa[i - 1] ] && f2[ sa[i] + l ] == f2[ sa[i - 1] + l] ) ? cnt : ++cnt;
if(cnt == n) break; num = cnt;
}
}
void Getheight() {
int k = 0; FOR(i, 1, n) {
if(k) k--; int j = sa[f1[i] - 1];
while (ch[i + k] == ch[j + k]) k++; height[ f1[i] ] = k;
}
}
int ls[N], rs[N], s[N], tp, fa[N], rt, val[N];
void build() {
if(n == 1) { rt = 2; return; }
ls[2] = n + 1; rs[2] = n + 2;
fa[ ls[2] ] = fa[ rs[2] ] = rt = s[++tp] = 2;
FOR (i, 3, n) {
while (tp && height[ s[tp] ] > height[i] ) tp--;
if ( tp ) ls[i] = rs[ s[tp] ], fa[ rs[ s[tp] ] ] = i, rs[ s[tp] ] = i, fa[i] = s[tp];
else ls[i] = rt, fa[rt] = i, rt = i;
rs[i] = n + i, fa[ rs[i] ] = i, s[++tp] = i;
}
FOR (i, 2, n) val[i] = height[i];
}
int siz[N];
void dfs(int u) {
if ( !u ) return;
if (u > n) siz[u] = 1;
dfs(ls[u]), dfs(rs[u]);
siz[u] += siz[ ls[u] ]; siz[u] += siz[ rs[u] ] ;
}
signed main () {
scanf("%s", ch + 1); n = strlen(ch + 1);
SA(); Getheight();
build(); dfs(rt);
int ans = 0;
FOR(i, 2, n) if(siz[i] > 1) ans = wmax( ans, siz[i] * val[i] );
cout << ans << "\n";
return 0;
}
//ans = 8
\(\mathscr{C.}\) 参考资料
洛谷P6292中RPChe_大佬的题解https://www.luogu.com.cn/blog/Darth-Che/solution-p6292
论文Suffix Arrays-A Linear-Time Algorithm


 浙公网安备 33010602011771号
浙公网安备 33010602011771号