dp 优化入门

蒟蒻学了这个忘了那个，学了那个忘了这个，于是开篇博客总结一下 QwQ

不过等我 github 博客弄好了就不会在这里更新了

\(\texttt{斜率优化}\)

题目描述：\(n\) 个玩具，第 \(i\) 个玩具长度为 \(c_i\)，要求将玩具分成若干段，定义一段 \([l,r]\) 的权值 \(L\) 为 \(r-l + \sum_{k=l}^rc_k\)。一段长为 \(x\) 的段的费用为 \((x-L)^2\)，其中 \(L\) 为给定的一个常数，要求最小化分段后的费用。

考虑设计暴力 \(\texttt{dp}\) ： \(f_i\) 表示以 \(i\) 结尾，分成若干段得到的最小总费用。

设立 \(s_k\) 表示 \(\sum_{i=1}^k c_i\)

\[f_i=\min_{j=1}^{i-1}f_j+(i-j + s_i - s_{j-1} - L)^2 \]

这是暴力的平方方程，我们考虑将所有 \(c_i\) 都在一开始减去 \(1\)，那么就可以省略掉 \(i-j\)，变为：

\[f_i=\min_{j=1}^{i-1}f_j+\{ s_i - s_{j-1} - (L + 1)\}^2 \]

再让 \(L + 1\)，变为：

\[f_i=\min_{j=1}^{i-1}f_j+( s_i - s_{j-1} - L)^2 \]

好看多了，暴力拆开平方项。

\[f_i=\min_{j=1}^{i-1}\{ f_j+ s_i^2+s_{j-1}^2-2s_is_{j-1}+L^2-2Ls_i+2Ls_{j-1}\} \]

先去掉 \(\min\)，然后考虑两个决策点 \(j_1,j_2\) 如果 \(j_2\) 比 \(j_1\) 更优，那么需要满足什么条件。

\[f_i= f_j+ s_i^2+s_{j-1}^2-2s_is_{j-1}+L^2-2Ls_i+2Ls_{j-1} \]

也就是什么时候：

\[f_{j_1}+ s_i^2+s_{j_1-1}^2-2s_is_{j_1-1}+L^2-2Ls_i+2Ls_{j_1-1}<f_{j_2}+ s_i^2+s_{j_2-1}^2-2s_is_{j_2-1}+L^2-2Ls_i+2Ls_{j_2-1} \]

考虑消去同类项，剩下的只有：

\[f_{j_1}+s_{j_1-1}^2-2s_is_{j_1-1}+2Ls_{j_1-1}<f_{j_2}+s_{j_2-1}^2-2s_is_{j_2-1}+2Ls_{j_2-1} \]

考虑进行参变量分离，让一边只有 \(i\) 这种定项，另一边则是不定项，那么得到的答案是：

\[2s_i(s_{j_2-1-s_{j_1-1}})<f_{j_2}+s_{j_2-1}^2+2Ls_{j_2-1}-(f_{j_1}+s_{j_1-1}^2+2Ls_{j_1-1}) \]

然后除过去：

\[2s_i<\dfrac{f_{j_2}+s_{j_2-1}^2+2Ls_{j_2-1}-(f_{j_1}+s_{j_1-1}^2+2Ls_{j_1-1})}{(s_{j_2-1-s_{j_1-1}})} \]

令 \(X(j) = s_{j-1}\)， \(Y(j) = f_{j}+s_{j-1}^2+2Ls_{j-1}\) ，写成代数关系抽象。

那么原式子化为 \(2s_i<\dfrac{Y(j_2)-Y(j_1)}{X(j_2)-X(j_1)}\) ，你发现这就是斜率，于是对于这道题目。按照这个，使用单调队列维护单增的决策点即可。

这就是从代数的层面上理解的斜率优化。

还有些内容先咕咕一下。

wqs 二分

刚刚把这东西弄懂，可能需要记录一下。

考虑这么一个问题：

将一个长为 \(n\) 非负整数序列分为 \(k\) 段，每段权值为段内元素和的平方，要求最小化权值。

首先，如果没有 \(k\) 段限制，最终整个序列一定会被划分为 \(n\) 段，因为都为非负整数，两个非负整数 \(a,b\) 满足 \((a+b)^2>a^2+b^2\) 。

但是有了这个之后，我们就只会写一个 \(O(nk)\) 的暴力了。

然后神仙 wqs 就整理出了这么一个二分方法 %%%%%

考虑 \(f_{i,j}\) 表示前 \(i\) 个数分成 \(j\) 段的最小权值。

然后令 \(F_i\) 表示 \(f_{n,i}\)。

通过一开始的结论，你发现 \(F_i\) 一定是一段凸函数，类似下面这种。

在这个题中，这是一个下凸函数，也就是斜率单调不增。

其中的 \(x\) 表示的是分段数量，然后 \(y\) 表示的是对应取到的值。

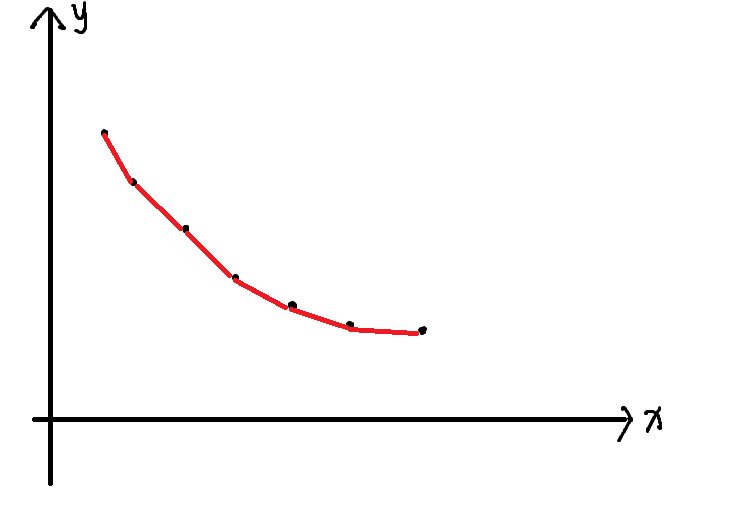
我们发现，如果我们现在有一个斜率为 \(k\) 的直线，那么拿这个直线去和这个凸包相切的话，我们会得到一个点 \((p,F_p)\) 。

这个点就是在斜率为 \(k\) 的情况下，所有点中，纵截距最小的那个。（因为这里是下凸包，如果是上凸包就是最大的）

也就是在所有点 \((i,F_i)\) 中，使得 \(F_i - ki\) 最小的那个点 \(p\)。

那就考虑列出这个截距的函数，你不难发现这个截距也是一个下凸函数。

一个下凸函数加上一个一次函数后，仍然会是一个下凸函数。

证明比较显然（），考虑如果加入的一次函数斜率 \(<0\) 那么理所应当，如果 \(>0\) ，那么就是左小右大，这个时候函数斜率变成了负的，所以还是在变小。

那么接下来的问题是我们如何在确定 \(k\) 的时候求出 \(p\) 和对应的 \(F_p\)。根据他的截距最小，本问题可以化归为：

每个物品的代价减去 \(k\)，本题也就是每次选一段就将答案减去 \(k\)。

然后求出在不限段数的情况下,答案的最小值 \(g\) 以及取到最小值时的段数 \(p\) ，那么求出 \(F_p= g+pk\) ，本题用一个斜率优化 dp 就搞完了。

这样为啥可以呢（），感觉很感性，就是你思考你给每段赋值了一个额外权值，我们现在要最小化权值，当额外权值大的时候，你就会尽可能分少段，当额外权值小的时候，你就会可能会分多段。

假设取得最小值的时候为 \(m\)，如果这个时候 \(p=m\) 那就已经取到了最小值。

如果 \(p < m\) 那么说明我们的斜率还不够小，如果 \(p>m\) 的时候说明我们的斜率还不够大，如果是上凸包就会改变大小关系。

但是注意一个很坑人的地方，，，

我们其实有可能找不到这个 \(m\) ，就是如果有三点共线了。

那么我中间的点就不会被取到了

也可以解决，可以由他左边这个点

然后这就是 wqs 二分的全过程 QwQ，感觉确实很强，不过上面的理性证明我也不是很会，不过大概能悟道是这么个理。