1. n阶行列式定义
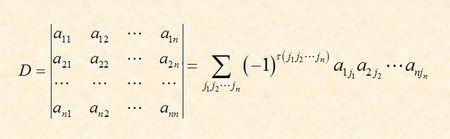
τ为逆序数。
2.行列式可以等同于多维空间向量,由此可以推导出它的性质
行列式的行和列是等价的,行的性质也是列的性质
3.余子式
代数余子式有符号(“可以进行代数运算的余子式”)
可以通过代数余子式简化计算
行列式某行分别乘另外一行元素的代数余子式再求和,结果为0
4.重要行列式
上下三角形=∏aii;副对角线行列式=(-1)n(n-1)/2∏aii;
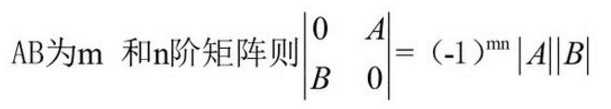
若AB为\方向,则不加(-1)mn;
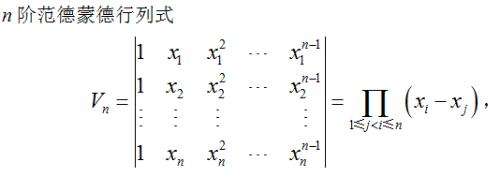
5.爪形行列式可以化为三角形
6.行列式每行元素之和相等时,可以将各列加到第一行,再提出公因式
7.不易利用已有性质的行列式可以考虑升一阶,即加边法
8.证明可用第一第二数学归纳法
9.代数余子式可以逆用
10.克拉默法则通过行列式运算求解线性方程组
11.行列式等于0有充要条件:
1.Ax=0;
2.A不可逆;
3.A有0特征值;
4.齐次线性方程组有非0解



