loj6677. EntropyIncreaser 与菱形计数

题意

略。

题解

很显然这个题目中的图在疯狂暗示，应该考虑的对应的三维问题。
这个三维问题就是在一个墙角堆石子，计算本质不同的方案数。
但是这个也是不太好做的问题。
接下去的这一步非常的巧妙，即将这个问题再转化为一个二维问题，即：
从右上角的所有格子往左下角的所有格子对应着走，且不相交的方案数。
怎么转化的呢？具体的如下：




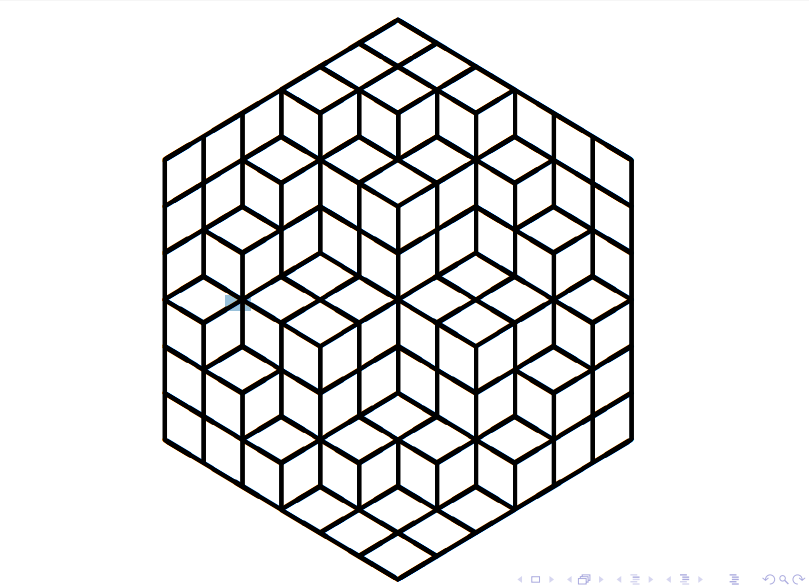
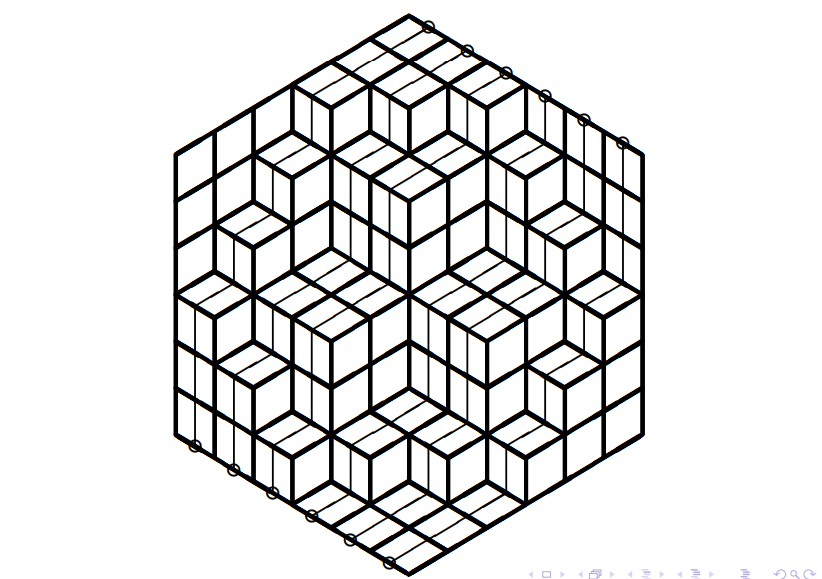
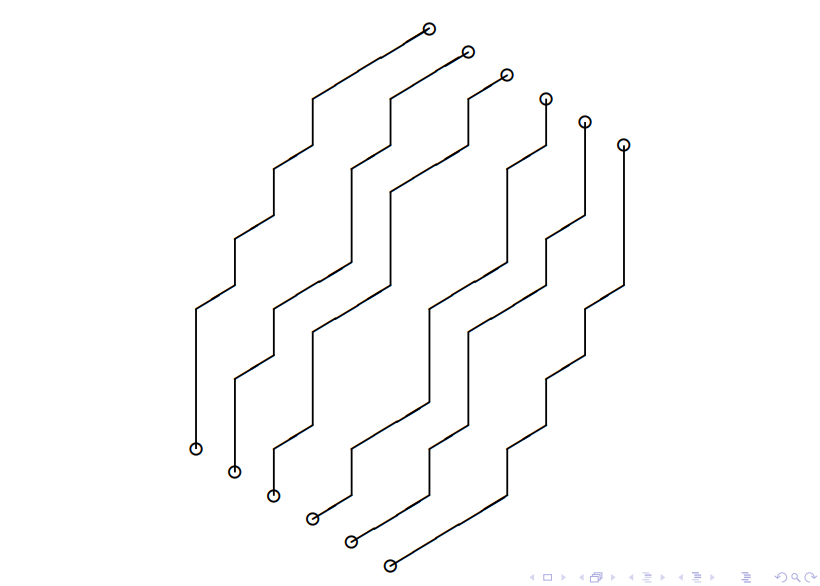
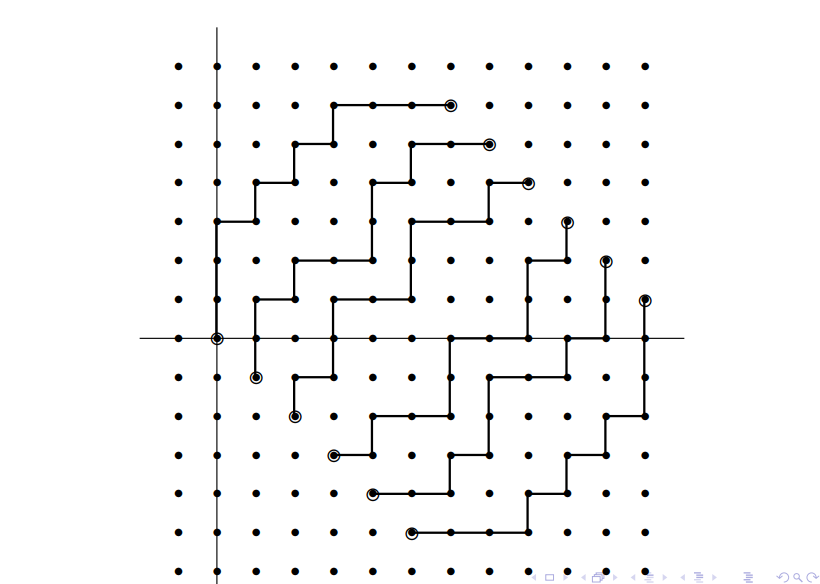
仔细观察一下，发现题目可以转化为在一个二维平面上，有两个大小相同的点集，求：
在两个点集建立间点对映射，对应点对之间通过一条二维非降路径相连，求不交路径组的总方案数。
这个问题很经典，有个Lindström–Gessel–Viennot lemma 定理就是专门求解这个问题的。
简单说，这个定理，即
对于一张无边权的DAG，给定\(n\)个起点和对应的\(n\)个终点（互不相同），这\(n\)条不相交路径的方案数为

\[\left| \begin{array} e(a_1, b_1) & e(a_1, b_2) & \cdots & e(a_1, b_n) \\ e(a_2, b_1) & e(a_2, b_2) & \cdots & e(a_2, b_n) \\ \vdots & \vdots & \ddots & \vdots \\ e(a_n, b_1) & e(a_n, b_2) & \cdots & e(a_n, b_n) \\ \end{array} \right| \]

（行列式）
其中\(e(a,b)\)为图上\(a\)到\(b\)的方案数。
具体证明，大概口胡一下，就是在一个相交的方案中，必然存在两条路径相交在一个点。找到最后那个交点，找到交于此点的两条路径（有可能多于两条），将他们的起点互换，贡献在行列式中即可抵消。
即下图中此情况：

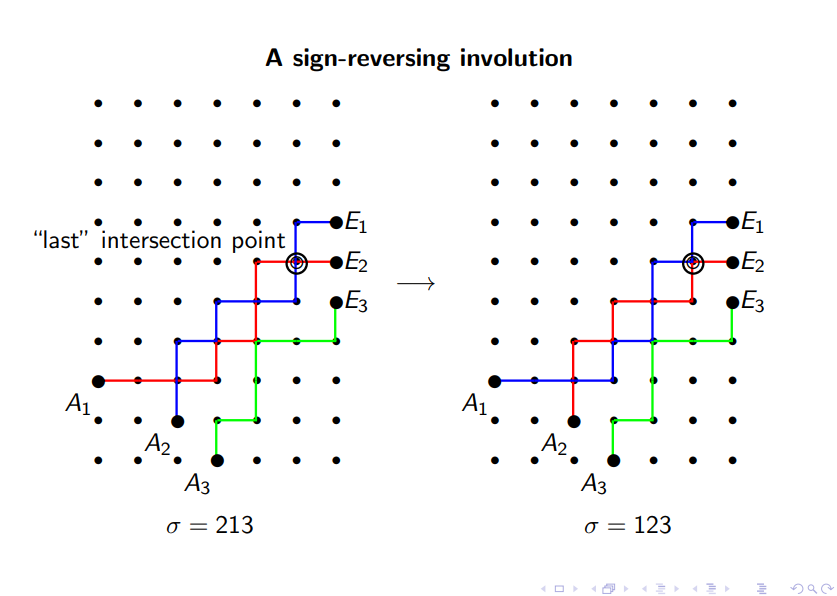
严谨的证明没有证过。
然后对于这道题，答案即为：

\[\left| \begin{array} e(s_1, t_1) & e(s_1, t_2) & \cdots & e(s_1, t_n) \\ e(s_2, t_1) & e(s_2, t_2) & \cdots & e(s_2, t_n) \\ \vdots & \vdots & \ddots & \vdots \\ e(s_n, t_1) & e(s_n, t_2) & \cdots & e(s_n, t_n) \\ \end{array} \right| \]

求\(e(s_i, t_j)\)，其中可以令\(s_i(a + i - 1, b - i + 1), t_j(j - 1, -j + 1)\)，则

\[e(s_i, t_j) = \binom{(a + i - 1 + b - i + 1) + (j - 1 - j + 1)}{(a + i - 1) + (j - 1)} = \binom{a + b}{a + i + j - 2} \]

最后一步不会，即这上面的东西最后就是

\[\prod_{i = 1} ^ a \prod_{j = 1} ^ b \prod_{k = 1} ^ c \frac{i + j + k - 1}{i + j + k - 2} \]

再随便推一步就好了。
复杂度\(\mathcal O(n \log p)\)。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 3e6 + 3, mod = 998244353;
int a, b, c; ll ans, tmp1, tmp2;
int fac[N], ivf[N];
int power (int a, int b) {
	int ret = 1;
	for ( ; b; b >>= 1, a = 1ll * a * a % mod) {
		if (b & 1) {
			ret = 1ll * ret * a % mod;
		}
	}
	return ret;
}
int main () {
	cin >> a >> b >> c;
	fac[0] = ivf[0] = 1;
	for (int i = 1; i < N; ++i) {
		fac[i] = 1ll * fac[i - 1] * i % mod;
	}
	ivf[N - 1] = power(fac[N - 1], mod - 2);
	for (int i = N - 2; i; --i) {
		ivf[i] = 1ll * ivf[i + 1] * (i + 1) % mod;
	}
	ans = 1;
	for (int i = 1; i <= a; ++i) {
		tmp1 = 1ll * fac[i + b + c - 1] * ivf[i + c - 1] % mod;
		tmp2 = 1ll * fac[i + b - 1] * ivf[i - 1] % mod;
		ans = 1ll * tmp1 * power(tmp2, mod - 2) % mod * ans % mod;
	}
	cout << ans << endl;
	return 0;
}