hdu 2073 无限的路

无限的路

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 7691    Accepted Submission(s): 3970

Problem Description

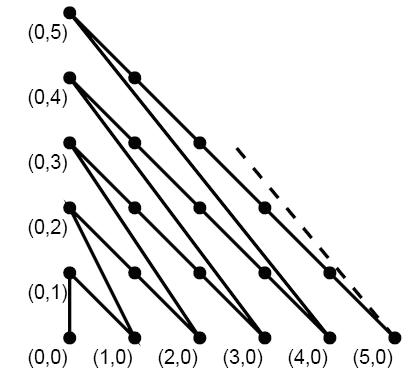
甜甜从小就喜欢画图画，最近他买了一支智能画笔，由于刚刚接触，所以甜甜只会用它来画直线，于是他就在平面直角坐标系中画出如下的图形：



甜甜的好朋友蜜蜜发现上面的图还是有点规则的，于是他问甜甜：在你画的图中，我给你两个点，请你算一算连接两点的折线长度（即沿折线走的路线长度）吧。

 

 

Input

第一个数是正整数N（≤100）。代表数据的组数。
每组数据由四个非负整数组成x1，y1，x2，y2；所有的数都不会大于100。

 

 

Output

对于每组数据，输出两点(x1,y1),(x2,y2)之间的折线距离。注意输出结果精确到小数点后3位。

 

 

Sample Input

5

0 0 0 1

0 0 1 0

2 3 3 1

99 99 9 9

5 5 5 5

 

 

Sample Output

1.000

2.414

10.646

54985.047

0.000

 

 

Author

Lily

 

 

Source

浙江工业大学网络选拔赛

 

 

又是一道递推题，独立完全找不到规律。。好烦好烦，还是看了别人的代码。

分析：这个线段距离原点的长可分为两部分。第一部分是无点的线段，长度依次为√（0^2+1^2）、√（1^2+2^2)、√（2^2+3^2）……√（(n-1)^2+n^2）这个n的值刚好为这一点的横纵坐标之和；第二部分是有点的线段，这个很容易发现长度依次为√2、2√2、3√2、……(m-1）√2 ，第m条有点线段长度是这一点横坐标乘以√2.并且这个m的值与n相等.

      综上，只需要求出两个点距离原点的距离，相减求绝对值即可。

 

题意：中文题，很好理解。

 

附上代码：

 

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
int abs(int a)
{
    return a>0?a:-a;
}
double xx(int x,int y)
{
    double ans;
    double m=(double)sqrt(2);
    int n,i;
    n=x+y;
    ans=0.0;
    for(i=1; i<n; i++)
        ans+=i*m;
    ans+=x*m;
    for(i=0; i<n; i++)
        ans+=sqrt(i*i+(i+1)*(i+1));
    return ans;
}

int main()
{
    int a1,b1,a2,b2,i,j,n,m;
    scanf("%d",&n);
    while(n--)
    {
        scanf("%d%d%d%d",&a1,&b1,&a2,&b2);
        printf("%.3lf\n",abs(xx(a2,b2)-xx(a1,b1)));
    }
    return 0;
}