poj 1920 Towers of Hanoi

Towers of Hanoi

Time Limit: 3000MS		Memory Limit: 16000K
Total Submissions: 2213		Accepted: 986
Case Time Limit: 1000MS

Description

Surely you have already come across the Towers of Hanoi problem: Wooden disks of different sizes are stacked on three pegs, and initially, all disks are stacked on the same peg sorted by size, with the largest disk at the bottom. The objective is to transfer the entire tower to one of the other pegs, moving only one disk at a time and never putting a larger disk onto a smaller one. 
According to an old myth, the monks at an ancient Tibetian monastery have been trying to solve an especially large instance of this problem with 47 disks for thousands of years. Since this requires at least 2⁴⁷ - 1 moves and the monks started out without a strategy, they messed it all up while still following the rules. Now they would like to have the disks stacked up neatly on any arbitrary peg using the minimum number of moves. But they all took a vow which forbids them to move the disks contrary to the rules. They want to know on which peg they should best stack the disks, and the minimum number of moves needed. 
Write a program that solves this problem for the monks. Your program should also be able to handle any number N (0 < N <= 100 000) of disks. The numbers involved in the computation can become quite large. Because of that, the monks are only interested in the number of moves modulo 1 000 000. 
Example 
The following example can be solved in four moves. 

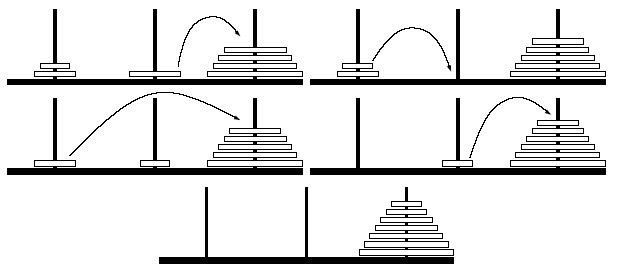
Input

The first line of the input file hanoi.in consists of the number N (N <= 100000) of disks. The second line consists of three integers s1, s2, s3 with 0 <= s1, s2, s3 <= N and s1+s2+s3 = N, the number of disks on each of the three pegs. Lines three to five each contain the sizes of the disks for one peg. More precisely: 
The (i + 2)-th line of the input file consists of integer numbers m_i,1 . . .m_i,si with 1 <= m_i,j <= N, the sizes of the disks on peg i. The disks are given from bottom to top, thus m_i,1 > m_i,2 > . . . > m_i,si . 
Note that an empty stack is given by an empty line. The set of N disks have different sizes. All numbers are separated by a single space.

Output

The first line of the output file hanoi.out consists of the number d in {1, 2, 3} of the peg onto which the disks can be stacked using the minimum number of moves. The second line consists of the number M of required moves modulo 1 000 000.

Sample Input

7
2 1 4
2 1
3
7 6 5 4

Sample Output

3
4

Source

CEOI 2003

 

用了汉诺塔的非递归算法，如果有n块要全部移动到C上的话，就需移动2^n-1，这是最基本的汉诺塔求解问题。再来看这一题，他要求我们把其中一个状态移动到一座塔上，其实也就是把一座塔移动到当前状态就好了，去画一下就知道又变成了基本的汉诺塔问题了。注意：最大的那块是不动的，从公式可以看出。

 

题意：给定一个汉诺塔的局面，问最少多少步可以将它们并到一个柱子上。

第一行n，表示n个盘子接下来一行3个数字m[i]，表示柱子上分别有几个盘子随后的三行每行m[i]个数字，表示在该柱子上的盘子的编号

第一行输出一个数字表示集中到哪个柱子上，第二行输出一个数字表示最小步数模1000000

 

附上代码：

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int main()
{
    int T,i,j,n,m;
    int a[5],b[100005],c[100005];
    while(~scanf("%d",&T))
    {
        for(i=1; i<=3; i++)
            scanf("%d",&a[i]);
        for(i=1; i<=3; i++)
        {
            for(j=1; j<=a[i]; j++)
            {
                scanf("%d",&n);
                b[n]=i;             //记录每个盘子所在的柱子位置
            }
        }
        c[0]=1;
        for(i=0; i<T; i++)
            c[i+1]=(c[i]*2)%1000000;   
        int s1=b[T],s2=b[T-1],s=0;   //s1为最大的盘子位置，s2为第二大的盘子位置
        for(i=T-1; i>0; i--,s2=b[i])
        {
            if(s1!=s2)   //假如盘子不在正确的位置上，将其移动
            {
                s=(s+c[i-1])%1000000;
                s1=6-s1-s2;     //记录剩余盘子新的位置
            }
        }
        printf("%d\n%d\n",b[T],s);
    }
    return 0;
}