图论1：哥尼斯堡七桥问题的证明

 

图论1：哥尼斯堡七桥问题的证明

结论的证明

很久很久以前，有个大名鼎鼎的地方，叫哥你是宝哥尼斯堡。。

哥尼斯堡有一条河，河里有两座小岛，两座小岛和周边的陆地总共有七座桥连接起来。这里风景优美，空气新鲜，以至于很多市民都喜欢来这边旅游观光。

Figure 1. 风景优美，空气新鲜的哥尼斯堡七桥

 

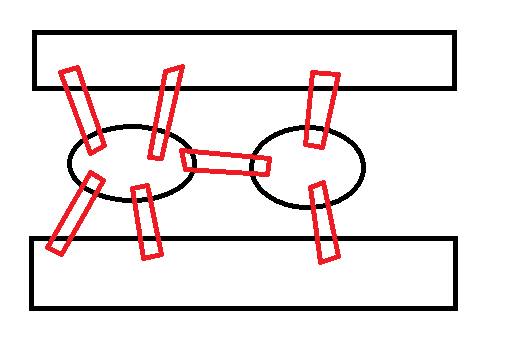
【NOTE】

红色方框表示桥，黑色方框表示陆地。

慢慢的，乐于游玩的市民们就想到一个问题： 有没有一种办法，可以从任意一个地方出发，然后恰巧每个桥只经过一次，观赏完所有风景之后又回到起点呢？

市民们使用了各种方式：

 

Figure 2. 这样的

 

Figure 3. 这样的

 

Figure 4. 这样的

……

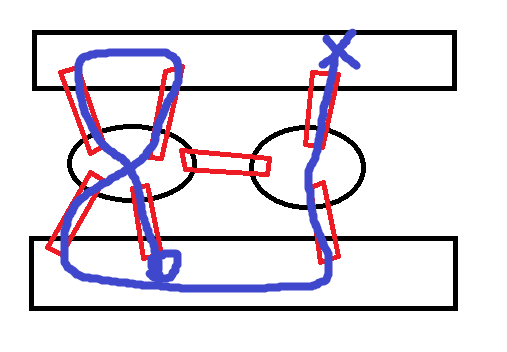
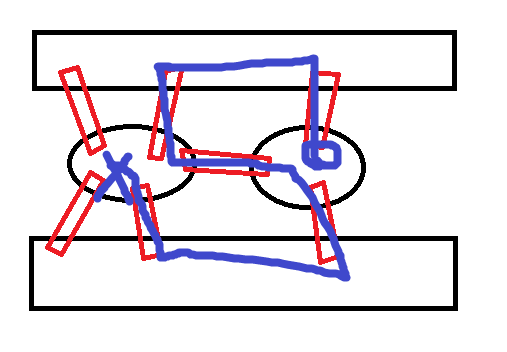
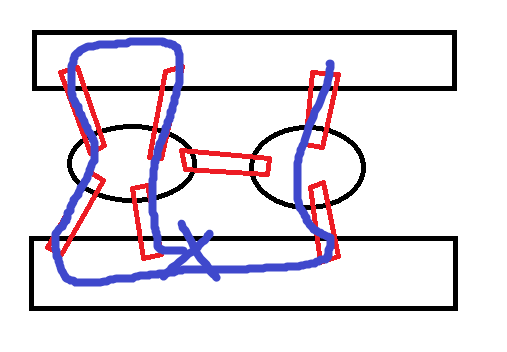
但不管怎么样都做不到。。

 

 

于是有人把这个问题写了封信，寄给了当时大名鼎鼎的数学家欧拉，

致敬欧拉大师

 

欧拉花了一年时间，最终证明了这个问题是无解的！

 

 

那么怎么去证明这个问题无解嘞？

 

欧拉大师先把地图模型简化成这样的二维模型：

 

Figure 5. 风景优美，空气新鲜的哥尼斯堡七桥

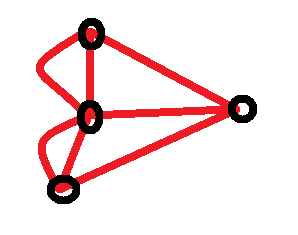
【NOTE】

红色方框表示桥，黑色方框表示陆地。这地方漂亮极了。

 

于是简化成了四个点、七条边，如何证明一个图形，从任意一点出发，每条边仅经过一次，最终又回到起点呢？

这个问题还是有点复杂，我们再对问题做一次简化，把七条边简化成一条，把四个点简化成一个点，那么得到如下模型：

 

Figure 6. 简化版的陆地和桥

 

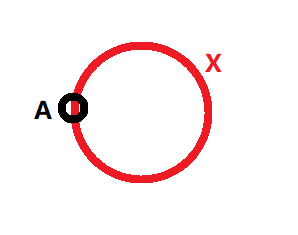
这……这不就是一个圆嘛！！

 

我们给图里的圆下一个定义：

从一个点出发，经过若干条边和点之后，最终能够回到原点，整个经过的路径我们称之为圆。

 

所以，七桥问题其实等同于画圆问题！

不管有几个顶点，也不管有几条边，从一点出发最终回到该点，本质上就是画圆。

所以对于上述证明问题，本质上就是求解能否在图形上构造出一个圆。

 

对“简化版的陆地和桥”做一层抽象，其实图中只具备两个元素：

A岛：连接着X桥。

X桥：首尾两端都连接着A岛。

 

欧拉大师略加思索，得出一个结论，在最简单的情况下，从能够从A点画圆的充要条件为：A点必须具备一个出口，同时也必须具备一个入口。

然后我们可以引入一个概念，将点A的入口/出口的数量统称为点A的 度 。

 

让我们再做一次扩展，为A岛再建造一座桥：

 

Figure 7. 稍微复杂一点的陆地和桥

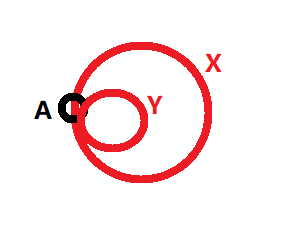
路线不管是 A → X → A → Y → A 还是 A → Y → A → X → A，依然可以回到原点。

A岛：连接着X桥。

X桥：首尾两端都连接着A岛。

Y桥：首尾两端都连接着A岛。

此时，A岛具备了两个入口和两个出口（4个度）。

 

之后，我们还可以再建造第三座桥、第四座桥，但不管建造几座桥，A点的出口数量必须等于入口的数量（即A点的 度 必须是偶数），否则就无法画圆： 

 

Figure 8. 只有出口或只有入口的A岛

 

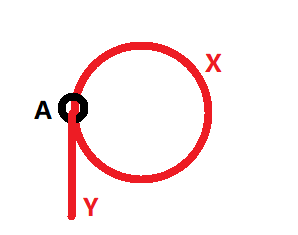
然后我们再回过头来看我们的“七桥”。

 

Figure 9. 风景优美、空气新鲜的七桥

 

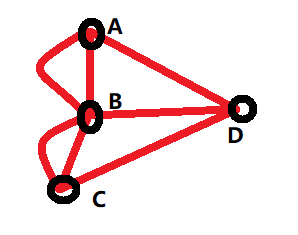
其中，A、C、D点的度为3，B点的度为5，都是奇数，这就意味着它没有能够画圆的起点/终点。

所以欧拉大师得到结论：该问题无解！

 

 

欧拉的回路

但欧拉也不愧是数学界的大师，因为他并没有止步于证明七桥问题无解。

他往前又做了更深一层的思考：

七桥问题既然是无解的，那么什么情况下才能使问题有解呢？

要从一个点出发，最终又能回到同一点的必要条件，是起点的度必须大于0且为偶数。

而其它的点因为不是起点也不是终点，所以不能停留，一旦进入则必须走出去，所以它们的度也必须大于0且为偶数。

最后，为了经过所有的顶点和边，还必须保证所有的顶点的边是联通的，否则无法在图中只构造出一个圆。

简而言之就是两个条件： 1. 所有顶点的度都必须是偶数。 2. 所有的顶点和边都能够联通。

我们随便画一个图验证一下：

Figure 1. 五角星

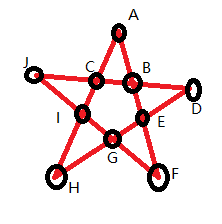
所有点的度都是偶数，所以任意一点出发都能回到原点。

C → A → B → D → E → F → G → H → I → J → C → B → E → G → I → C

还有很多其它路径，咱们就不一一解释啦。

其实这也很符合一个画圆的规律：在已知的圆上任取一点，都可以沿着路径画出同样一个完整的圆。

后来，人们把符合上述条件的路径，称为 欧拉回路。

 

 

欧拉的路径

欧拉大师画完圆了之后，感觉还不得劲，这问题太简单了。

能不能不回到起点，然后又能一条路走完全场呢？

依然按照之前的思路：

如果不想回到起点，那么起点必须具备的条件为：只能有奇数个度。

终点因为至少需要一次进入了之后再也不会出去，也必须具备一个条件：只能有奇数个度。

而其它的点因为不是起点也不是终点，所以不能停留，一旦进入则必须走出去，所以它们的度也必须大于0且为偶数。

简而言之也是两个条件： 1. 只能有两个顶点的读为奇数，其他顶点的度必须大于0且为偶数。 2. 所有的顶点和边都能够联通。

我们再随便画个图验证一下：

Figure 2. 加了一笔的五角星

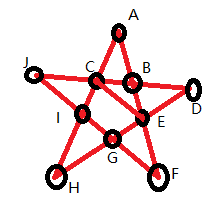
其中只有I和B两个点的度为奇数，因此只能从这两个点出发：

E → C → …… → C（参考没加一笔的五角星的路径）

就这么简单。

后来，人们把符合上述条件的路径，称之为欧拉路径。

这，就是哥尼斯堡七桥的故事。

欧拉大师也因此成为了最早的图论的研究者之一。

 

 ========================================================================================================

本节涉及到的概念：

图：

文字表述：包含若干个顶点和若干条边的集合。

数学表述：图G是一个有序二元组(V,E)，其中V称为顶集(Vertices Set)，E称为边集(Edges set)，E与V不相交。它们亦可写成V(G)和E(G)。

 

自环（Loop）：若一条边的两个顶点为同一顶点，则此边称作自环。

 

度：一个顶点的度是指与该顶点相关联的边的条数，顶点v的度记作d(v)。自环边由于既是入度又是出度，因此度为2。

入度：指顶点与其关联的各边之中，以其为终点的边数。

出度：指顶点与其关联的各边之中，以其为起点的边数。

 

欢迎读者们提出宝贵的意见或建议，作者会持续改进。