[每日一题]:D. Make The Fence Great Again

题目:

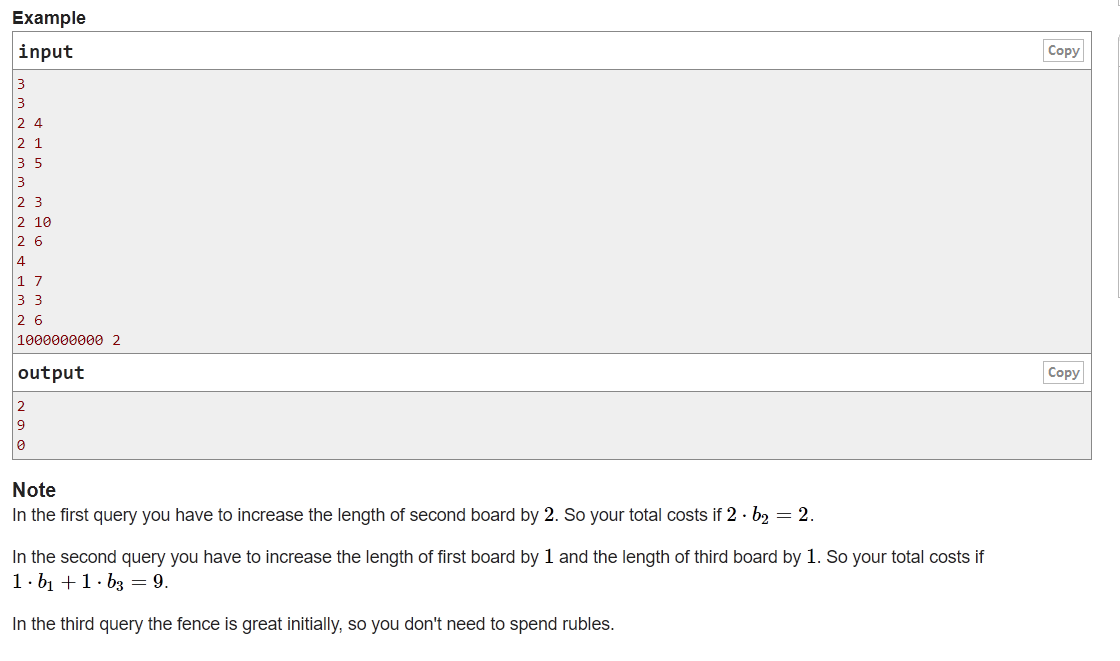
题目大意:

  给一个序列,要求两个相邻的 数之间不能相等(a[i - 1] != a[i])，每次 a[i] 增加 1 则
  相对应的需要花费 b[i] 的代价,问整个序列都要满足 a[i] != a[i - 1] 这样的条件需要
  花费的最小代价。

分析:

  首先要明白一点：两个相邻的数之间有三种关系：a = b,a < b,a > b;
  三种关系表明了我们应该增加哪个数,相应的会付出多大的代价。
  第二点:每个 a[i] 最多增加 2 就会满足相邻的两个数不相等。
  看这样一个序列: idx value weight
                  1    1     20
                  2    1      3
                  3    2      8
  从中发现,要使得前两个不等,必然第二个增加 1
  但增加 1 后发现 又跟第 3 个 相等了并且第 2
  个增加 1 的代价是最少的,所以总的来说 第二个
  总共增加两次。
  
  dp[i][j]：第 i 个增加 j 的最小代价(包括前 i - 1 个）

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

#define INF 0x3f3f3f3f

using namespace std;

typedef long long LL;

const int maxn = 3e5 + 10;
 
// dp[i][j] : 前 i 个满足相邻两个数不相等的最小代价 ,j 是每个 a[i] 的增量 
LL dp[maxn][3],a[maxn],b[maxn]; 
 
int q,n;

int main(void) {
	scanf("%d",&q);
	while(q --) {
		scanf("%d",&n);
		// 初始化 
		for(int i = 0; i <= n; i ++) {
			dp[i][0] = dp[i][1]  = dp[i][2] = 1e18;
		}
		for(int i = 1; i <= n; i ++) {
			scanf("%lld%lld",&a[i],&b[i]);
		}
		// 第一个本身不用和其他的进行比较 
		dp[1][0] = 0,dp[1][1] = b[1],dp[1][2] = 2 * b[1];
		for(int i = 2; i <= n; i ++) {
			for(int j = 0; j < 3; j ++) {                    // 第 i - 1 个 
				for(int k = 0; k < 3; k ++) {				 // 第 i 个 
					if(a[i] + k != a[i - 1] + j) {		     // 使相邻的两个数不相等的最小代价 
						dp[i][k] = min(dp[i][k],dp[i - 1][j] + k * b[i]);
					}
				}
			}
		}
		printf("%lld\n",min(dp[n][0],min(dp[n][1],dp[n][2])));
	}
	return 0;	
}