[每日一题]:Codeforces Round #640 (Div. 4) E. Special Elements

题目:

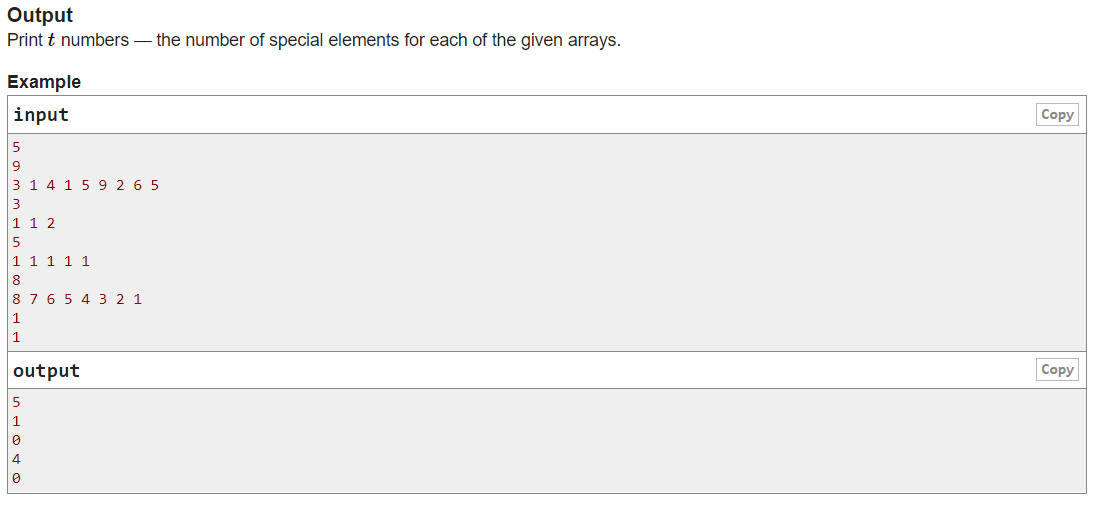
题目大意:

  给一个序列,然后问序列中的某个数是否可以通过序列中的一段连续的数相加得到（一个数是不行的）。
  满足这样的条件的数有几个？

侃侃:

  最初想法:
  因为是连续,而序列中一定存在一个最大值,如果说一段连续的值相加之和都超过最大值了，必然是不满足条件的,
  这时候就可以直接break了。
  最初想的是重新弄一个数组然后排序进行二分查找,每次得到一个新的 sum 值的时候就二分一下,虽然二分的时间
  复杂度是 log(N) 的,但是也禁不起这么多的小区间进行二分啊。
  然后就超时了。
  正解:
  深深体会一下连续的意味，又说要求和,想一下前缀和,不就是可以得到一个区间的和吗？
  题目中还说序列中所有的数都不会超过 n，用一个双循环来遍历可能的区间(当然时间复杂度必然不是 n^2 的,按照我们最初的想法,
  到一定的范围的时候 sum 必然是会 > n 的,这时候直接 break 即可)
  然后我们用一个标记数组来记录每个合法区间的 和,最后跟原数组相比,统计一下即可。

Code:

TLE代码：

#include <map>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

#define INF 0x3f3f3f3f

using namespace std;

const int maxn = 8005;

int a[maxn],b[maxn];

int t,n,res; 

map<int,int>maps;

int Check(int x) {
	int l = 1,r = n + 1;
	while(l < r) {
		int mid = l + r >> 1;
		if(b[mid] >= x) r = mid;
		else l = mid + 1;
	} 
	if(b[r] == x) {
		res += maps[b[r]];
		maps[b[r]] = 0;	
	}
	return b[r];
}

int main(void) {
	scanf("%d",&t);
	while(t --) {
		res = 0;
		scanf("%d",&n);
		for(int i = 1; i <= n; i ++) {
			scanf("%d",&a[i]);
			b[i] = a[i];
			maps[b[i]] ++;
		}
		sort(b + 1, b + 1 + n);
		b[n + 1] = INF;
		int sum = 0;
		for(int i = 1; i < n; i ++) {
			sum = a[i];
			for(int j = i + 1; j <= n; j ++) {
				sum += a[j];
				if(Check(sum) == INF) {
					break;
				}
			}
			
		}
		printf("%d\n",res);
		maps.clear();
	}
	return 0;
}

AC代码：

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 8005;

int a[maxn],vis[maxn];
int preSum[maxn];

int t,n;

int main(void) {
	scanf("%d",&t);
	while(t --) {
		memset(vis,0,sizeof(vis));
		scanf("%d",&n);
		for(int i = 1; i <= n; i ++) {
			scanf("%d",&a[i]);和 
			// 前缀 
			preSum[i] = preSum[i - 1] + a[i];
		}
		for(int i = 1; i <= n; i ++) {
			for(int j = i + 1; j <= n; j ++) {
				int value = preSum[j] - preSum[i - 1];
				// 如果区间值 > n ,说明后面的更不可能了 
				if(value > n + 1) break;
				// 将合法区间的 和 进行 标记一下 
				vis[value] = 1;
			}
		}
		int ans = 0;
		for(int i = 1; i <= n; i ++) {
			
			if(vis[a[i]]) ans ++;
		}
		printf("%d\n",ans);
	}
	return 0;
}