[每日一题]:B. Phoenix and Beauty

题目:

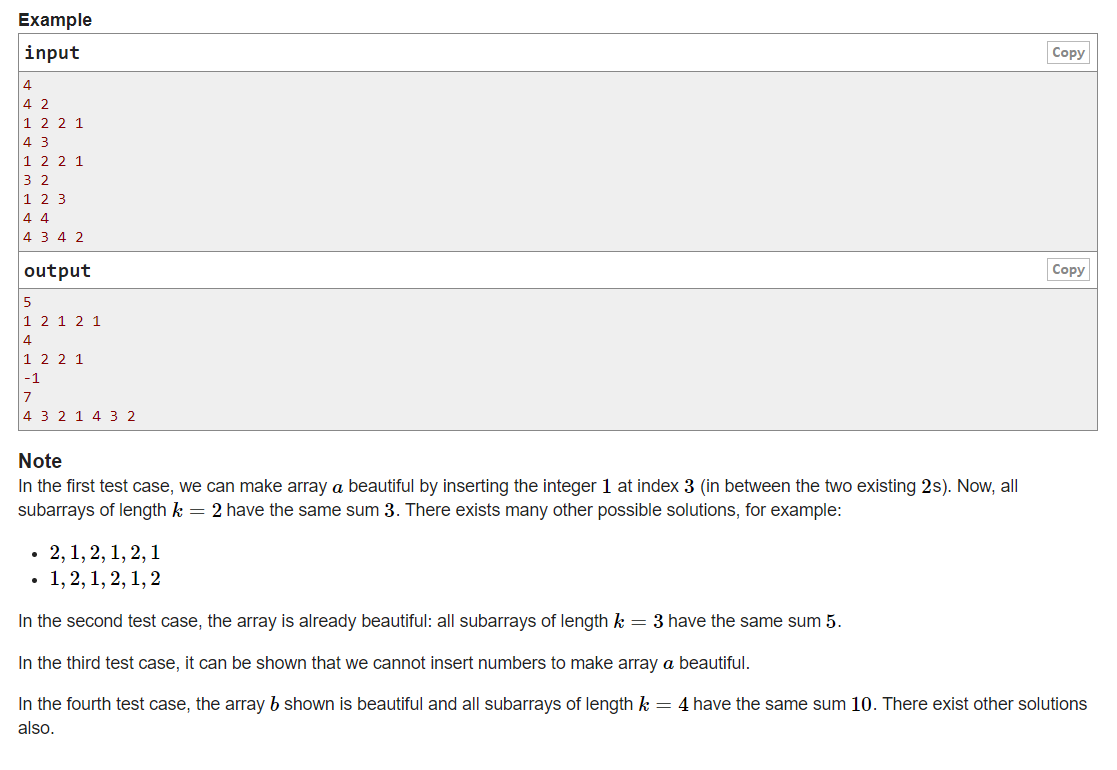
题目大意:

给一个数组 A ,有一个 K ,代表子序列的区间大小是 k ,可以向数组 A 中插入元素组成一个新的数组,问
是否可以使得新数组满足 每个 区间大小为 k 的子序列的元素和相同。

考察点:

构造、贪心、思维

侃侃:

构造题是真的不好想啊,这里需要想清楚几个点:
1、如何使得我们构造的数组成为一个常态（即满足所有的测试）
2、构造的新数组中 不同的元素个数 == k
   (关于这点刚开始一直没想清楚,之后看到大佬写的才慢慢理解)
  如果 不同的元素个数 > k ,我们是无法构造出一个符合条件的数组的。
  会出现一个循环节: 1 3 5 (k = 2)
                   1 3 1 3 1 3 ...... 5
  cnt = 不同的元素个数:
  当 cnt < k 是我们可以向数组 A 中插入不同的数使得  cnt == k
  为什么要使得 cnt == k 呢？
  我们怎么能最快的构造出一个使得各个子序列的和相等？
  让 数组 A 中的每个数都对应 k 个数,我们最后的区间长度就是 n * k
  看一个例子:
  4 3 
  4 3 4 2
  构造: 1 2 3 4 1 2 3 4 1 2 3 4 1 2 3 4
  这样就可以使得我们的每个测试都是一个 常态了。
  是不是很神奇，哈哈，具体的证明咱也不太会。

Code:

#include <set>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 1e4 + 10;

int a[maxn],b[maxn];

bool vis[maxn];             // cnt < k 时查找不同的数 

int t,n,k;

int main(void) {
	scanf("%d",&t);
	while(t --) {
		// 初始化 
		set<int>sets;
		set<int>::iterator it;
		memset(vis,0,sizeof(vis));
		scanf("%d%d",&n,&k);
		for(int i = 1; i <= n; i ++) {
			scanf("%d",&a[i]);
			sets.insert(a[i]);
		}
		if(sets.size() > k) {
			puts("-1");
			continue;
		}

		printf("%d\n", n * k);
		int cnt = 0;
		// 遍历所有的不同的数 
		for(it = sets.begin(); it != sets.end(); it ++) {
			b[++ cnt] = *it;
			vis[*it] = true;
		}
		// cnt == k 时直接 n 个 k 即可 
		if(sets.size() == k) {
			for(int i = 1; i <= n; i ++) {
				for(int j = 1; j <= k; j ++) {
					printf("%d ",b[j]);
				}
			}
		} else {
			// cnt < k 时补足 k 个 
			int num = sets.size();
			for(int i = 1; i <= n; i ++) {
				if(!vis[i]) b[++ cnt] = i,num ++;
				if(num == k) break;
			}
			for(int i = 1; i <= n; i ++) {
				for(int j = 1; j <= k; j ++) {
					printf("%d ",b[j]);
				}
			}
		}
		puts("");
	}
	return 0;
}

后记:

构造的题不太好想,需要找到问题的一些性质,从而构造出一个
符合所有测试样例的 Answer.
加油！