[每日一题]: CodeForces 685B Kay and Snowflake

题目:

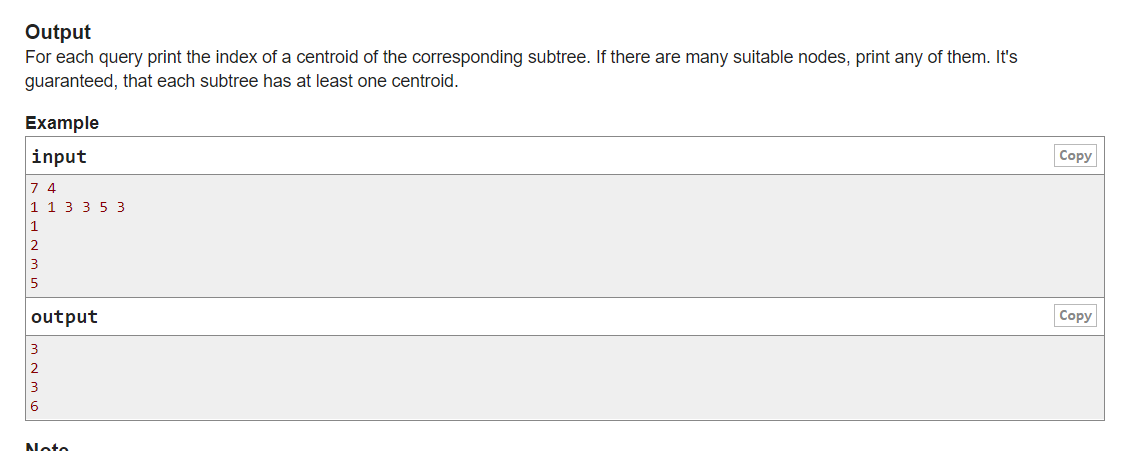
题目大意:

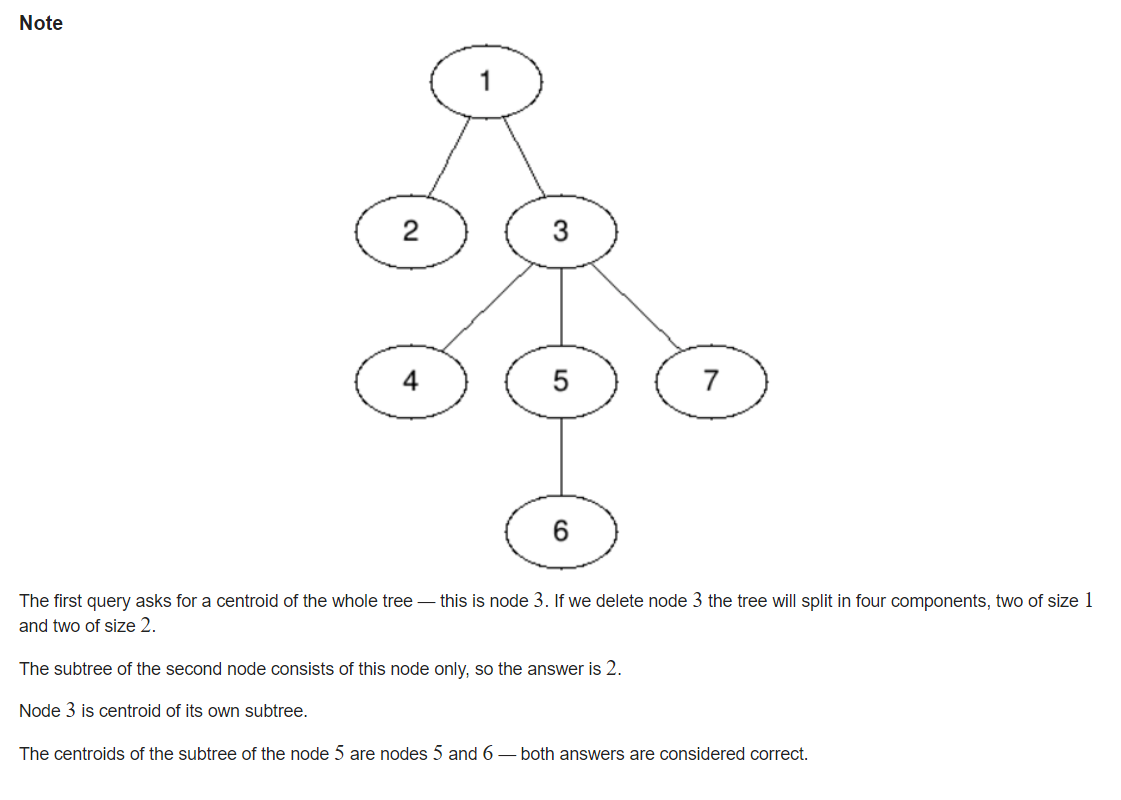
给一棵树，接着给一个节点，作为一棵子树的根节点，问以这个节点为根的树的重心是多少？

树的重心不了解的戳这里:

https://www.cnblogs.com/prjruckyone/p/12793007.html

侃侃:

这道题问的比较清晰易懂,但是实现起来较有难度,主要是利用树形 DP 的思想。
由底向上得到信息,如果这道题查询范围较小的话，我们可以直接利用树的重心
的板子进行求解即可,但是这道题查询的数据范围较大,查询的话时间肯定会崩的。
本菜鸡就亲身尝试了，哈哈。
这里就需要用到 树的重心中的几个性质进行优化。

本题用到的几个性质:

1、把两棵树通过一条边相连，新的树的重心在原来两棵树重心的连线上。
(一个节点也是一棵树，所以我们递归到最深处，两个节点就是两棵树
然后就可以用这个性质了，一个节点的重心即它本身)
2、以这个点为根，那么所有的子树（不算整个树自身）的大小都不超过
整个树大小的一半。
我们就可以根据这个性质进行自底向上更新。

Code:

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

#define INF 0x3f3f3f3f

using namespace std;

const int maxn = 3e5 + 10;

int h[maxn],ve[maxn],Ne[maxn],e[maxn];
int vis[maxn],Size[maxn],fa[maxn];

int n,q;
int tot,u,v;
int center[maxn],min_port,pos;

void add(int u,int v) {
	ve[++ tot] = v;
	Ne[tot] = h[u];
	h[u] = tot;
	return ;
}

void DFS(int x,int f) {
	Size[x] = 1;
	// 到叶节点时一定是它自己 
	if(h[x] == Ne[h[x]]) {
		center[x] = x;
		return ;
	} 
	
	int max_port = 0,pos = 0;
	// 寻找 以 x 为根的最大子树的 根节点 
	for(int i = h[x]; i; i = Ne[i]) {
		int y = ve[i];
		if(y == f) continue;
		DFS(y,x);
		Size[x] += Size[y];
		if(Size[y] > max_port) {
			pos = y;
			max_port = Size[y];
		}
	}
	center[x] = center[pos];
	// 以重心为根,那么所有的子树的大小都不超过整个树大小的一半 
	while(Size[center[x]] * 2 <= Size[x]) {
		center[x] = fa[center[x]];	
	}
	return ;
}

int main(void) {
	scanf("%d%d",&n,&q);
	for(int i = 2; i <= n; i ++) {
		scanf("%d",&v);
		fa[i] = v;
		add(v,i);
//		add(i,v);
	}
	int st = 0;
	DFS(1,-1);
	while(q --) {
		scanf("%d",&st);
		printf("%d\n",center[st]);
	}
	return 0;
}