分块大法 -- 优雅的暴力

饭前点心:

分块，就是剁吧剁吧将一整块分成一小块一小块的,再连到一起。
回顾一下之前学习的数据结构，树状数组是基于 二进制划分和倍增 思想，
线段树是基于 分治 思想,它们之所以能高效的在一个序列上执行指令并且
统计信息，就是因为他们把序列中的元素聚合成大大小小的段，花费额外的
代价对这些 段 进行维护，从而使得每个区间的信息可以快速由几个已有的
段 结合而成。
分块的基本思想是通过适当的划分，预处理一部分的信息并保存下来，用空间
换取时间，从而达到平衡。
相比来说，分块更易于实现，代码来说也比较容易理解。

拿个板子侃侃:

空侃比较没有依据,我们拿一道模板题来侃侃这个 优雅的暴力。

关于模板:

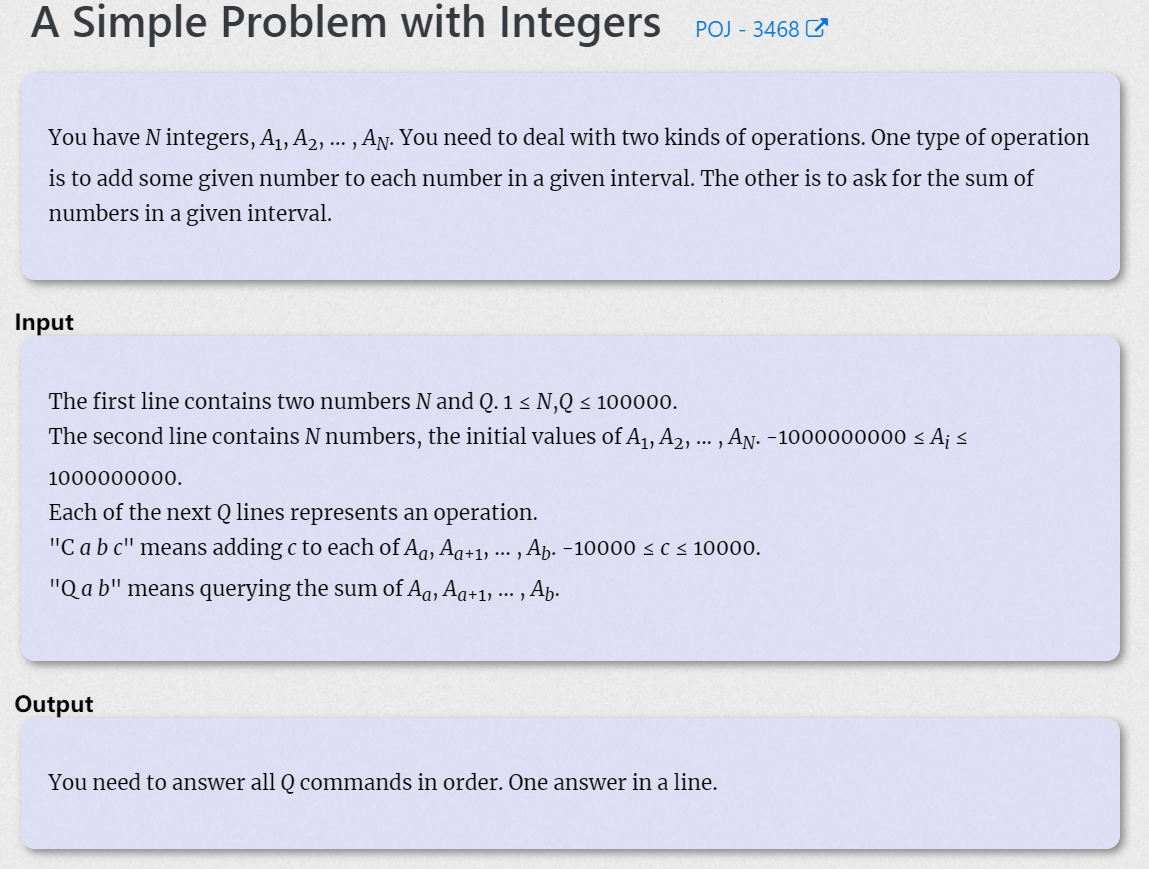
题目说，给一个数列,然后有两种操作：
1、把数列中第 l ~ r 个数都加 d。
2、询问数列中第 L ~ r 个数的和。

看到这两个操作，你可能会想，这不是区间查询和区间修改吗？
直接线段树不就 Ok 了,线段树当然可以，但是在这里用分块
的话应该做点什么呢？
Look Down

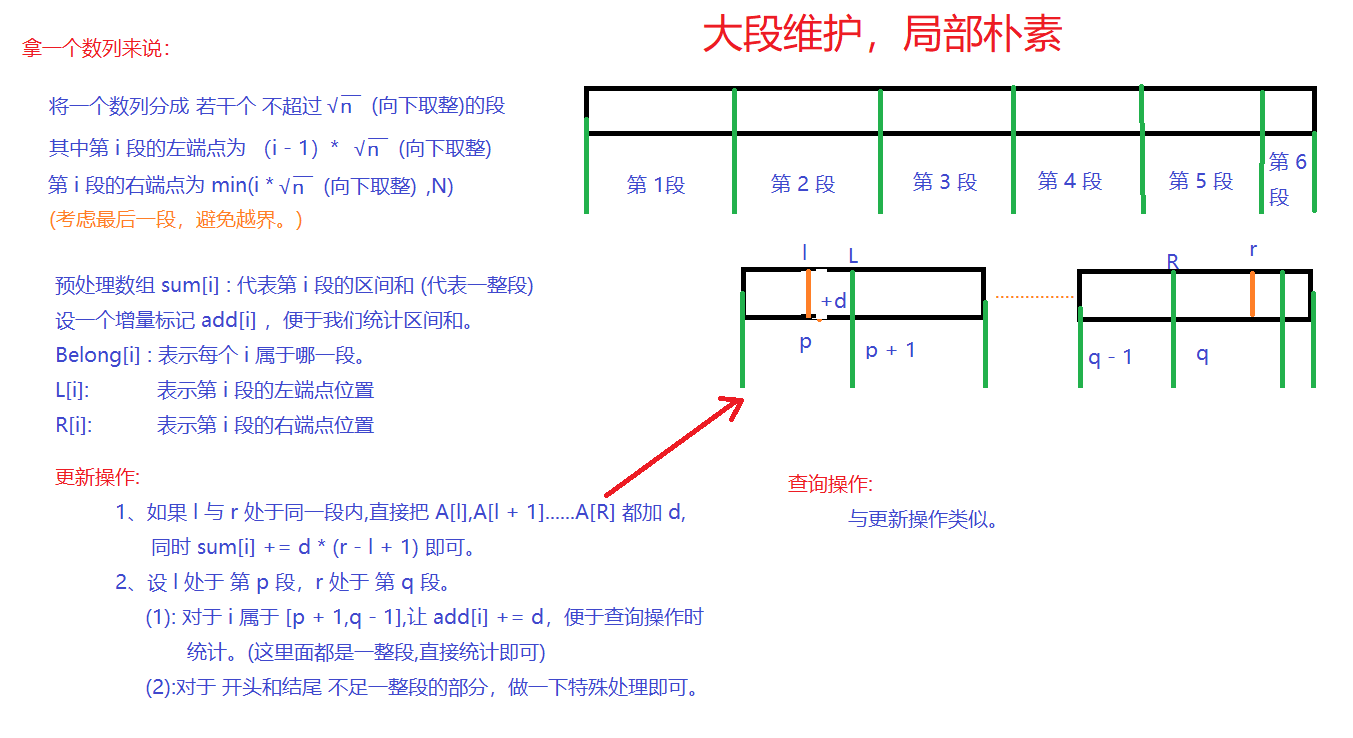
分什么，怎么分？

带着这些疑问，听我向你娓娓道来:

Code：

#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

using namespace std;

const int maxn = 1e5 + 10;

typedef long long LL;

/*
	belong[]: i 属于那一段
	L[i]    : 第 i 段的左边位置
	R[i]	: 第 i 段的右边位置 
	block	: 每段有多大 
	num		: 有多少段 
*/


LL sum[maxn],add[maxn],a[maxn];
int belong[maxn],L[maxn],R[maxn];

LL num;
LL block;

LL n,q,l,r,x;

string op;

// 初始化 
void build() {
	block = sqrt(n);
	num = n / block;
	// 奇数就多一段 
	if(n % block) num ++;
	// 每段的起点和终点 
	for(int i = 1; i <= num; i ++) {
		L[i] = (i - 1) * block + 1;
		R[i] = i * block;
	}
	// 取最小,避免越界 
	R[num] = n;
	// i 属于哪一段 
	for(int i = 1; i <= n; i ++) {
		belong[i] = (i - 1) / block + 1;
	}
	// 初始化,求每一段的和 
	for(int i = 1; i <= num; i ++) {
		for(int j = L[i]; j <= R[i]; j ++) {
			sum[i] += a[j];
		}
	}
	return ;
}

// 更新 
void update(LL l,LL r,LL x) {
	LL p = belong[l],q = belong[r];
	// 在同一块内直接操作 
	if(p == q) {
		for(int i = l; i <= r; i ++) {
			a[i] += x;
		}
		// 更新 sum 
		sum[p] += x * (r - l + 1);
	} else {
		// 中间的整段 
		for(int i = p + 1; i <= q - 1; i ++) add[i] += x;
		// 左侧多余的 
		for(int i = l; i <= R[p]; i ++) a[i] += x;
		sum[p] += x * (R[p] - l + 1);
		// 右侧多余的 
		for(int i = L[q]; i <= r; i ++) a[i] += x;
		sum[q] += x * (r - L[q] + 1);
	}
	return ;
}

// 查询 
LL ask(LL l,LL r) {
	LL ans = 0;
	LL p = belong[l],q = belong[r];
	if(p == q) {
		for(int i = l; i <= r; i ++) {
			ans += a[i];
		}
		ans += add[p] * (r - l + 1);
	} else {
		// 先处理整段,不仅要加上原有的,还有增加的 
		for(int i = p + 1; i <= q - 1; i ++) {
			ans += sum[i] + add[i] * (R[i] - L[i] + 1); 
		}
		for(int i = l; i <= R[p]; i ++) ans += a[i];
		ans += add[p] * (R[p] - l + 1);
		for(int i = L[q]; i <= r; i ++) ans += a[i];
		ans += add[q] * (r - L[q] + 1); 
	}

	return ans ;
}

int main(void) {
	scanf("%lld%lld",&n,&q);
	for(int i = 1; i <= n; i ++) {
		scanf("%lld",&a[i]);
	}
	build();
	while(q --) {
		cin >> op;
		if(op == "Q") {
			scanf("%lld%lld",&l,&r);
			printf("%lld\n",ask(l,r));
		} else {
			scanf("%lld%lld%lld",&l,&r,&x);
			update(l,r,x);
		}
	}
	return 0;
}

后记：

分块--优雅的暴力,名不虚传,但是效率来说相对于线段树和树状数组来说是比较
低的。