[每日一题]:Codeforces Round #635 (Div. 2) D. Xenia and Colorful Gems

题目:

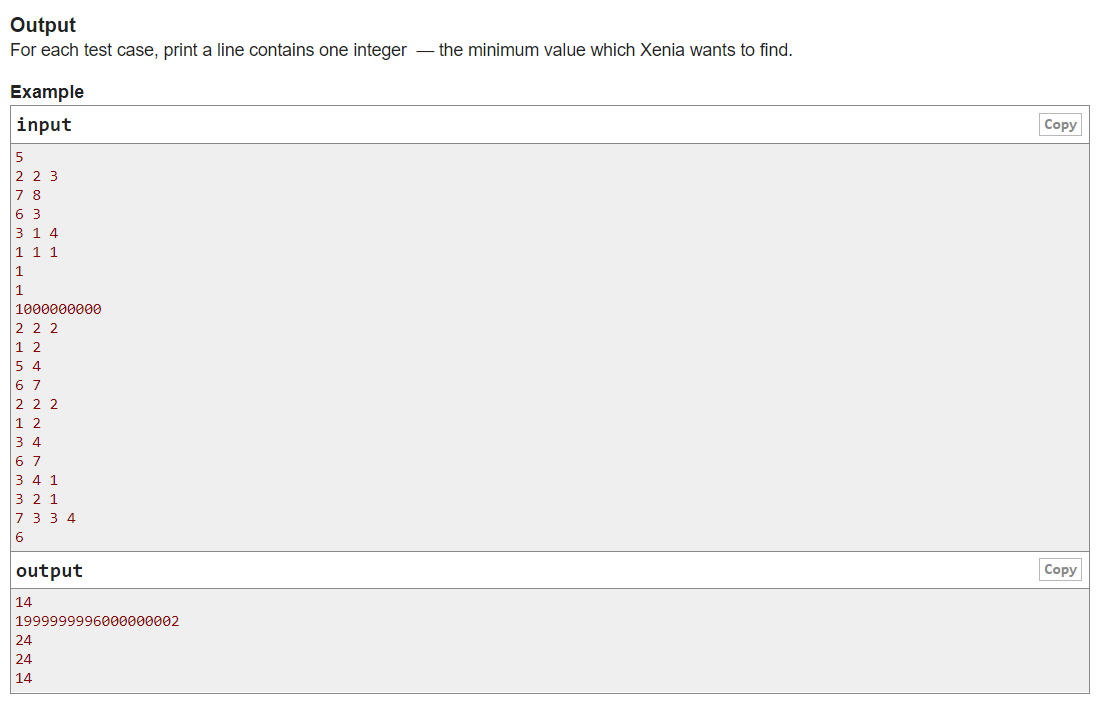
题目大意:

有三个数组,从每个数组中选一个数使得 (x - y) ^ 2 + (y - z ) ^ 2 + (z - x) ^ 2 的值最小。    

考察点:

思维推理、二分、longlong 的最大值范围

侃侃:

题意还是比较好懂得,纯暴力去做的话样例过去都有点悬,所以要怎么优化呢？
一般这类题都是观察这个式子,从式子中寻找相关联的东西,例如某个值对另
一个值的影响,以及单调性等性质。

图解:

Code:

#include <vector>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

#define INF 0x3f3f3f3f3f3f3f3f

using namespace std;

const int maxn = 1e5 + 10;

typedef long long LL; 

int t;

LL res = 0;

void solve(vector<LL>a,vector<LL>b,vector<LL>c) {
	vector<LL>::iterator y,z;
	for(int i = 0; i < a.size(); i ++) {
		y = lower_bound(b.begin(),b.end(),a[i]);
		z = upper_bound(c.begin(),c.end(),a[i]);
		// 没有比当前 x 大的或者 没有比 x 小的,说明当前枚举的方法不可行 
		if(y == b.end() || z == c.begin()) continue;
		// 找比 x 小的,使得 x 成为中间的数 
		z --;
		res = min(res,(a[i] - *y) * (a[i] - *y) + (*y - *z) * (*y - *z) + (*z - a[i]) * (*z - a[i]));
	}
}

int main(void) {
	scanf("%d",&t);
	while(t -- ) {
		LL na,nb,nc;
		scanf("%lld%lld%lld",&na,&nb,&nc);
		vector<LL>r(na),g(nb),b(nc);
		for(int i = 0; i < na; i ++) {
			scanf("%lld",&r[i]);
		}
		for(int j = 0; j < nb; j ++) {
			scanf("%lld",&g[j]);
		}
		for(int k = 0; k < nc; k ++) {
			scanf("%lld",&b[k]);
		}
		
		sort(r.begin(),r.end());
		sort(g.begin(),g.end());
		sort(b.begin(),b.end());
		// longlong 能表示的最大值 是 9e18 
		res = INF;
		solve(r,g,b),solve(r,b,g),solve(g,r,b);
		solve(g,b,r),solve(b,r,g),solve(b,g,r);
		
		printf("%lld\n",res);
	}
	return 0;
} 

后记:

对二分查找函数有了更加深刻的理解,既然我们能找到第一个 >= x 的值,自然也能找到第一个 < x 
的值,用 vector 充当数组还是挺方便的。