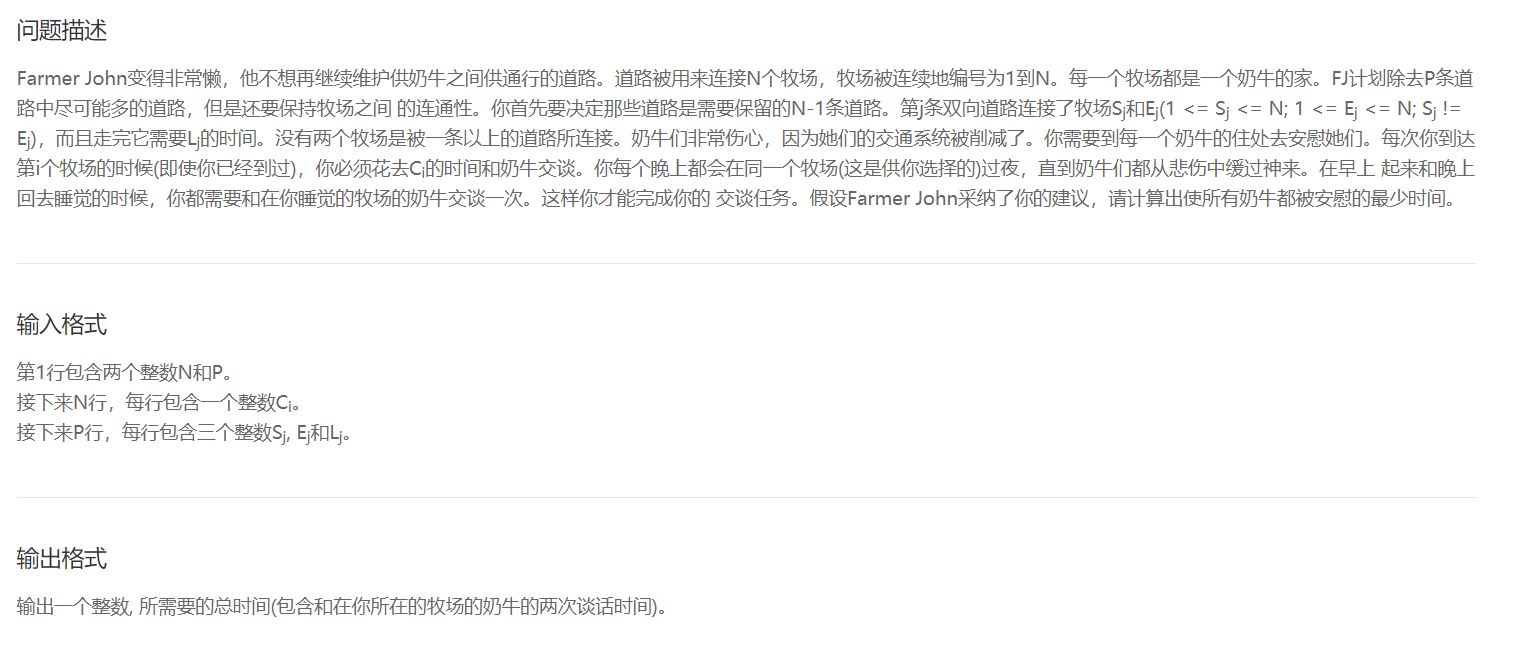
[每日一题]:[Usaco2008Nov]安慰奶牛

题目:

样例:

蓝桥杯上的样例是错误的,之后从网上查了一下,下面附上正确的样例:

Sample Input
5 7
10
10
20
6
30
1 2 5
2 3 5
2 4 12
3 4 17
2 5 15
3 5 6
4 5 12

Sample Output
176

析题得侃:

这道题真的是有点难懂呀,对语文不好的我来说简直太难了。
不得已,只能参考网上大佬的解释了。
大致就是说:
一个牛从一个起点出发,遍历整棵树之后再回到起点,直到离开整棵树(这句是自己猜的)
然后求一下最小的花费(每个节点上有权值,每条路径上也有花费的时间,满足最优的一种方案)

考察点: 最小生成树

侃侃题解:

我们最终求得是走完所有点后又回到起点的一条路线,假设我们从 A -- > B,最后再从 B -- > A
那我们所花费的代价就是 A + W(A,B) + B + B + W(B,A) + A
那么可以得知树上的每一条边应该都是这样的。
所以我们可以按照这个新的权值进行建一棵最小生成树即可。

另外,最后还要 + 最小的节点权值,我想是因为我们最后离开所有的奶牛时还需要安慰一下起点处的奶牛
(如有更合适的解释,希望大佬一定告诉我,在此万分感谢)

Code:

#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

#define INF 0x3f3f3f3f

using namespace std;

const int maxn = 2e5 + 10;

typedef long long LL;

struct node {
	LL u,v,w;
}cow[maxn];

bool cmp(node a,node b) {
	return a.w < b.w;
}

LL value[maxn],fa[maxn];

int n,p;

LL get(int x) {
	return x == fa[x] ? x : fa[x] = get(fa[x]);
}

void Union(int x,int y) {
	int xx = get(x);
	int yy = get(y);
	if(xx == yy) return ;
	fa[yy] = xx;
	return ; 
}

int main(void) {
	LL minValue = INF;
	scanf("%d%d",&n,&p);
	for(int i = 1; i <= n; i ++) {
		fa[i] = i;
	}
	// 寻找最小的节点作为出发地 
	for(int i = 1; i <= n; i ++) {
		scanf("%lld",&value[i]);
		minValue = min(value[i],minValue);
	}
	int u,v,w;
	// 根据节点与边之间的关系找到新的权值,更适合建立生成树 
	for(int i = 1; i <= p; i ++) {
		scanf("%d%d%d",&u,&v,&w);
		cow[i].w = value[u] + value[v] + 2 * w;
		cow[i].u = u,cow[i].v = v;
	}
	sort(cow + 1,cow + 1 + p,cmp);
	LL sum = 0;
	
	for(int i = 1; i <= p; i ++) {
		int x = cow[i].u,y = cow[i].v,w = cow[i].w;
		if(get(x) == get(y)) continue;
		Union(x,y);
		sum += cow[i].w; 
	}
	
	printf("%lld\n",sum + minValue);
	return 0;
} 

后记:

题都没读懂,样例也没推出来(虽然说是错的),hh,有点丢人，还是自己太菜了。
收获的地方感觉就是更加了解怎样去生成一个最小树,怎么样更加合适,只有找
到合适的权值,我们所求得的最小生成树才更有意义。
也算复习了一下最小生成树。
加油！