分治 -- 平面最近点对

平面最近点对 :

分析各种情况 :

首先将所有点对按照 x 作为第一关键字进行排序,然后从中间进行劈开,进行递归分治
最后答案就是 res = min(l -- mid,mid + 1 -- r);

从上图可以得知 : 要求在这个平面内所有点中的最近点对,会有三种情况:
                1、两个点都在左侧    
                2、两个点都在右侧
                3、一个点在左侧,一个点在右侧

分别向两侧递归进行分治 :

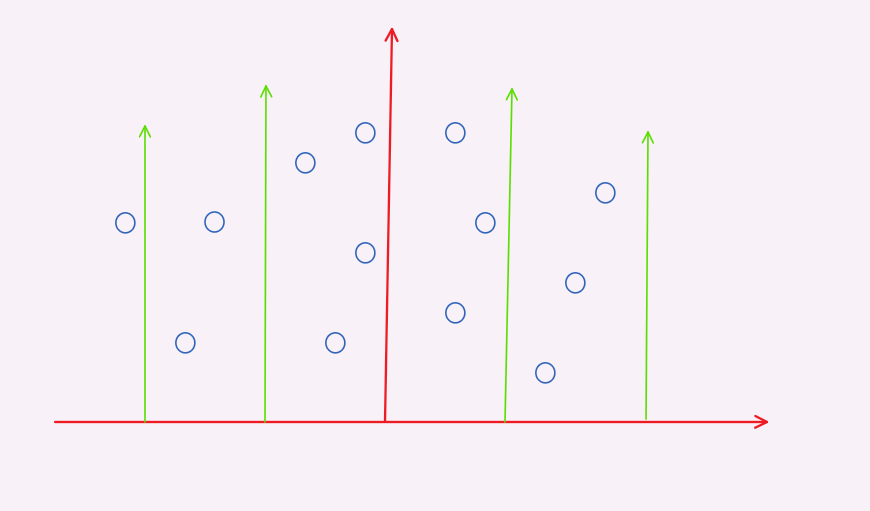
寻找最近点对 :

1、找到左侧的最近点对
2、找到右侧的最近点对
进行比较我们就会得到一个左侧和右侧之中的最近的一对
这时我们会得到一个最近点对的距离(是目前这个过程中最近的一对,假设 当前最近点对的距离是 res)
还差第三种情况 :  第三种情况是一个在左侧,一个在右侧,那么这些点一定是靠近 中间的 mid 的,
所以第三种情况的所有点一定是下面这种情况 (虚线的范围代表这些点可能会出现的范围): 

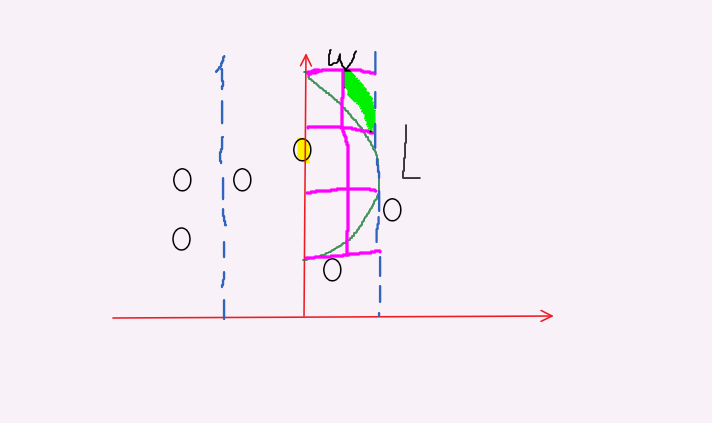
由于我们得到的最近点对的距离是 res,所以剩下的距离一定是要 < res 的,最多 == res，所以我们可以
求出在这个范围内与每个点可能会组成的点的数量,然后，按照纵坐标排序枚举这些(数量不会太多,不用担心会超时)
(如上图所示,最多只会有 6 个点 -- 每个方格内最多放一个点)

Code ：

#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

#define INF 0x3f3f3f3f

using namespace std;

const int SIZE = 1e5 + 10;
struct Point {
	double x,y;

	bool operator <( const Point &W)const {
		return x < W.x;
	}
} Points[SIZE],temp[SIZE];
int t,n;

int main(void) {
	double DFS(int l,int r);
	while(scanf("%d",&n) != EOF) {
		if(n == 0) break; 
		for(int i = 1; i <= n; i ++) {
			scanf("%lf%lf",&Points[i].x,&Points[i].y);
		}
                // 先将所有坐标按照横坐标进行排序--便于分治
		sort(Points + 1,Points + 1 + n);
		printf("%.2lf\n",DFS(1,n));
	}
	return 0;
}

// 求两个点之间的距离

double dist(Point a,Point b) {
	double dx = a.x - b.x;
	double dy = a.y - b.y;
	return sqrt(dx * dx + dy * dy);
}

double DFS(int l,int r) {
        // 将和自身的距离设为 无穷大
	if(l >= r) return INF;
        // 就两个点时直接返回两个点之间的距离即可
	if(l + 1 == r) return dist(Points[l],Points[r]);
	int mid = l + r >> 1;
        // 中间的 mid 部分,用于求第三种情况
	int mid_x = Points[mid].x;
        // 递归找到左右两端的最近点对
	double res = min(DFS(l,mid),DFS(mid + 1,r));
	{        // 归并排序(便于查找,省时间,不用每次都排序了)
		int k = 0,i = l,j = mid + 1;
		while(i <= mid && j <= r) {
			if(Points[i].y > Points[j].y) {
				temp[k ++] = Points[j ++];
			} else {
				temp[k ++] = Points[i ++];
			}
		}
		while(i <= mid) {
			temp[k ++] = Points[i ++];
		}
		while(j <= r) {
			temp[k ++] = Points[j ++];
		}
		for(int i = l; i <= r; i ++) {
			Points[i] = temp[i - l];
		}
	}
	int k = 0;
        // 寻找区域内的所有点
	for(int i = l; i <= r; i ++) {
		if(Points[i].x >= mid_x - res && Points[i].x <= mid_x + res) {
			temp[k ++] = Points[i];
		}
	}
        // 枚举区域内的所有点,寻找更近的点对
	for(int i = 0; i < k; i ++) {
		for(int j = i - 1; j >= 0 && temp[i].y - temp[j].y < res; j --) {
			res = min(res,dist(temp[i],temp[j]));
		}
	}
	return res;
}

例题:

1、Quoit Design

#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

#define INF 0x3f3f3f3f

using namespace std;

const int SIZE = 1e5 + 10;
struct Point {
	double x,y;

	bool operator <( const Point &W)const {
		return x < W.x;
	}
} Points[SIZE],temp[SIZE];
int t,n;

int main(void) {
	double DFS(int l,int r);
	while(scanf("%d",&n) != EOF) {
		if(n == 0) break; 
		for(int i = 1; i <= n; i ++) {
			scanf("%lf%lf",&Points[i].x,&Points[i].y);
		}
		sort(Points + 1,Points + 1 + n);
		printf("%.2lf\n",DFS(1,n) / 2);
	}
	return 0;
}

double dist(Point a,Point b) {
	double dx = a.x - b.x;
	double dy = a.y - b.y;
	return sqrt(dx * dx + dy * dy);
}

double DFS(int l,int r) {
	if(l >= r) return INF;
	if(l + 1 == r) return dist(Points[l],Points[r]);
	int mid = l + r >> 1;
	int mid_x = Points[mid].x;
	double res = min(DFS(l,mid),DFS(mid + 1,r));
	{
		int k = 0,i = l,j = mid + 1;
		while(i <= mid && j <= r) {
			if(Points[i].y > Points[j].y) {
				temp[k ++] = Points[j ++];
			} else {
				temp[k ++] = Points[i ++];
			}
		}
		while(i <= mid) {
			temp[k ++] = Points[i ++];
		}
		while(j <= r) {
			temp[k ++] = Points[j ++];
		}
		for(int i = l; i <= r; i ++) {
			Points[i] = temp[i - l];
		}
	}
	int k = 0;
	for(int i = l; i <= r; i ++) {
		if(Points[i].x >= mid_x - res && Points[i].x <= mid_x + res) {
			temp[k ++] = Points[i];
		}
	}
	for(int i = 0; i < k; i ++) {
		for(int j = i - 1; j >= 0 && temp[i].y - temp[j].y < res; j --) {
			res = min(res,dist(temp[i],temp[j]));
		}
	}
	return res;
}

2、袭击

#include <cmath>
#include <cstdio>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>

#define INF 0x3f3f3f3f

using namespace std;

const int maxn = 1e5 + 10;

struct Point{
	double x,y;
	int type;
	
	bool operator<(const Point &w) const {
		return x < w.x;
	}
	
}Points[maxn << 1],temp[maxn << 1];

int T,n;

int main(void) {
	double DFS(int l,int r);
	scanf("%d",&T);
	while(T --) {
		scanf("%d",&n);
		for(int i = 1; i <= n; i ++) {
			scanf("%lf%lf",&Points[i].x,&Points[i].y);
			Points[i].type = 0;
		}
		for(int i = n + 1; i <= n * 2; i ++) {
			scanf("%lf%lf",&Points[i].x,&Points[i].y);
			Points[i].type = 1;
		}
		sort(Points + 1,Points + (n << 1));
		printf("%.3lf\n",DFS(1,n << 1));
	}
	
	return 0;
} 

double dist(Point a,Point b) {
	if(a.type == b.type) return INF;
	double dx = (a.x - b.x) * (a.x - b.x);
	double dy = (a.y - b.y) * (a.y - b.y);
	return sqrt(dx + dy);
}


double DFS(int l,int r) {
	if(l >= r) return INF;
	if(l + 1 == r) return dist(Points[l],Points[r]);
	int mid = l + r >>  1;
	double mid_x = Points[mid].x;
	double res = min(DFS(l,mid),DFS(mid + 1,r));
	{
		int i = l,j = mid + 1,k = 0;
		while(i <= mid && j <= r) {
			if(Points[i].y > Points[j].y) {
				temp[k ++] = Points[j ++];
			} else {
				temp[k ++] = Points[i ++];
			}
		}
		while(i <= mid) {
			temp[k ++] = Points[i ++];
		}
		while(j <= r) {
			temp[k ++] = Points[j ++];
		}
		for(int i = l; i <= r; i ++) {
			Points[i] = temp[i - l];
		}
	}
	int k = 0;
	for(int i = l; i <= r; i ++) {
		if(Points[i].x >= mid_x - res && Points[i].x <= mid_x + res) {
			temp[k ++] = Points[i];
		}
	}
	for(int i = 0; i < k; i ++) {
		for(int j = i - 1; j >= 0 && temp[i].y - temp[j].y < res; j --) {
			res = min(res,dist(temp[i],temp[j]));
		}
	}
	return res;
}