数据结构与算法—C语言描述 树和二叉树的概念和定义

数据结构与算法——C语言描述 个人笔记

树和二叉树

---

前言

在生活中，线结构是最基本并且也是最常用的，但是有许多逻辑关系并不是简单的线性关系，在实际的场景中，往往存在一对多甚至是多对多的情况。

这时就需要非线性结构了，而树结构则是一类重要的非线性结构，树是以分支关系定义的层次结构，并且在现实生活中有广泛的应用。

比如说人类社会的家谱：

满 门 忠 烈

机构里的职级关系也可以用树表示：

还有许多抽象的东西也可以表示成一棵树，比如说操作系统中的文件目录的组织结构、一本书的目录：

这种结构类似于自然界中的树一样，从根里衍生出许多枝干，再从枝干中衍生出许多更小的枝干，最后衍生出更多的叶子。

---

树的概念和定义

树的定义

树(Tree)是n(n>=0)个结点的有限集。

​ 当n=0（即无结点）时，称为空树，空树是树的特例。
​ 当n>0时为非空树，对于非空树：

1. 必有且只有一个称之为根(Root)的结点。

2. 除根结点以外的n-1个结点可以划分为m个根的子树(SubTree)。

   

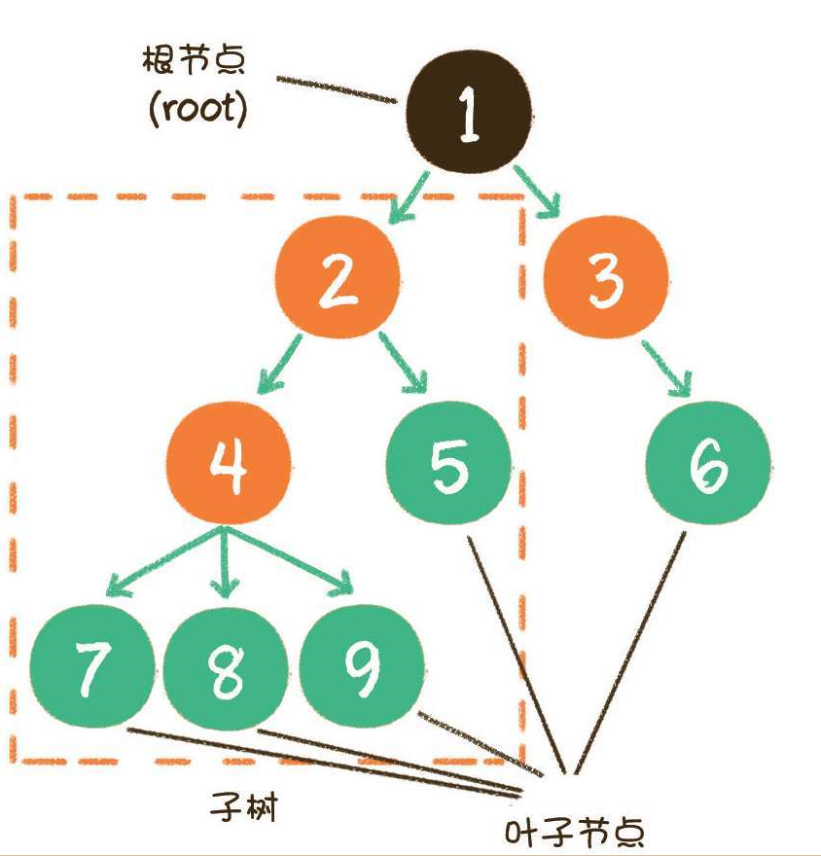
树其实也是一种递归的实现，即树的定义之中还用到了树的概念。

对比线性表和树的结构，他们有很大的不同。

线性结构	树结构
第一个数据元素：无前驱	根结点：无双亲，唯一
最后一个数据元素：无后继	叶结点：无孩子，可以多个
中间元素：一个前去一个后继	中间节点：一个双亲多个孩子

树的固有特性

• 非空树至少有一个结点，只有一个结点的树称为最小树，这个结点称为树的根结点或者简称为树根。

• 在含有多个结点的树中，除了根结点以外，其余的结点构成若干棵子树（一棵树是由若干个子树构成的），各子树间互不相交。

  

  图中的两个结构就不符合定义，因为他们都有相交的子树。

• 每颗子树除了根结点以外，每个节点有且只有一个直接前驱，但可以有0到多个直接后继。

树的基本术语

1. 结点：树中的一个个独立单元。包含一个数据元素和若干指向其他节点的分支信息。

2. 结点的度(De-gree)：一个结点的子树个数。

3. 树的度：树内各结点度的最大值。

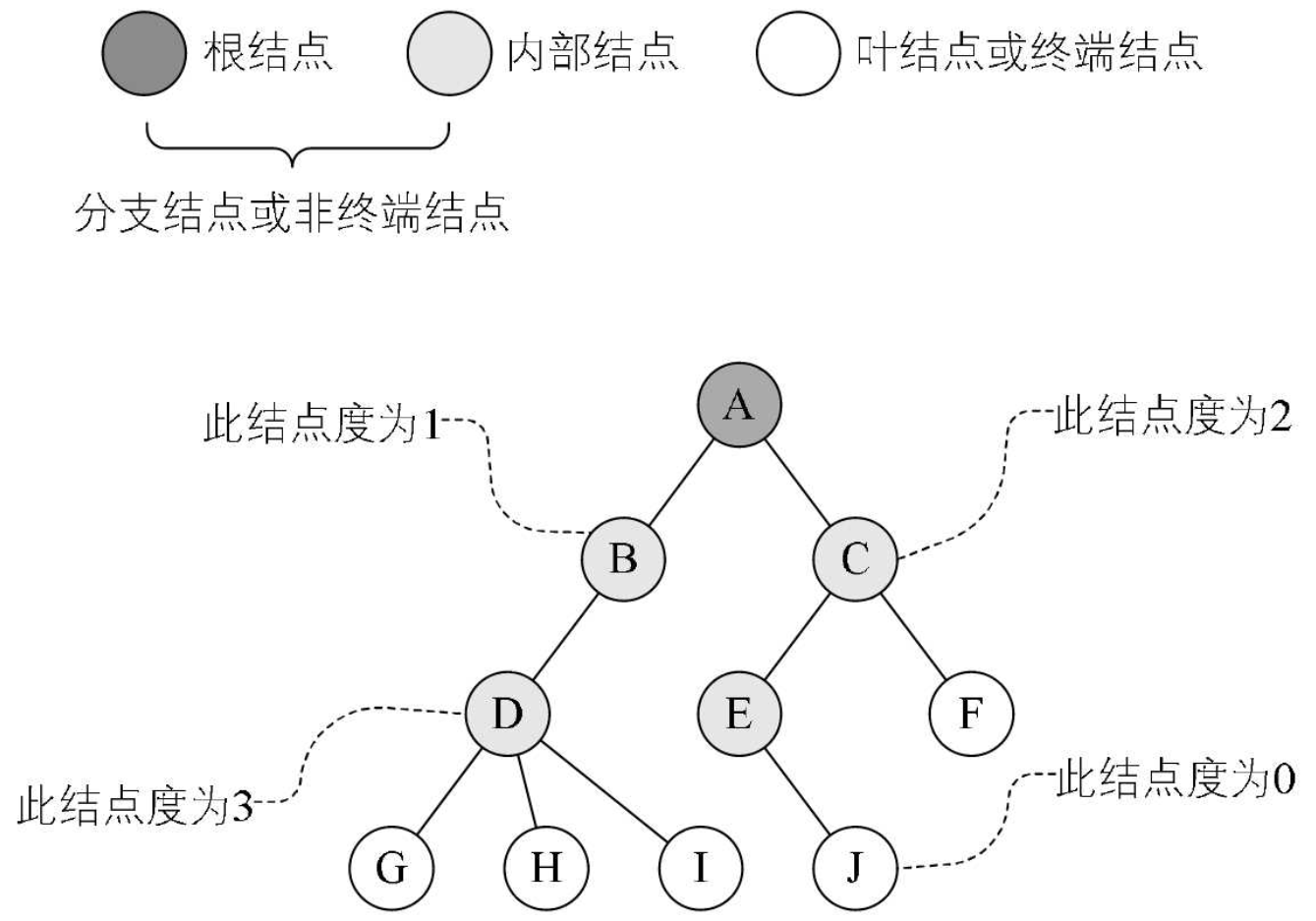
   因为这棵树结点的度的最大值是结点D的度，为3，所以树的度也为3。

4. 叶结点(Leaf)：度为0的节点，即无后继的结点称为叶结点或终端结点。

5. 分支结点：度不为0的结点，又称为非终端结点，除根结点外，非终端节点也称为内部节点。

6. 结点的层次(Level)：从根结点开始定义，根结点的层次为1，根的直接后继的层次为2，依此类推。

7. 结点的层序编号：将树中的结点按照从上到下，同层按照从左到右的次序排成一个线性序列，依次给他们编以从1开始的连续的自然数。

8. 树的高度/深度(Depth)：树中所有结点的层次的最大值，图中的树深度为4。

   
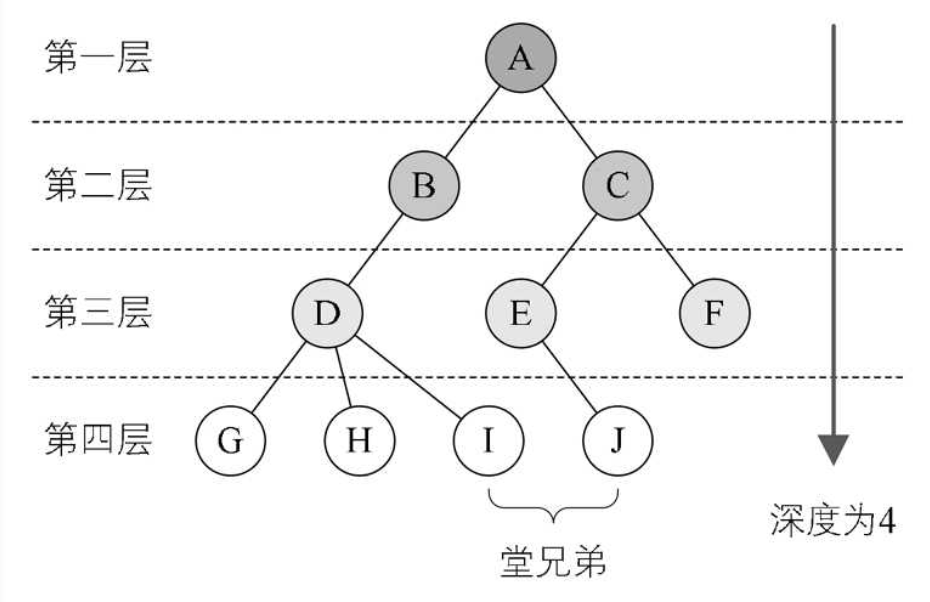
   • 空树的高度为0。
   • 只有根结点的树的高度为1。

9. 森林(Forest)：m（m>=0）棵互不相交的树的集合。对树中每个结点而言，其子树的集合即为森林。将一棵非空非最小树的树根结点删去，树就变成一个森林。

10. 孩子结点(Child)：一个结点的直接后继称为该结点的孩子节点。

11. 双亲结点(Parent)：一个结点的直接前驱称为该节点的双亲结点。

12. 兄弟结点(Sibling)：同一双亲结点的孩子之间互相称为兄弟结点。

13. 有序树：将树中结点的各子树看成从左到右是有先后次序的（不能互换），则称为有序树，否则称为无序树。

    ---

二叉树

二叉树的定义

满足以下两个条件的树形结构称为二叉树（Binary Tree）：

1. 每个结点最多有两棵子树（即不存在度大于2的结点）。

2. 二叉树的子树有左右之分，其次序不能任意颠倒，即使树中某结点只有一棵子树，也要区分它是左子树还是右子树。

   

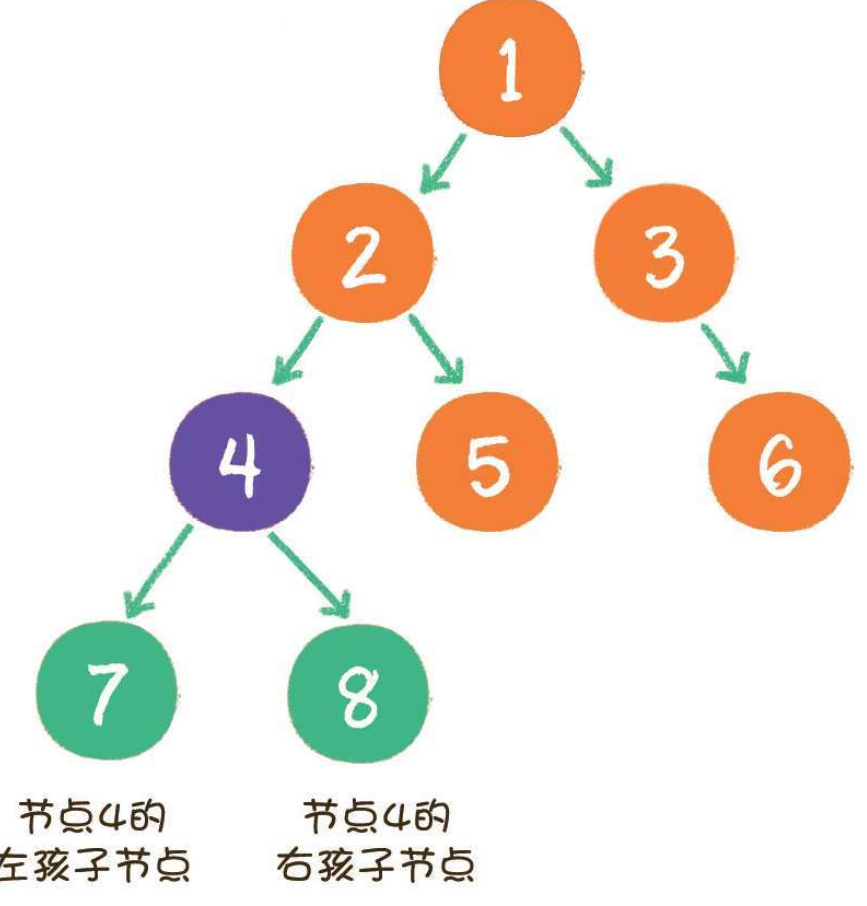
   二叉树结点的两个孩子结点，左边的被称为左孩子(Left child),右边的被称为右孩子(Right child)。两个孩子结点也有左右之分，次序不能任意颠倒。

二叉树的五种基本形态：

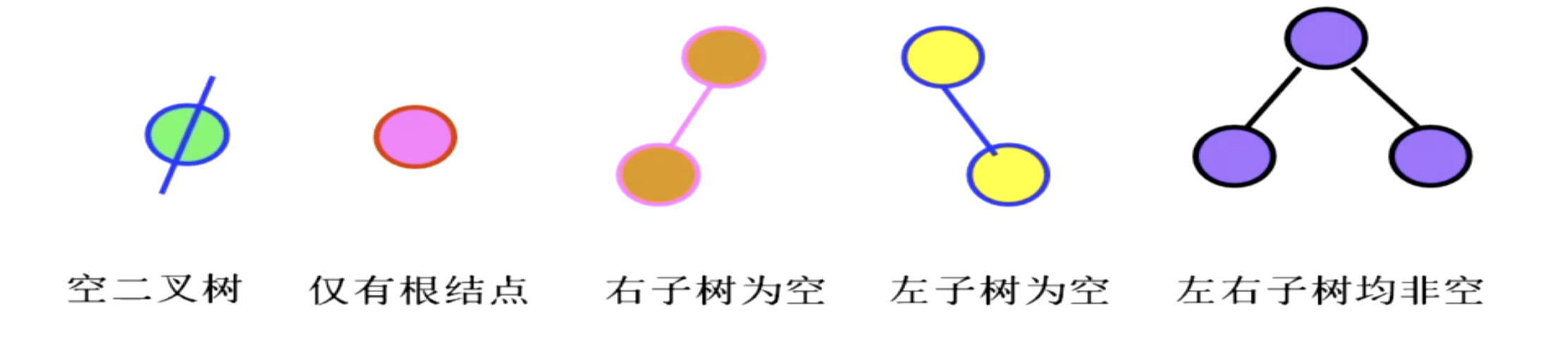
前面有关树的术语都适用于二叉树。

二叉树的性质

1. 在二叉树的第i层上（i从1开始计数）最多有2^i-1个结点（i>=1）。
2. 高度为k的二叉树最多有2^k-1个结点（k>=1）。
3. 具有n（n>=1）个结点的完全二叉树的高度最多为n，最少为(log₂n)+1。
4. 对任何一棵二叉树，如果其叶结点有n个，度为2的结点有m个，则有：n=m+1。
5. 如果对一棵有n个结点的完全二叉树（其深度为(log₂n)+1）的结点按层序编号（从第一层到(log₂n)+1层，每层从左到右），对任一结点i(1<=i<=n)有：
   • 如果i=1，则结点i是二叉树的根，无双亲（属实孤儿）；如果i>1，则其双亲是结点i/2。
   • 如果2i>n，则结点i无左孩子（结点i为叶子结点）；否则其左孩子是结点2i。
   • 如果2i+1>n，则结点i无右孩子；否则其右孩子是结点2i+1。
6. n个结点可以组成1/(n+1)*[(2n)!/(n!*n!)]种不同构的二叉树。

特殊二叉树

1. 满二叉树：在一棵二叉树中，如果所有分支（非叶子结点）都存在左子树和右子树，并且所有的叶子都在同一层上（高度为k的二叉树且有2^k-1个结点）。

   说白了就是每个分支都是满的。

   

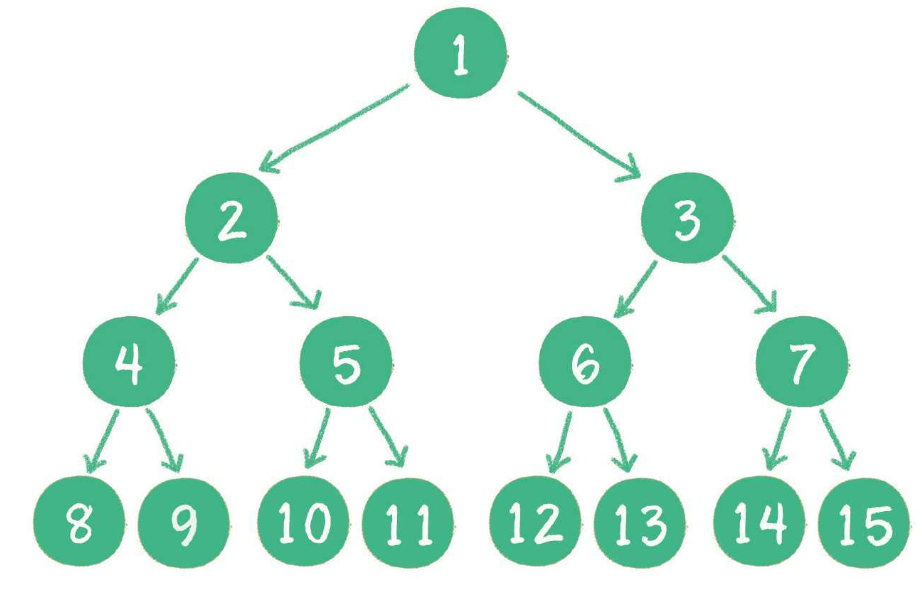
2. 完全二叉树：把一棵具有n个结点的二叉树按层序编号，如果编号为i(1<=i<=n)的结点和同样深度的满二叉树中编号i的节点在二叉树中位置完全相同，那么这棵二叉树被称为完全二叉树。也可以理解为把一棵满二叉树的最后一层结点，从左向右连续却掉若干个结点，那么它就是完全二叉树。

   

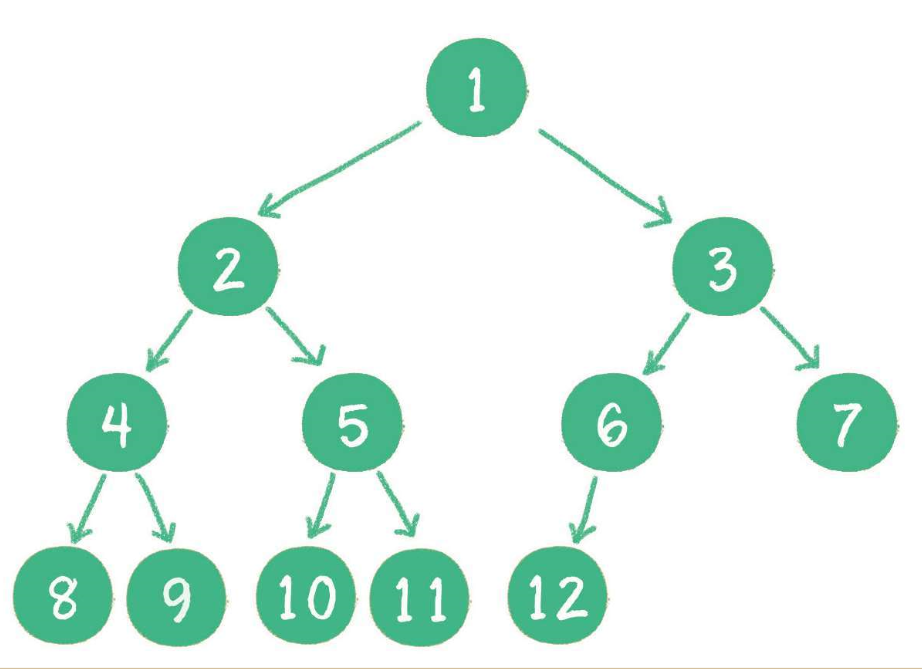
   （可以看到这个二叉树编号从1到12的12个结点和上图的二叉树的12个结点的位置完全对应，所以这个树是完全二叉树。)

   满二叉树一定是完全二叉树，但完全二叉树不一定是满二叉树。

   在完全二叉树或满二叉树中，如果某个结点没有左儿子，那么他一定没有右儿子（即该结点是一个叶结点）。