从零开始游戏开发——2.3 欧拉角与四元数
在2.2矩阵章节讲到可以将坐标空间的基向量使用矩阵来表示,从而可以用3x3的矩阵来表达物体的方位,并且使用矩阵表示方位也是图形API使用的形式。但3x3的旋转矩阵需要存储9个数据,相比较欧拉角和四元数,内存占用会比较大,并且表达并不直观。
欧拉角可以使用3个数来表达方位,欧拉角使用Roll-Pitch-Yaw 或 Heading-Pitch-Bank的命名约定可以用来表示物体绕各个坐标轴的旋转。在我们实现中,并不打算写一个欧拉角的类,而是直接使用Vector3来存储欧拉角绕x、y、z的旋转。欧拉角在开发中对于程序调试非方便,但欧拉角本身也存在一定的缺点,首先欧拉角有万向锁的问题,即我们先绕y轴进行水平方向的旋转,再绕x轴进行垂直方向的旋转,而这时旋转了90度,则当绕z轴旋转时,旋转的方位仍然是在水平方向,在这种情况丢失了一个旋转维度。另外一点就是欧拉角表示方位的方式不唯一,即绕x轴旋转theta度和这个角度加上n * 360度表示的是同一个方位,这可能会对我们方向的插值造成困扰。
四元数使用4个数来表示绕轴v旋转theta度的方位,在使用四元数表示方位时,类似于向量表示方向的单位向量, 我们使用的是单位四元数,即四元数||q|| = 1,因此四元数中并不是直接存储了旋转角度theta和旋转轴,而是以
q = [cos(θ/2) sin(θ/2)nx sin(θ/2)ny sin(θ/2)nz]
这种形式来存储数据,使用单位四元数时,他的四元数的逆等于四元数的共轭:
q-1 = q*/||q|| = q* = [w -v]
这样就可以使用共轭来表示相反的方位角。四元数主要包含了下面的操作:
1 template<typename T> 2 class Quaternion 3 { 4 public: 5 Quaternion(); 6 Quaternion(T w, T x, T y, T z); 7 8 void Identity(); 9 void Normalize(); 10 11 Vector3<T> ToEulerAngle(); 12 Quaternion &FromEulerAngle(T x, T y, T z); 13 14 Quaternion &MakeRotateByX(T theta); 15 Quaternion &MakeRotateByY(T theta); 16 Quaternion &MakeRotateByZ(T theta); 17 Quaternion &MakeRotateByAxis(const Vector3<T> &axis, T theta); 18 T GetRotationAngle() const; 19 Vector3<T> GetRotationAxis() const; 20 21 Quaternion operator*(const Quaternion &q) const; 22 Vector3<T> operator*(const Vector3<T> &v) const; 23 24 static Quaternion Slerp(const Quaternion &q0, const Quaternion &q1, float t); 25 26 template <typename T1> 27 friend ostream &operator<<(ostream &out, const Quaternion<T1> &q); 28 private: 29 T w, x, y, z; 30 };
第11行~12行声明了四元数与欧拉角之间的转换,第14~17行则是以四元数的形式声明绕各轴旋转,第21~22行声明了四元数和乘法操作,四元数之前的乘法与矩阵乘法类似,可以将多个旋转操作连接为一个四元数,四元数与向量相乘则是对用来旋转向量的。
第24行的Slerp操作是对四元数的球面插值。上面代码的具体实现代码如下:
1 template <typename T> 2 Quaternion<T>::Quaternion() 3 :w(1), x(0), y(0), z(0) 4 { 5 } 6 7 template <typename T> 8 Quaternion<T>::Quaternion(T w, T x, T y, T z) 9 :w(w), x(x), y(y), z(z) 10 { 11 } 12 13 template <typename T> 14 void Quaternion<T>::Identity() 15 { 16 w = static_cast<T>(1); 17 x = y = z = static_cast<T>(0); 18 } 19 20 template <typename T> 21 void Quaternion<T>::Normalize() 22 { 23 T mag = (T)sqrt(w * w + x * x + y * y + z * z); 24 25 if (mag > 0) 26 { 27 T oneOverMag = (T)1 / mag; 28 w *= oneOverMag; 29 x *= oneOverMag; 30 y *= oneOverMag; 31 z *= oneOverMag; 32 } 33 else 34 { 35 assert(false); 36 Identity(); 37 } 38 } 39 40 template <typename T> 41 Vector3<T> Quaternion<T>::ToEulerAngle() 42 { 43 Vector3<T> euler; 44 Quaternion &q = *this; 45 T sp = (T)-2 * (q.y * q.z - q.w * q.x); 46 if (fabs(sp) > (T)0.9999) 47 { 48 euler.y = PI_DIV_2 * sp; 49 euler.x = atan2(-q.x + q.z + q.w * q.y, (T)0.5 - q.y * q.y - q.z * q.z); 50 euler.z = 0; 51 } 52 else 53 { 54 euler.y = asin(sp); 55 euler.x = atan2(q.x * q.z + q.w * q.y, (T)0.5 - q.x * q.x - q.y * q.y); 56 euler.z = atan2(q.x * q.y + q.w * q.z, (T)0.5 - q.x * q.x - q.z * q.z); 57 } 58 59 return euler; 60 } 61 62 template <typename T> 63 Quaternion<T> &Quaternion<T>::FromEulerAngle(T x, T y, T z) 64 { 65 T hOver2 = (T)0.5 * y; 66 T pOver2 = (T)0.5 * x; 67 T bOver2 = (T)0.5 * z; 68 69 T sh, sp, sb; 70 T ch, cp, cb; 71 72 sh = sin(hOver2); 73 ch = cos(hOver2); 74 sp = sin(pOver2); 75 cp = cos(pOver2); 76 sb = sin(bOver2); 77 cb = cos(bOver2); 78 79 this->w = ch * cp * cb + sh * sp * sb; 80 this->x = ch * sp * cb + sh * cp * sb; 81 this->y = -ch * sp * sb + sh * cp * cb; 82 this->z = -sh * sp * cb + ch * cp * sb; 83 84 return *this; 85 } 86 87 template <typename T> 88 Quaternion<T> Quaternion<T>::operator*(const Quaternion<T> &q) const 89 { 90 //右乘 91 return Quaternion(w * q.w - x * q.x - y * q.y - z * q.z, 92 w * q.x + x * q.w + z * q.y - y * q.z, 93 w * q.y + y * q.w + x * q.z - z * q.x, 94 w * q.z + z * q.w + y * q.x - x * q.y); 95 } 96 97 template <typename T> 98 Vector3<T> Quaternion<T>::operator*(const Vector3<T> &v) const 99 { 100 Quaternion vq(0, v.x, v.y, v.z); 101 Quaternion invQ(w, -x, -y, -z); 102 Quaternion result = invQ * vq * *this; 103 104 return Vector3<T>(result.x, result.y, result.z); 105 } 106 107 template <typename T> 108 Quaternion<T> &Quaternion<T>::MakeRotateByX(T theta) 109 { 110 T thetaOver2 = theta * (T)0.5; 111 112 w = cos(thetaOver2); 113 x = sin(thetaOver2); 114 y = 0; 115 z = 0; 116 return *this; 117 } 118 119 template <typename T> 120 Quaternion<T> &Quaternion<T>::MakeRotateByY(T theta) 121 { 122 T thetaOver2 = theta * (T)0.5; 123 124 w = cos(thetaOver2); 125 x = 0; 126 y = sin(thetaOver2); 127 z = 0; 128 return *this; 129 } 130 template <typename T> 131 Quaternion<T> &Quaternion<T>::MakeRotateByZ(T theta) 132 { 133 T thetaOver2 = theta * (T)0.5; 134 135 w = cos(thetaOver2); 136 x = 0; 137 y = 0; 138 z = sin(thetaOver2); 139 return *this; 140 } 141 template <typename T> 142 Quaternion<T> &Quaternion<T>::MakeRotateByAxis(const Vector3<T> &axis, T theta) 143 { 144 Vector3<T> axisNormallize = axis; 145 axisNormallize.Normalize(); 146 147 T thetaOver2 = theta * (T)0.5; 148 T sinThetaOver2 = sin(thetaOver2); 149 150 w = cos(thetaOver2); 151 x = axisNormallize.x * sinThetaOver2; 152 y = axisNormallize.y * sinThetaOver2; 153 z = axisNormallize.z * sinThetaOver2; 154 return *this; 155 } 156 157 template <typename T> 158 T Quaternion<T>::GetRotationAngle() const 159 { 160 T thetaOver2; 161 if (w <= (T)-1) 162 thetaOver2 = PI; 163 else if (w >= (T)1) 164 thetaOver2 = 0; 165 else 166 thetaOver2 = acos(w); 167 return thetaOver2 * (T)2; 168 } 169 170 template <typename T> 171 Vector3<T> Quaternion<T>::GetRotationAxis() const 172 { 173 T sinThetaOver2Sq = (T)1 - w * w; 174 if (sinThetaOver2Sq <= 0) 175 { 176 return Vector3<T>(1, 0, 0); 177 } 178 179 T oneOverSinThetaOver2 = (T)1 / sqrt(sinThetaOver2Sq); 180 return Vector3<T>(x * oneOverSinThetaOver2, y * oneOverSinThetaOver2, z * oneOverSinThetaOver2); 181 } 182 183 template <typename T> 184 Quaternion<T> Quaternion<T>::Slerp(const Quaternion &q0, const Quaternion &q1, float t) 185 { 186 if (t <= 0) return q0; 187 if (t >= (T)1) return q1; 188 189 T cosOmega = q0.w * q1.w + q0.x * q1.x + q0.y * q1.y + q0.z * q1.z; 190 T q1w = q1.w; 191 T q1x = q1.x; 192 T q1y = q1.y; 193 T q1z = q1.z; 194 if (cosOmega < 0) 195 { 196 q1w = -q1w; 197 q1x = -q1x; 198 q1y = -q1y; 199 q1z = -q1z; 200 cosOmega = -cosOmega; 201 } 202 203 assert(cosOmega < 1); 204 205 T k0, k1; 206 if (cosOmega > (T)0.9999) 207 { 208 k0 = (T)1 - t; 209 k1 = t; 210 } 211 else 212 { 213 T sinOmega = sqrt((T)1 - cosOmega * cosOmega); 214 T omega = atan2(sinOmega, cosOmega); 215 T oneOverSinOmega = (T)1 / sinOmega; 216 k0 = sin(((T)(1) - t) * omega) * oneOverSinOmega; 217 k1 = sin(t * omega) * oneOverSinOmega; 218 } 219 220 return Quaternion( 221 k0 * q0.w + k1 * q1w, 222 k0 * q0.x + k1 * q1x, 223 k0 * q0.y + k1 * q1y, 224 k0 * q0.z + k1 * q1z); 225 } 226 227 template <typename T> 228 ostream &operator<<(ostream &out, const Quaternion<T> &q) 229 { 230 out << q.w << "," << q.x << "," << q.y << "," << q.z; 231 return out; 232 }
具体实现都比较简单,这里重点讲一下Slerp操作,先以向量为类,如下图所示:
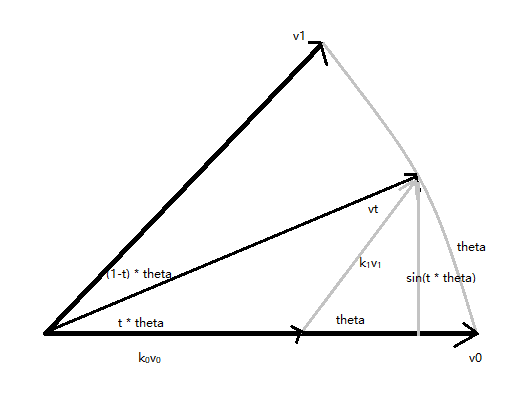
向量vt = k0v0 + k1v1,这里只需要求出k0和k1即可,由以k1v1为斜边的直角三角形可知:
sin(theta) = sin(t * theta) / k1,
则:
k1 = sin(t * theta) / sin(theta),
同理:
k0 = sin((1-t) * theta) / sin(theta),
将向量的Slerp操作扩展到四元数即得到了四元数的球面插值操作:
Slerp(q0, q1, t) = k1q0 + k1q1
参考文献:
3D数学基础:图形与游戏开发
本文来自博客园,作者:毅安,转载请注明原文链接:https://www.cnblogs.com/primarycode/p/16438709.html,文章内容同步更新微信公众号:“游戏开发实战”或“GamePrimaryCode”


