从零开始游戏开发——2.2 矩阵

　　在游戏开发中，矩阵具有十分重要的地位，但他也只是我们操作点和向量的一个工具，在这里我们使用列优先规则来存储矩阵。在这里矩阵最主要的两个作用是：1. 旋转一个向量或者变换一个坐标点的位置；2. 坐标空间变换。对于第一点，在第2.1向量章节中，我们直接使用了三角函数对向量进行旋转，矩阵则是提供了另一种表示方式。我们知道向量可以表示为坐标空间基向量和的形式，即向量p = ax + by + cz = (1, 0, 0)*a + (0, 1, 0)*b + (0, 0, 1) * c，(a, b, c)就是向量p在x, y, z空间中的坐标如下图，

 

 

 

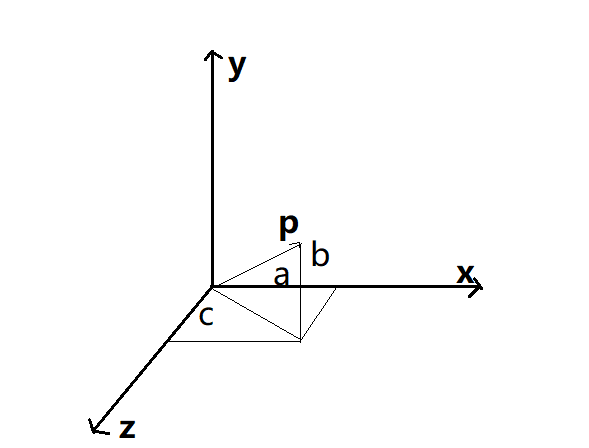
 上面表达式可以写成矩阵相乘的形式：

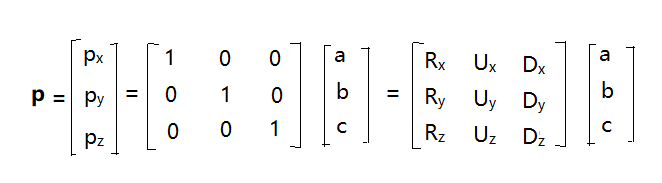
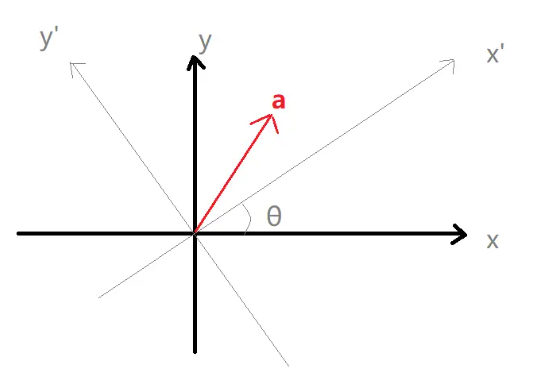
我们让x、y坐标轴绕z旋转到x'、y'如上图，x'、y'的基向量分别为(cosθ, sinθ, 0)和(-sinθ, cosθ, 0)，替换上面的公式的RUD基向量，即得到绕z轴旋转的矩阵为：

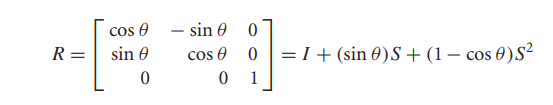
 其中

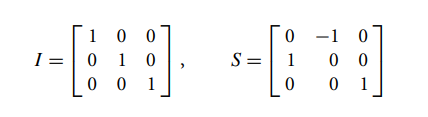
 同理可以得到绕y轴的矩阵为：

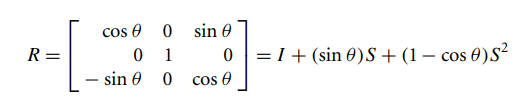 ，其中

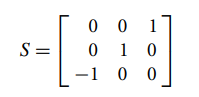
 绕x轴的矩阵为：

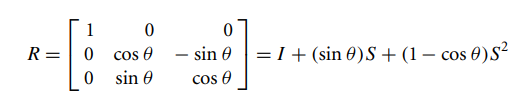 ，其中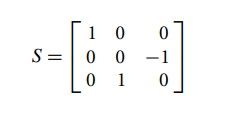 

当绕任意向量u旋转时，

 

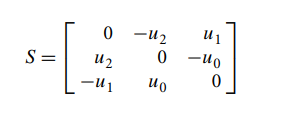
 则此时旋转矩阵为：

 

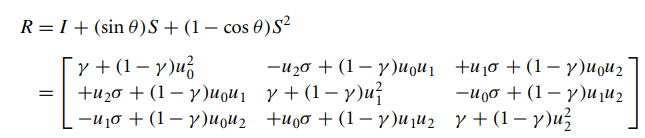
也可以利用矩阵来计算反射矩阵，根据向量的反射可以得到：

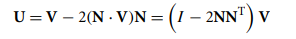
从而得到反射矩阵如下（在《3D游戏引擎设计》一书中，此矩阵有些错误这里进行了修正）：

 

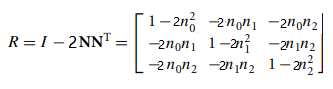
　　利用矩阵来计算缩放则比较简单，对3x3的矩阵M来讲，只需要将M(0,0)、M(1,1)、M(2,2)矩阵位置处的值进行缩放，即可对向量x,y,z方向进行缩放。上面利用3x3矩阵计算了出了旋转矩阵，当要对空间点位置进行移动时，需要用到矩阵和向量的第四维，此时的向量称为齐次坐标，此时的矩阵形式如下：

矩阵中的(b0, b1, b2)即为在x、y、z方向的偏移。用了这个4x4的矩阵，可以将向量从一个坐标空间转换到另一个坐标空间，这在渲染中是最常用的操作。在美术设计师给到一个模型时，模型中点的位置是相对于模型自己的坐标空间，而游戏世界需要渲染一个模型，会将整个模型放置于世界中的某个位置并带有旋转和缩放，游戏世界所在的空间为世界空间，要渲染一个模型，还需要一个摄像机和投影平面，通过摄像机去看一个物体是需要转换到相机空间的，最后还需要投影到摄像机的近裁剪面，在这里模型转换到世界空间的矩阵为M，世界空间转换到相机空间矩阵为V，相机空间进行投影计算矩阵为P，这就是以后会常听到的MVP矩阵。要真正渲染一个顶点Q，由于矩阵是列优先的，利用矩阵乘法计算坐标空间转换为右乘计算Q' = P * V * M * Q。这些用到的矩阵的实现，会在后面章节详细介绍。下面是4x4矩阵的实现代码：

#ifndef _MATRIX_4_X_4_HPP
#define _MATRIX_4_X_4_HPP

#include "Vector3.hpp"

using namespace std;
template <typename T>
class Matrix4x4
{
public:
    Matrix4x4(
            T m00, T m01, T m02, T m03,
            T m10, T m11, T m12, T m13,
            T m20, T m21, T m22, T m23,
            T m30, T m31, T m32, T m33
    );
    Matrix4x4(T m[16]);
    Matrix4x4();

    Matrix4x4 &MakeIdentity();
    void MakeRotation(const Vector3<T> &v, T radian);
    void MakeTransition(const Vector3<T> & v);
    void MakeTransition(T x, T y, T z);
    void MakeScale(const Vector3<T> & v);
    void MakeScale(T x, T y, T z);
    void MakeReflect(const Vector3<T> &normal);
    bool GetInverse(Matrix4x4<T> &out) const;
    void GetTransposed(Matrix4x4<T> &o) const;
    Vector3<T> Transform(const Vector3<T> &v) const;
    Matrix4x4<T> operator*(const Matrix4x4 &m) const;
    T operator[](int i) const;
    T operator[](int i);
    T operator()(int row, int col) const;
    T operator()(int row, int col);

    union
    {
        struct
        {
            T m00, m01, m02, m03;
            T m10, m11, m12, m13;
            T m20, m21, m22, m23;
            T m30, m31, m32, m33;
        };

        T m[16];     
    };
};


template <typename T>
Matrix4x4<T>::Matrix4x4(
        T m00, T m01, T m02, T m03,
        T m10, T m11, T m12, T m13,
        T m20, T m21, T m22, T m23,
        T m30, T m31, T m32, T m33
):m00(m00), m01(m01), m02(m02), m03(m03),
    m10(m10), m11(m11), m12(m12), m13(m13),
    m20(m20), m21(m21), m22(m22), m23(m23),
    m30(m30), m31(m31), m32(m32), m33(m33)
{
}

template <typename T>
Matrix4x4<T>::Matrix4x4(T m[16])
{
    memcpy(this->m, m, sizeof(this->m));
}

template <typename T>
Matrix4x4<T>::Matrix4x4()
    : m00(1), m01(0), m02(0), m03(0),
        m10(0), m11(1), m12(0), m13(0),
        m20(0), m21(0), m22(1), m23(0),
        m30(0), m31(0), m32(0), m33(1)
{
}


template <typename T>
Matrix4x4<T> &Matrix4x4<T>::MakeIdentity()
{
    memset(m, 0, sizeof(m));
    m[0] = m[5] = m[10] = m[15] = static_cast<T>(1);
    return *this;
}


template <typename T>
void Matrix4x4<T>::MakeRotation(const Vector3<T> &v, T radian)
{
    T c = cos(radian);
    T s = sin(radian);
    T x2 = v.x * v.x;
    T y2 = v.y * v.y;
    T z2 = v.z * v.z;
    T xy = v.x * v.y;
    T xz = v.x * v.z;
    T yz = v.y * v.z;

    m00 = c + (1 - c) * x2;         m01 = -v.z * s + (1 - c) * xy;      m02 = v.y * s + (1 - c) * xz;
    m10 = v.z * s + (1 - c) * xy;   m11 = c + (1 - c) * y2;             m12 = -v.x * s + (1 - c) * yz;
    m20 = -v.y * s + (1 - c) * xz;  m21 = v.x * s + (1 - c) * yz;       m22 = c + (1 - c) * z2;
}

template <typename T>
void Matrix4x4<T>::MakeTransition(const Vector3<T> & v)
{
    m03 = v.x;
    m13 = v.y;
    m23 = v.z;
}

template <typename T>
void Matrix4x4<T>::MakeTransition(T x, T y, T z)
{
    m03 = x;
    m13 = y;
    m23 = z;
}

template <typename T>
void Matrix4x4<T>::MakeScale(T x, T y, T z)
{
    m00 = x;
    m11 = y;
    m22 = z;
}

template <typename T>
void Matrix4x4<T>::MakeScale(const Vector3<T> &v)
{
    m00 = v.x;
    m11 = v.y;
    m22 = v.z;
}

template <typename T>
void Matrix4x4<T>::MakeReflect(const Vector3<T> &n)
{
    T x2 = n.x * n.x;
    T y2 = n.y * n.y;
    T z2 = n.z * n.z;

    T xy = n.x * n.y;
    T xz = n.x * n.z;
    T yz = n.y * n.z;

    m00 = 1 - 2 * x2;       m01 = -2 * xy;      m02 = -2 * xz;
    m10 = -2 * xy;          m11 = 1 - 2 * y2;   m12 = -2 * yz;
    m20 = -2 * xz;          m21 = -2 * yz;      m22 = 1 - 2 * z2;
}

template <typename T>
bool Matrix4x4<T>::GetInverse(Matrix4x4<T> &out) const
{
    const Matrix4x4 &m = *this;

    T d = (m(0, 0) * m(1, 1) - m(0, 1) * m(1, 0)) * (m(2, 2) * m(3, 3) - m(2, 3) * m(3, 2)) -
              (m(0, 0) * m(1, 2) - m(0, 2) * m(1, 0)) * (m(2, 1) * m(3, 3) - m(2, 3) * m(3, 1)) +
              (m(0, 0) * m(1, 3) - m(0, 3) * m(1, 0)) * (m(2, 1) * m(3, 2) - m(2, 2) * m(3, 1)) +
              (m(0, 1) * m(1, 2) - m(0, 2) * m(1, 1)) * (m(2, 0) * m(3, 3) - m(2, 3) * m(3, 0)) -
              (m(0, 1) * m(1, 3) - m(0, 3) * m(1, 1)) * (m(2, 0) * m(3, 2) - m(2, 2) * m(3, 0)) +
              (m(0, 2) * m(1, 3) - m(0, 3) * m(1, 2)) * (m(2, 0) * m(3, 1) - m(2, 1) * m(3, 0));

    if (d > -0.00001 && d < 0.00001)
        return false;

    d = 1 / d;

    out(0, 0) = d * (m(1, 1) * (m(2, 2) * m(3, 3) - m(2, 3) * m(3, 2)) +
                     m(1, 2) * (m(2, 3) * m(3, 1) - m(2, 1) * m(3, 3)) +
                     m(1, 3) * (m(2, 1) * m(3, 2) - m(2, 2) * m(3, 1)));
    out(0, 1) = d * (m(2, 1) * (m(0, 2) * m(3, 3) - m(0, 3) * m(3, 2)) +
                     m(2, 2) * (m(0, 3) * m(3, 1) - m(0, 1) * m(3, 3)) +
                     m(2, 3) * (m(0, 1) * m(3, 2) - m(0, 2) * m(3, 1)));
    out(0, 2) = d * (m(3, 1) * (m(0, 2) * m(1, 3) - m(0, 3) * m(1, 2)) +
                     m(3, 2) * (m(0, 3) * m(1, 1) - m(0, 1) * m(1, 3)) +
                     m(3, 3) * (m(0, 1) * m(1, 2) - m(0, 2) * m(1, 1)));
    out(0, 3) = d * (m(0, 1) * (m(1, 3) * m(2, 2) - m(1, 2) * m(2, 3)) +
                     m(0, 2) * (m(1, 1) * m(2, 3) - m(1, 3) * m(2, 1)) +
                     m(0, 3) * (m(1, 2) * m(2, 1) - m(1, 1) * m(2, 2)));
    out(1, 0) = d * (m(1, 2) * (m(2, 0) * m(3, 3) - m(2, 3) * m(3, 0)) +
                     m(1, 3) * (m(2, 2) * m(3, 0) - m(2, 0) * m(3, 2)) +
                     m(1, 0) * (m(2, 3) * m(3, 2) - m(2, 2) * m(3, 3)));
    out(1, 1) = d * (m(2, 2) * (m(0, 0) * m(3, 3) - m(0, 3) * m(3, 0)) +
                     m(2, 3) * (m(0, 2) * m(3, 0) - m(0, 0) * m(3, 2)) +
                     m(2, 0) * (m(0, 3) * m(3, 2) - m(0, 2) * m(3, 3)));
    out(1, 2) = d * (m(3, 2) * (m(0, 0) * m(1, 3) - m(0, 3) * m(1, 0)) +
                     m(3, 3) * (m(0, 2) * m(1, 0) - m(0, 0) * m(1, 2)) +
                     m(3, 0) * (m(0, 3) * m(1, 2) - m(0, 2) * m(1, 3)));
    out(1, 3) = d * (m(0, 2) * (m(1, 3) * m(2, 0) - m(1, 0) * m(2, 3)) +
                     m(0, 3) * (m(1, 0) * m(2, 2) - m(1, 2) * m(2, 0)) +
                     m(0, 0) * (m(1, 2) * m(2, 3) - m(1, 3) * m(2, 2)));
    out(2, 0) = d * (m(1, 3) * (m(2, 0) * m(3, 1) - m(2, 1) * m(3, 0)) +
                     m(1, 0) * (m(2, 1) * m(3, 3) - m(2, 3) * m(3, 1)) +
                     m(1, 1) * (m(2, 3) * m(3, 0) - m(2, 0) * m(3, 3)));
    out(2, 1) = d * (m(2, 3) * (m(0, 0) * m(3, 1) - m(0, 1) * m(3, 0)) +
                     m(2, 0) * (m(0, 1) * m(3, 3) - m(0, 3) * m(3, 1)) +
                     m(2, 1) * (m(0, 3) * m(3, 0) - m(0, 0) * m(3, 3)));
    out(2, 2) = d * (m(3, 3) * (m(0, 0) * m(1, 1) - m(0, 1) * m(1, 0)) +
                     m(3, 0) * (m(0, 1) * m(1, 3) - m(0, 3) * m(1, 1)) +
                     m(3, 1) * (m(0, 3) * m(1, 0) - m(0, 0) * m(1, 3)));
    out(2, 3) = d * (m(0, 3) * (m(1, 1) * m(2, 0) - m(1, 0) * m(2, 1)) +
                     m(0, 0) * (m(1, 3) * m(2, 1) - m(1, 1) * m(2, 3)) +
                     m(0, 1) * (m(1, 0) * m(2, 3) - m(1, 3) * m(2, 0)));
    out(3, 0) = d * (m(1, 0) * (m(2, 2) * m(3, 1) - m(2, 1) * m(3, 2)) +
                     m(1, 1) * (m(2, 0) * m(3, 2) - m(2, 2) * m(3, 0)) +
                     m(1, 2) * (m(2, 1) * m(3, 0) - m(2, 0) * m(3, 1)));
    out(3, 1) = d * (m(2, 0) * (m(0, 2) * m(3, 1) - m(0, 1) * m(3, 2)) +
                     m(2, 1) * (m(0, 0) * m(3, 2) - m(0, 2) * m(3, 0)) +
                     m(2, 2) * (m(0, 1) * m(3, 0) - m(0, 0) * m(3, 1)));
    out(3, 2) = d * (m(3, 0) * (m(0, 2) * m(1, 1) - m(0, 1) * m(1, 2)) +
                     m(3, 1) * (m(0, 0) * m(1, 2) - m(0, 2) * m(1, 0)) +
                     m(3, 2) * (m(0, 1) * m(1, 0) - m(0, 0) * m(1, 1)));
    out(3, 3) = d * (m(0, 0) * (m(1, 1) * m(2, 2) - m(1, 2) * m(2, 1)) +
                     m(0, 1) * (m(1, 2) * m(2, 0) - m(1, 0) * m(2, 2)) +
                     m(0, 2) * (m(1, 0) * m(2, 1) - m(1, 1) * m(2, 0)));

    return true;
}

template <typename T>
void Matrix4x4<T>::GetTransposed(Matrix4x4<T> &o) const
{
    o[0] = m[0];
    o[1] = m[4];
    o[2] = m[8];
    o[3] = m[12];

    o[4] = m[1];
    o[5] = m[5];
    o[6] = m[9];
    o[7] = m[13];

    o[8] = m[2];
    o[9] = m[6];
    o[10] = m[10];
    o[11] = m[14];

    o[12] = m[3];
    o[13] = m[7];
    o[14] = m[11];
    o[15] = m[15];
}

template <typename T>
Vector3<T> Matrix4x4<T>::Transform(const Vector3<T> &v) const
{
    T w = (m30 * v.x + m31 * v.y + m32 * v.z + m33);
    T invW = w > 0 ? static_cast<T>(1.0) / w : static_cast<T>(1.0);
    return Vector3<T>(
        (m00 * v.x + m01 * v.y + m02 * v.z + m03) * invW,
        (m10 * v.x + m11 * v.y + m12 * v.z + m13) * invW,
        (m20 * v.x + m21 * v.y + m22 * v.z + m23) * invW
    );
}

template <typename T>
Matrix4x4<T> Matrix4x4<T>::operator*(const Matrix4x4<T> &m) const
{
    return Matrix4x4<T>(
        m00 * m.m00 + m01 * m.m10 + m02 * m.m20 + m03 * m.m30,
        m00 * m.m01 + m01 * m.m11 + m02 * m.m21 + m03 * m.m31,
        m00 * m.m02 + m01 * m.m12 + m02 * m.m22 + m03 * m.m32,
        m00 * m.m03 + m01 * m.m13 + m02 * m.m23 + m03 * m.m33,

        m10 * m.m00 + m11 * m.m10 + m12 * m.m20 + m13 * m.m30,
        m10 * m.m01 + m11 * m.m11 + m12 * m.m21 + m13 * m.m31,
        m10 * m.m02 + m11 * m.m12 + m12 * m.m22 + m13 * m.m32,
        m10 * m.m03 + m11 * m.m13 + m12 * m.m23 + m13 * m.m33,

        m20 * m.m00 + m21 * m.m10 + m22 * m.m20 + m23 * m.m30,
        m20 * m.m01 + m21 * m.m11 + m22 * m.m21 + m23 * m.m31,
        m20 * m.m02 + m21 * m.m12 + m22 * m.m22 + m23 * m.m32,
        m20 * m.m03 + m21 * m.m13 + m22 * m.m23 + m23 * m.m33,

        m30 * m.m00 + m31 * m.m10 + m32 * m.m20 + m33 * m.m30,
        m30 * m.m01 + m31 * m.m11 + m32 * m.m21 + m33 * m.m31,
        m30 * m.m02 + m31 * m.m12 + m32 * m.m22 + m33 * m.m32,
        m30 * m.m03 + m31 * m.m13 + m32 * m.m23 + m33 * m.m33
    );
}

template <typename T>
T Matrix4x4<T>::operator[](int i) const
{
    assert(i >= 0 && i < 16);
    return m[i];
}

template <typename T>
T Matrix4x4<T>::operator[](int i)
{
    assert(i >= 0 && i < 16);
    return m[i];
}


template <typename T>
T Matrix4x4<T>::operator()(int row, int col) const
{
    assert(row >=0 && row < 4 && col >= 0 && row < 4);
    return row << 2 + col;
}
template <typename T>
T Matrix4x4<T>::operator()(int row, int col)
{
    assert(row >=0 && row < 4 && col >= 0 && row < 4);
    return row << 2 + col;
}

template <typename T>
ostream &operator<<(ostream &out, const Matrix4x4<T> &m)
{
    for (int i = 0; i < 16; ++i)
    {
        out << m[i];
        if ((i + 1) % 4 == 0)
            out << endl;
        else if (i != 15)
            out << ",";

    }
    return out;
}

typedef Matrix4x4<float> Matrix4x4f;
typedef Matrix4x4<double> Matrix4x4d;

#endif

参考文献：

《3D数学基础：图形与游戏开发》

《3D游戏与计算机图形学中的数学方法》

《3D游戏引擎设计：实时计算机图形学的应用方法》