从零开始游戏开发——2.1 向量

　　在介绍向量前，首先要介绍下坐标系统，因为向量是依赖于坐标系统的，最常用的是笛卡尔直角坐标系。坐标系分为左手坐标系和右手坐标系，如下图，当我们使用向量[a,b,c]来做为我们的坐标系时，使用的是右手坐标系，而使用[c,b,a] 做为坐标系时，则使用了左手坐标系统，即两个基向量进行叉乘a x b = c时使用的是右手坐标系，而c x b = -a则使用的是左手坐标系。我们这里使用的是右手坐标系。

 

 

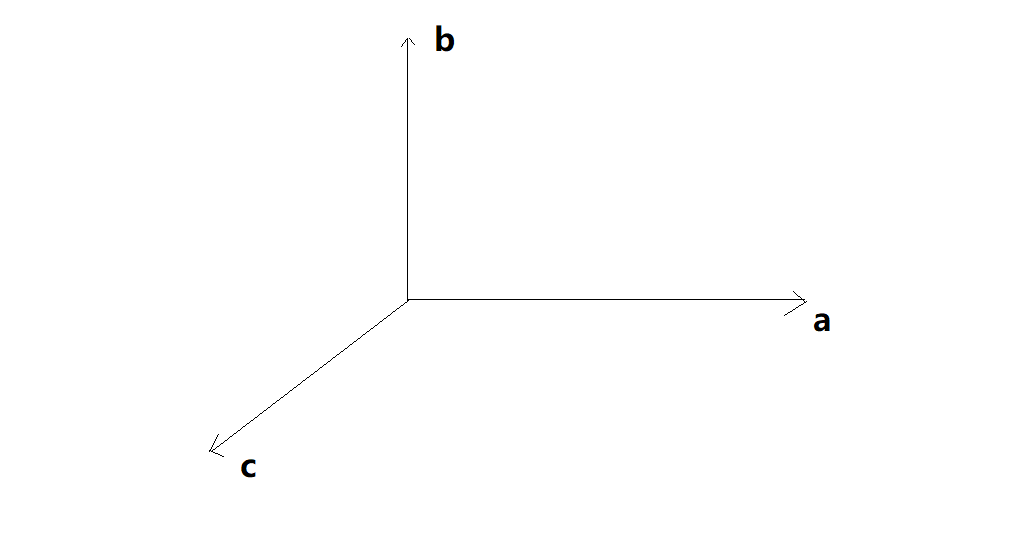
　　在游戏中，我们会用到点和向量两个点概念，点是空间中的位置，而向量具有大小和方向，在程序代码中，既可以使用类Vecctor3来表示点，也可以用来表示向量。在1.1节中，计算三角形的旋转时，初步用了向量的概念。我们使用类的模板来定义C++向量类代码如下：

 1 template <typename T>
 2 class Vector3
 3 {
 4 public:
 5     Vector3(T x, T y, T z);
 6     Vector3(T v[3]);
 7     T Length();
 8     Vector3<T> &Normalize();
 9     T DotProduct(const Vector3<T> &v) const;
10     Vector3<T> CrossProduct(const Vector3<T> &v) const;
11     Vector3<T> &RotateByX(T v);
12     Vector3<T> &RotateByY(T v);
13     Vector3<T> &RotateByZ(T v);
14     15 
16     Vector3<T> operator+(const Vector3<T> &v)const;
17     Vector3<T> operator-(const Vector3<T> &v)const;
18     Vector3<T> operator*(const Vector3<T> &v)const;
19     
20     union
21     {
22         struct
23         {
24             T x, y, z;
25         };
26         T v[3];       
27     };
28 };

上面代码定义了向量的一些基本操作，这里对坐标的定义使用了union并声明为public，以可以方便的使用x,y,z值或是通过v[1],v[2],v[3]这种下标的方式对坐标值访问，而不是增加如SetX()、GetX()这样的冗余的操作。

具体的代码定义如下：

  1 template <typename T>
  2 Vector3<T>::Vector3(T x, T y, T z)
  3 :x(x), y(y), z(z)
  4 {
  5 }
  6 
  7 template <typename T>
  8 Vector3<T>::Vector3(T v[3])
  9 {
 10     memcpy(this->v, v, sizeof(this->v));
 11 }
 12 
 13 
 14 template <typename T>
 15 T Vector3<T>::Length()
 16 {
 17     return sqrt(x * x + y * y + z * z);
 18 }
 19 
 20 template <typename T>
 21 Vector3<T> &Vector3<T>::Normalize()
 22 {
 23     T len = Length();
 24     if (len > 0)
 25     {
 26         T invLen = 1 / len;
 27         x *= invLen;
 28         y *= invLen;
 29         z *= invLen;
 30     }
 31     return *this;
 32 }
 33 
 34 template <typename T>
 35 T Vector3<T>::DotProduct(const Vector3<T> &v) const
 36 {
 37     return x * v.x + y * v.y + z * v.z;
 38 }
 39 
 40 template <typename T>
 41 Vector3<T> Vector3<T>::CrossProduct(const Vector3<T> &v) const
 42 {
 43     return Vector3<T>(
 44         y * v.z - z * v.y,
 45         z * v.x - x * v.z,
 46         x * v.y - y * v.x
 47     );
 48 }
 49 
 50 template <typename T>
 51 Vector3<T> &Vector3<T>::RotateByX(T v)
 52 {
 53     T c = static_cast<T>(cos(static_cast<long double>(v)));
 54     T s = static_cast<T>(sin(static_cast<long double>(v)));
 55     T tmpy = y * c - z * s;
 56     T tmpz = y * s + z * c;
 57     y = tmpy;
 58     z = tmpz;
 59     return *this;
 60 }
 61 
 62 template <typename T>
 63 Vector3<T> &Vector3<T>::RotateByY(T v)
 64 {
 65     T c = static_cast<T>(cos(static_cast<long double>(v)));
 66     T s = static_cast<T>(sin(static_cast<long double>(v)));
 67     T tmpx = x * c + z * s;
 68     T tmpz = -x * s + z * c;
 69     x = tmpx;
 70     z = tmpz;
 71     return *this;
 72 }
 73 
 74 template <typename T>
 75 Vector3<T> &Vector3<T>::RotateByZ(T v)
 76 {
 77     T c = static_cast<T>(cos(static_cast<long double>(v)));
 78     T s = static_cast<T>(sin(static_cast<long double>(v)));
 79     T tmpx = x * c - y * s;
 80     T tmpy = x * s + y * c;
 81     x = tmpx;
 82     y = tmpy;
 83     return *this;
 84 }
 85 
 86 template <typename T>
 87 Vector3<T> Vector3<T>::operator+(const Vector3<T> &v) const
 88 {
 89     return Vector3<T>(x + v.x, y + v.y, z + v.z);
 90 }
 91 
 92 template <typename T>
 93 Vector3<T> Vector3<T>::operator-(const Vector3<T> &v) const
 94 {
 95     return Vector3<T>(x - v.x, y - v.y, z - v.z);
 96 }
 97 
 98 template <typename T>
 99 Vector3<T> Vector3<T>::operator*(const Vector3<T> &v) const
100 {
101     return Vector3<T>(x * v.x, y * v.y, z * v.z);
102 }

 

上述代码在计算绕坐标轴旋转时，由于计算非常简单，采用了第1.1节中方式，直接使用三角函数进行计算，而并没有使用矩阵或者四元数去额外定义一个对象来处理，当然涉及到更复杂的空间变换时，则是矩阵和四元数的拿手好戏了。为了方便使用，提供如下定义来对向量和点进行定义：

1 typedef Vector3<float> Vector3f;
2 typedef Vector3f Point3f;
3 typedef Vector3<double> Vector3d;
4 typedef Vector3d Point3d;

 

posted @ 2022-06-26 17:28  毅安  阅读(228)  评论(0)  编辑  收藏  举报