Tutorial on Gabor Filters

Tutorial on Gabor Filters

1 The Temporal (1-D) Gabor Filter

Gabor filters can serve as excellent band-pass filters for unidimensionnal signals (e.g., speech)
A complex Gabor filter is defined as the product of a Gaussian kernel times a complex sinusoid, i.e.

\[g(t)=ke^{j\theta}w(at)s(t) \]

where
\(w(t)=e^{-\pi t^{2}}\)
\(s(t)=e^{j(2\pi f_{0}t)}\)
Here \(k,\theta,f_{0}\) are filter parameters. We can think of the complex Gabor filter as two out of phase filters continently allocated in the real and complex part of a complex function, the real part holds the filter

\[g_{r}(t)=w(t)sin(2\pi f_{0}t+\theta) \]

and the imaginary part holds the filter

\[g_{i}(t)=w(t)cos(2\pi f_{0}t+\theta) \]

1.1 Frequency Response

Taking the Fourier transform

\[\hat{g}(f)=ke^{j\theta}\int_{-\infty}^{\infty}e^{-j2\pi ft}w(at)s(t)dt=\frac{k}{a}e^{j\theta}\hat{w}(\frac{f-f_{0}}{a}) \]

where
\(\hat{w}(f)=w(f)=e^{-\pi f^{2}}\)

1.2 Gabor Energy Filters

The real and imaginary components of a complex Gabor filter are phase sensitive, i.e., as a consequence their response to a sinusoid is another sinusoid (Fig 1.2).
In the frequency domain, the magnitude of the response to a particular frequency is simply the magnitude of the complex Fourier transform, i.e.

\[||g(f)||=\frac{k}{a}\hat{w}(\frac{f-f_{0}}{a}) \]

Note this is a Gaussion function centered at \(f_{0}\) and with width proportional to \(\alpha\).

Fig 1. Top: An input signal. Second: Output of Gabor filter (cosine carrier). Third: Output of Gabor Filter in quadrature (sine carrier). Fourth: Output of Gabor Energy Filter.

1.2.1 Bandwidth and Peak Response

Thus the peak filter response is at \(f_{0}\). To get the half-magnitude bandwidth \(\Delta_{f}\) note

\[\hat{w}(\frac{f-f_{0}}{a})=e^{-\pi\frac{f-f_{0}}{\alpha^2}}=0.5 \]

Thus the half peak magnitude is achieved for

\[f-f_{0}\pm\sqrt{\alpha^{2}log2\pi}=0.4697\alpha\approx 0.5\alpha \]

Thus the half-magnitude bandwidth is approximately equal to \(\alpha\).

1.3 Eliminating the DC response

Depending on the value of \(f_{0}\) and \(alpha\) the filter may have a large DC response. A popular approach to get a zero DC response is to subtract the output of a low-pass Gaussian filter

\[h(t)=g(t)-cw(bt)=ke^{j\theta}w(at)s(t)-cw(bt) \]

Thus

\[\hat{h}(f)=\hat{g}(f)-\frac{c}{b}\hat{w}(\frac{f}{b}) \]

To get a zero DC response we need

\[\frac{c}{b}\hat{w}(0)=\hat{g}(0) \]

\[c=b\hat{g}(0)=b\frac{k}{a}e^{j\theta}\hat{w}(\frac{f_{0}}{\alpha}) \]

Thus

\[h(t)=ke^{j\theta}(w(\alpha t)s(t)-\frac{b}{a}\hat{w}(\frac{f_{0}}{\alpha})w(bt)) \]

\[\hat{h}(f)=\frac{k}{a}e^{j\theta}(\hat{w}(\frac{f-f_{0}}{\alpha})-\hat{w}(\frac{f_{0}}{a})\hat{w}(\frac{f}{b})) \]

It is convenient, to let \(b=a\), in which case

\[h(t)=ke^{j\theta}w(\alpha t)(s(t)-\hat{w}(\frac{f_{0}}{a}) \]

\[\hat{h}(f)=\frac{k}{a}e^{j\theta}(\hat{w}(\frac{f-f_{0}}{\alpha})-\hat{w}(\frac{f_{0}}{a})\hat{w}(\frac{f}{a})) \]

2 The Spatial (2-D) Gabor Filter

Here is the formula of a complex Gabor function in space domain

\[g(x,y)=s(x,y)w_{r}(x,y) \]

where \(s\) is a complex sinusoid, known as the carrier, and \(w_{r}\) is a 2-D Gaussian-shaped function, known as the envelope.

In the spatial domain, a 2-D Gabor filter is a Gaussian kernel function modulated by a complex sinusoidal plane wave, defined as:

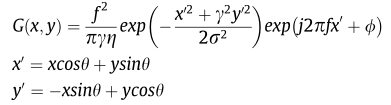
where \(f\) is the frequency of the sinusoid,
\(\theta\) represents the orientation of the normal to the paraller stripes of a Gabor function,
\(\phi\) is the phase offset,
\(\sigma\) is the standard deviation of the Gaussian envelope,
and \(\gamma\) is the spatial aspect ratio which specifies the ellipticity of the support of the Gabor function

2.1 The complex sinusoid carrier

The complex sinusoid is defined as follows

\[s(x,y)=exp(j(2\pi(u_{0}x+v_{0}y)+P)) \]

where \((u_{0},v_{0})\) and \(P\) define the spatial frequency and the phase of the sinusoid respectively.
We can think of this sinusoid as two separate real functions, conveniently allocated in the real and imaginary part of a complex function

The real part and the imaginary part of this sinusoid are

\[Re(s(x,y))=cos(2\pi(u_{0}x+v_{0}y)+P) \]

\[Im(s(x,y))=sin(2\pi(u_{0}x+v_{0}y)+P) \]

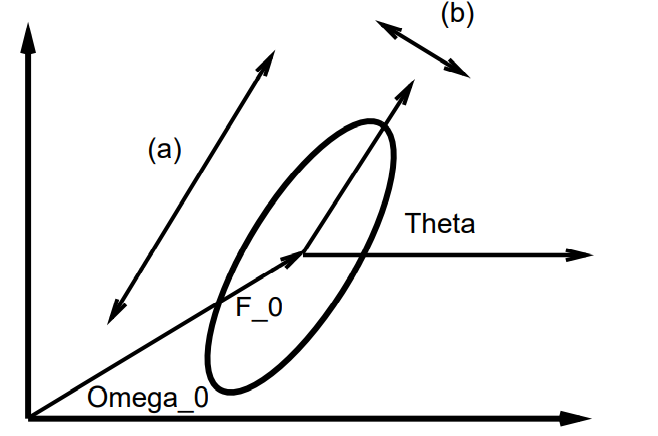
The parameters \(u_{0}\) and \(v_{0}\) define the spatial frequency of the sinusoid in Cartesian coordinates. This spatial frequency can also be expressed in polar coordinates as magnitude \(F_{0}\) and direction \(\omega_{0}\)

\[F_{0}=\sqrt{u_{0}^{2}+v_{0}^{2}} \]

\[\omega_{0}=tan^{-1}(\frac{v_{0}}{u_{0}}) \]

i.e.

\[u_{0}=F_{0}cos\omega_{0} \]

\[v_{0}=F_{0}sin\omega_{0} \]

\[s(x,y)=exp(j(2\pi F_{0}(xcos\omega_{0}+ysin\omega_{0})+P)) \]

2.2 The Gaussian envelope

The Gaussian envelope looks as follows

\[w_{r}(x,y)=Kexp(-\pi(a^2(x-x_{0})^2_{r}+b^2(y-y_{0})^2_{r})) \]

where \((x_{0},y_{0})\) is the peak of the function, \(a\) and \(b\) are scaling parameters of the Gaussian (Note that the Gaussian gets smaller in the space domain, if \(a\) and \(b\) get larger), and the \(_{r}\) subscript stands for a rotation operation (clockwise) such that

\[(x-x_{0})_{r}=(x-x_{0})cos\theta+(y-y_{0})sin\theta \]

\[(y-y_{0})_{r}=(x-x_{0})sin\theta+(y-y_{0})cos\theta \]

2.3 The complex Gabor function

The complex Gabor function is defined by the following 9 parameters

• \(K\) : Scales the magnitude of the Gaussian envelope.
• \((a,b)\) : Scale the two axis of the Gaussian envelope.
• \(\theta\) : Rotation angle of the Gaussian envelope.
• \((x_{0},y_{0})\) : Location of the peak of Gaussian envelope.
• \((u_{0},v_{0})\) : Spatial frequencies of the sinusoid carrier in Cartesian coordinates.
  It can also be expressed in polar coordinates as \((F_{0},\omega_{0})\)
• \(P\) : Phase of the sinusoid carrier.

Fig 2. A Gaussian envelope. The image is 128x128 pixels. The parameters are as follows: $x_{0}=y_{0}=0, a=1/50 pixels, b=1/40 pixels, \theta=-45 deg$.

Fig 3. The real and imaginary parts of a complex Gabor function in space domain. The image is 128x128 pixels. The parameters are as follows: $x_{0}=y_{0}=0, a=1/50 pixels, b=1/40 pixels, \theta=-45 deg$.$\omega_{0}=45 deg, P=0 deg$ .

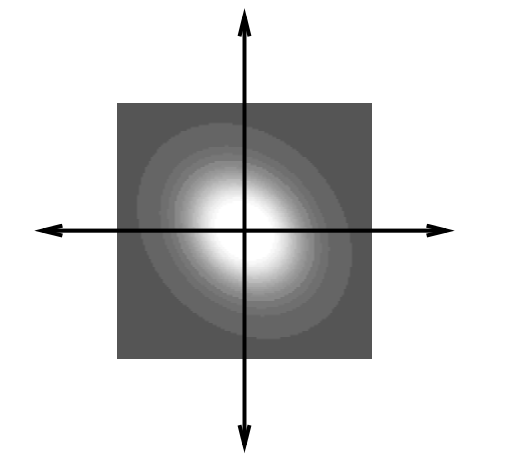
Now we have the complex Gabor function in space domain

\[g(x,y)=w_{r}(x,y)s(x,y) \]

\[w_{r}(x,y)=Kexp(-\pi(a^2(x-x_{0})^2_{r}+b^2(y-y_{0})^2_{r})) \]

\[s(x,y)=exp(j(2\pi F_{0}(xcos\omega_{0}+ysin\omega_{0})+P))=exp(j(2\pi(u_{0}x+v_{0}y)+P)) \]

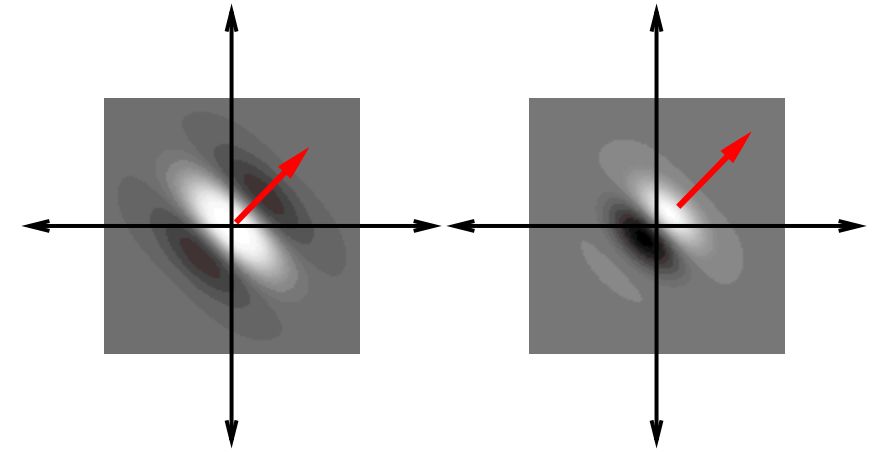
The 2-D Fourier transform of this Gabor is as follows

\[\hat{g}(u.v)=\frac{K}{ab}exp(j(-2\pi(x_{0}(u-u_{0})+y_{0}(v-v_{0}))+P))\\exp(-\pi(\frac{(u-u_{0})_{r}^2}{a^2}+\frac{(v-v_{0})_{r}^2}{b^2})) \]

Fig 4. The Fourier transform of Gabor filter. The peak response is at the spatial frequency of the complex sinusoid: $u_{p}=v_{p}=1/80cycles/pixel$. The parameters are as follows: $x_{0}=y_{0}=0, a=1/50 pixels, b=1/40 pixels, \theta=-45 deg$.$F_{0}=\sqrt{2}/80cycles/pixel,\omega_{0}=45 deg, P=0 deg$ .

3 Half-magnitude profile

We just need to find the set of points \((u,v)\) with magnitude \(K/2ab\)

\[\frac{1}{2}\frac{K}{ab}=\frac{K}{ab}exp(-\pi(\frac{(u-u_{0})_{r}^2}{a^2}+\frac{(v-v_{0})_{r}^2}{b^2})) \]

or equivalently,

\[(\frac{(u-u_{0})_{r}^2}{aC})^2+(\frac{(v-v_{0})_{r}^2}{bC})^2=1 \]

where \(C=\sqrt{\frac{log2}{\pi}}\approx 0.5\)
is an ellipse centered at \((u_{0},v_{0})\) rotated with an angle \(\theta\) with respect to the \(u\) axis. The main axis of the ellipse have length \(2aC\approx a\) and \(2bC\approx b\) respectively.

Fig 5. Parameters of the Gabor kernel as reflected in the half-magnitude elliptic profile. Note that this is a figure in frequency domain.

4 Gabor functions as models of simple cell receptive fields

Jones and Palmer (1987) showed that the real part of complex Gabor functions fit very well the receptive field weight functions found in simple cells in cat striate cortex.
Here are some useful pieces information for designing biologically inspired Gabor filters.

• To a first approx the orientation of the Gaussian envelop \(\omega_{0}\) can be modeled as being quivalent to the orientation of the carrier.\(\theta_{0}=\omega_{0}\). The actual absolute deviations between \(\theta_{0}\) and \(\omega_{0}\) have a Median of about 10 degrees.
• ...

5 Gabor functions for spatial frequency filtering

Consider a massive set of simple cell neurons with Gabor kernel functions with equal parameters except for the location parameters \((x_{0},y_{0})\). Let all these neurons be distributed uniformly about the foveal field. Each point in the foveal(中心凹) field. Each point in the foveal field contains at least two neurons in quadrature.

We can model the operation of such a set of neurons as a convolution operation (assuming a continuous and uniform distribution of filters in all the foveal locations).

Since convolution in space domain is product in frequency domain, the set of Gabor functions work as bandpass frequency filters of the foveal image.

The peak frequency is controlled by the spatial frequency of the sinusoid carrier \((u_{0}, v_{0})\). The half-magnitude region is controlled by the rotation \(\theta\) and scale parameters a, b, of the Gaussian envelope.

6 Functional Interpretations

Section in preparation:

• minimizes number of neurons needed to achieve a desired frequency resolution.
• spatially and frequency localized.
• matched to "logons" likely to occur in images.
• for natural images the Gabor representation is more sparse than the \(\delta\)(pixel) representation and than the DOG representation.