ML --Softmax Function (Multiclass Classification) --Andrew Ng ---- Optional Lab

Optional Lab - Softmax Function¶
In this lab, we will explore the softmax function. This function is used in both Softmax Regression and in Neural Networks when solving Multiclass Classification problems.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | import numpy as npimport matplotlib.pyplot as pltplt.style.use('./deeplearning.mplstyle')import tensorflow as tffrom tensorflow.keras.models import Sequentialfrom tensorflow.keras.layers import Densefrom IPython.display import display, Markdown, Latexfrom sklearn.datasets import make_blobs%matplotlib widgetfrom matplotlib.widgets import Sliderfrom lab_utils_common import dlcfrom lab_utils_softmax import plt_softmaximport logginglogging.getLogger("tensorflow").setLevel(logging.ERROR)tf.autograph.set_verbosity(0) |
Note: Normally, in this course, the notebooks use the convention of starting counts with 0 and ending with N-1,
while lectures start with 1 and end with N,
This is because code will typically start iteration with 0 while in lecture, counting 1 to N leads to cleaner, more succinct equations. This notebook has more equations than is typical for a lab and thus will break with the convention and will count 1 to N.
Softmax Function¶
In both softmax regression and neural networks with Softmax outputs, N outputs are generated and one output is selected as the predicted category. In both cases a vector z is generated by a linear function which is applied to a softmax function. The softmax function converts z into a probability distribution as described below. After applying softmax, each output will be between 0 and 1 and the outputs will add to 1, so that they can be interpreted as probabilities. The larger inputs will correspond to larger output probabilities.
The softmax function can be written:

The output a is a vector of length N, so for softmax regression, you could also write:

Which shows the output is a vector of probabilities. The first entry is the probability the input is the first category given the input x and parameters w and b.
Let's create a NumPy implementation:
1 2 3 4 | def my_softmax(z): ez = np.exp(z) #element-wise exponenial sm = ez/np.sum(ez) return(sm) |
Below, vary the values of the z inputs using the sliders.
1 2 | plt.close("all")plt_softmax(my_softmax) |
As you are varying the values of the z's above, there are a few things to note:
- the exponential in the numerator of the softmax magnifies small differences in the values
- the output values sum to one
- the softmax spans all of the outputs. A change in
z0for example will change the values ofa0-a3. Compare this to other activations such as ReLu or Sigmoid which have a single input and single output.
Cost¶
The loss function associated with Softmax, the cross-entropy loss, is:

Where y is the target category for this example and a is the output of a softmax function. In particular, the values in a are probabilities that sum to one.
Recall: In this course, Loss is for one example while Cost covers all examples.
Note in (3) above, only the line that corresponds to the target contributes to the loss, other lines are zero. To write the cost equation we need an 'indicator function' that will be 1 when the index matches the target and zero otherwise.

Now the cost is:

Where m is the number of examples, N is the number of outputs. This is the average of all the losses.
Tensorflow¶
This lab will discuss two ways of implementing the softmax, cross-entropy loss in Tensorflow, the 'obvious' method and the 'preferred' method. The former is the most straightforward while the latter is more numerically stable.
Let's start by creating a dataset to train a multiclass classification model.
1 2 3 | # make dataset for examplecenters = [[-5, 2], [-2, -2], [1, 2], [5, -2]]X_train, y_train = make_blobs(n_samples=2000, centers=centers, cluster_std=1.0,random_state=30) |
The Obvious organization¶
The model below is implemented with the softmax as an activation in the final Dense layer. The loss function is separately specified in the compile directive.
The loss function SparseCategoricalCrossentropy. The loss described in (3) above. In this model, the softmax takes place in the last layer. The loss function takes in the softmax output which is a vector of probabilities.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | model = Sequential( [ Dense(25, activation = 'relu'), Dense(15, activation = 'relu'), Dense(4, activation = 'softmax') # < softmax activation here ])model.compile( loss=tf.keras.losses.SparseCategoricalCrossentropy(), optimizer=tf.keras.optimizers.Adam(0.001), # Adam algorithm can auto find best learning rate)model.fit( X_train,y_train, epochs=10) |
Because the softmax is integrated into the output layer, the output is a vector of probabilities.
1 2 3 | p_nonpreferred = model.predict(X_train)print(p_nonpreferred [:2])print("largest value", np.max(p_nonpreferred), "smallest value", np.min(p_nonpreferred)) |
Preferred
Recall from lecture, more stable and accurate results can be obtained if the softmax and loss are combined during training. This is enabled by the 'preferred' organization shown here.
In the preferred organization the final layer has a linear activation. For historical reasons, the outputs in this form are referred to as logits. The loss function has an additional argument: from_logits = True. This informs the loss function that the softmax operation should be included in the loss calculation. This allows for an optimized implementation.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | preferred_model = Sequential( [ Dense(25, activation = 'relu'), Dense(15, activation = 'relu'), Dense(4, activation = 'linear') #<-- Note ])preferred_model.compile( loss=tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True), #<-- Note optimizer=tf.keras.optimizers.Adam(0.001), # Adam algorithm can auto find best learning rate, it is more faste; rate=0.001) preferred_model.fit( X_train,y_train, epochs=10 ) |
Output Handling¶
Notice that in the preferred model, the outputs are not probabilities, but can range from large negative numbers to large positive numbers. The output must be sent through a softmax when performing a prediction that expects a probability. Let's look at the preferred model outputs:
1 2 3 | p_preferred = preferred_model.predict(X_train)print(f"two example output vectors:\n{p_preferred[:2]}")print("largest value", np.max(p_preferred), "smallest value", np.min(p_preferred)) |
The output predictions are not probabilities! If the desired output are probabilities, the output should be be processed by a softmax.
1 2 3 | sm_preferred = tf.nn.softmax(p_preferred).numpy()print(f"two example output vectors:\n{sm_preferred[:2]}")print("largest value", np.max(sm_preferred), "smallest value", np.min(sm_preferred)) |
To select the most likely category, the softmax is not required. One can find the index of the largest output using np.argmax().
1 2 | for i in range(5): print( f"{p_preferred[i]}, category: {np.argmax(p_preferred[i])}") |
SparseCategorialCrossentropy or CategoricalCrossEntropy¶
Tensorflow has two potential formats for target values and the selection of the loss defines which is expected.
- SparseCategorialCrossentropy: expects the target to be an integer corresponding to the index. For example, if there are 10 potential target values, y would be between 0 and 9.
- CategoricalCrossEntropy: Expects the target value of an example to be one-hot encoded where the value at the target index is 1 while the other N-1 entries are zero. An example with 10 potential target values, where the target is 2 would be [0,0,1,0,0,0,0,0,0,0].
Numerical Stability (optional)¶
This section discusses some of the methods employed to improve numerical stability. This is for the interested reader and is not at all required.
Softmax Numerical Stability¶
The input's to the softmax are the outputs of a linear layer 
. These may be large numbers. The first step of the softmax algorithm computes ezj. This can result in an overflow error if the number gets too large. Try running the cell below:
1 2 3 4 | for z in [500,600,700,800]: ez = np.exp(z) zs = "{" + f"{z}" + "}" print(f"e^{zs} = {ez:0.2e}") |
The operation will generate an overflow if the exponent gets too large. Naturally, my_softmax() will generate the same errors:
1 2 | z_tmp = np.array([[500,600,700,800]])my_softmax(z_tmp) |
Numerical stability can be improved by reducing the size of the exponent. Recall

if the b were the opposite sign of a, this would reduce the size of the exponent. Specifically, if you multiplied the softmax by a fraction:

the exponent would be reduced and the value of the softmax would not change. If b in eb were the largest value of the zj's, maxj(z), the exponent would be reduced to its smallest value.

It is customary to say  since the equation would be correct with any constant C.
since the equation would be correct with any constant C.
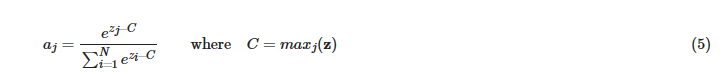
If we look at our troublesome example where z contains 500,600,700,800, 

Let's rewrite my_softmax to improve its numerical stability.
1 2 3 4 5 6 | def my_softmax_ns(z):"""numerically stablility improved""" bigz = np.max(z) ez = np.exp(z-bigz) # minimize exponent sm = ez/np.sum(ez) return(sm) |
Let's try this and compare it to the tensorflow implementation:
1 2 | z_tmp = np.array([500.,600,700,800])print(tf.nn.softmax(z_tmp).numpy(), "\n", my_softmax_ns(z_tmp)) |
Large values no longer cause an overflow.
Cross Entropy Loss Numerical Stability¶
The loss function associated with Softmax, the cross-entropy loss, is repeated here:

Where y is the target category for this example and a is the output of a softmax function. In particular, the values in a are probabilities that sum to one. Let's consider a case where the target is two (y=2) and just look at the loss for that case. This will result in the loss being:
Recall that a2 is the output of the softmax function described above, so this can be written:

Starting from (6) above, the loss for the case of y=2:  so (6) can be rewritten:
so (6) can be rewritten:

The first term can be simplified to just z2:

It turns out that the l term in the above equation is so often used, many libraries have an implementation. In Tensorflow this is tf.math.reduce_logsumexp(). An issue with this sum is that the exponent in the sum could overflow if zi is large. To fix this, we might like to subtract emaxj(z) as we did above, but this will require a bit of work:
term in the above equation is so often used, many libraries have an implementation. In Tensorflow this is tf.math.reduce_logsumexp(). An issue with this sum is that the exponent in the sum could overflow if zi is large. To fix this, we might like to subtract emaxj(z) as we did above, but this will require a bit of work:

Now, the exponential is less likely to overflow. It is customary to say  since the equation would be correct with any constant C. We can now write the loss equation:
since the equation would be correct with any constant C. We can now write the loss equation:
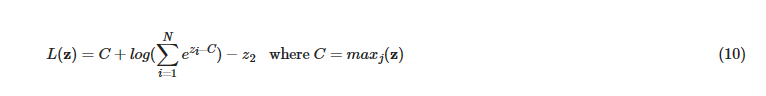
A computationally simpler, more stable version of the loss. The above is for an example where the target, y=2 but generalizes to any target.




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 【.NET】调用本地 Deepseek 模型
· CSnakes vs Python.NET:高效嵌入与灵活互通的跨语言方案对比
· Plotly.NET 一个为 .NET 打造的强大开源交互式图表库
· DeepSeek “源神”启动!「GitHub 热点速览」
· 上周热点回顾(2.17-2.23)