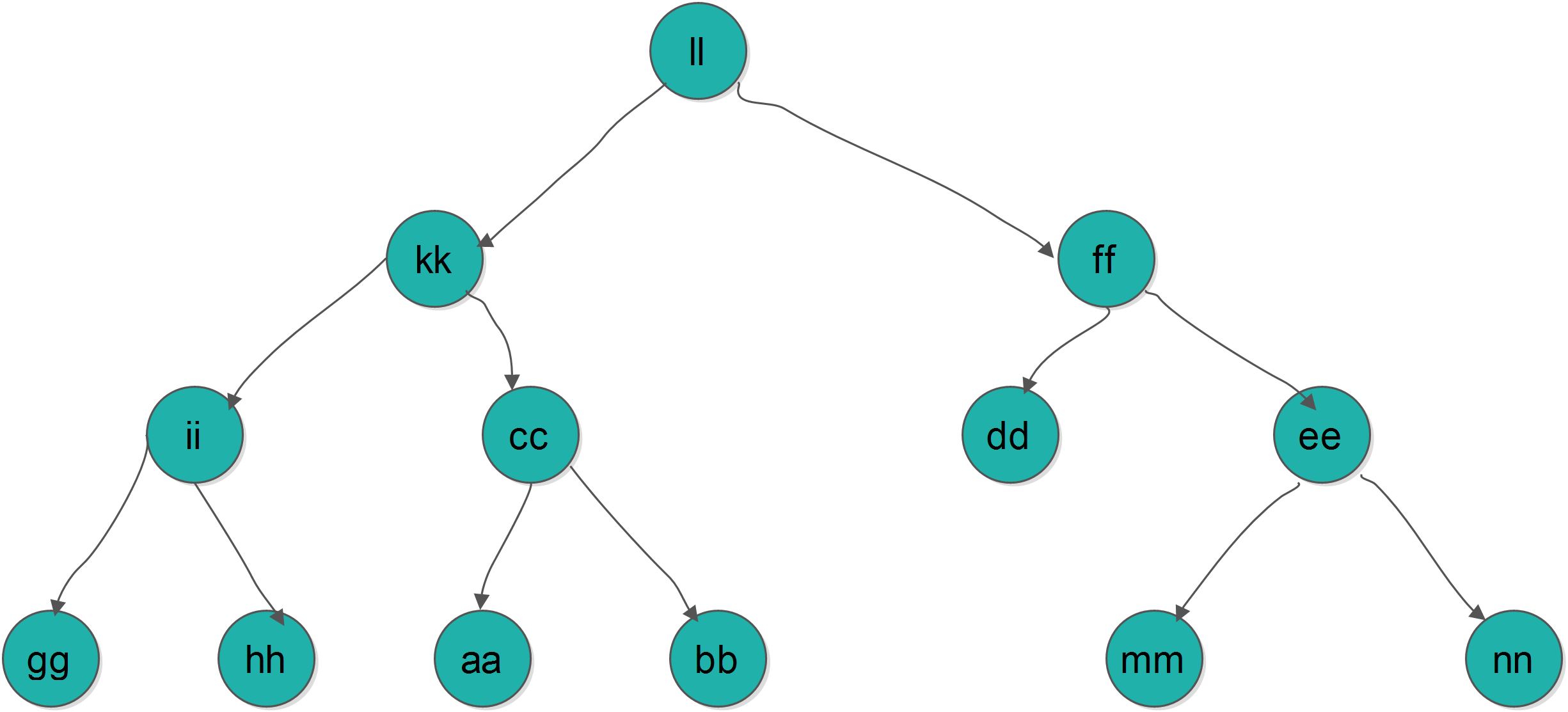
二叉树(Java链式实现)

二叉树的结构和链表很相似，都有一个“结点”的定义，在这个结点之中，则是“二叉”的体现，和单链表的next的作用一样，都是指向下一个节点，也++可以理解为Cpp之中的leftTree,*rgihtTree的作用++，都是一个指向的作用，在此处，内部的节点类，使用static修饰，这样方便结点的创建，在每个结点之中，====有数据域，leftchild和right child三个变量。====在创建二叉树的时候，此处提供了两种方式，一种是通过结点的累积，通过节点之间的left，right的关系，将结点先联结起来，然后将其结点的组合赋值给二叉树对象，这样，只需要创建一个二叉树的对象，第二种方式是++通过二叉树的递归特性，使用子树来创建一个二叉树，基本的思路是首先将所有的结点全设成一个只有一个结点的二叉树，然后再通过节点和二叉树子树，来完成一个二叉树的赋值++，这样做的时候有两个问题需要注意，一个是这样会新建很多二叉树对象，第二点是需要在二叉树节点和二叉树子树的转换之中特别留意，二者因为是相近的概念，但是又不是同一个概念，所以在类型上是不一致的，所以，此处选择获得二叉树子树的root结点的方式，然后将三个结点进行左右孩子级别上的联结，在get_root方法之中有所体现*，另一个方面就是关于null的问题，此处设计的二叉树都是要么有左右孩子，要么就没有，只有这两种个情况，因此可能在只有一个左孩子结点或者右孩子结点的情况下出现问题，这点需要主意，以后有时间补上。

另外就是关于二叉树的遍历，遍历的话此处实现了先（前）序遍历，中序遍历和后序遍历三种情况，暂时还未实现层次遍历，没有实现获取节点总数的方法和获取二叉树深度（高度）的方法，以后补上。

public class TTree
{
    //树的节点
    static class Node
    {
        private String data;
        Node left_child;
        Node right_child;

        Node(String data)
        {
            this.data = data;
            this.left_child = null;
            this.right_child = null;
        }
    }

    //根节点
    public Node root;
    public int height;
    public int length;

    /**
     * 通过节点，来组成一棵树
     */
    public TTree() { }

    public TTree(Node node)
    {
        this.root = node;
    }

    public TTree(Node node, TTree left_tree, TTree right_tree)
    {
        this.root = node;
        root.left_child = get_root(left_tree);
        root.right_child = get_root(right_tree);
    }


    /**
     * 通过节点，来组成一棵树
     */

    public void set_left_child(Node parent, Node left)
    {
        parent.left_child = left;
        parent.left_child = left;
    }

    public void set_right_child(Node parent, Node right)
    {
        parent.right_child = right;
    }

    public void set_two_child(Node parent, Node left, Node right)
    {
        parent.left_child = left;
        parent.right_child = right;
    }

    /**
     * 通过子树，来组成一棵树
     */
    /*创造一个单个节点的树*/
    public void set_tree(Node node)
    {
        this.root = node;//结点和树之间的转换是一个关键
    }

    /*通过子树来完成树木的创建*/
    public void set_tree(Node node, TTree left_tree, TTree right_tree)
    {
        set_tree_transfer(node, left_tree, right_tree);
    }

    /*完成子树和子树节点之间的转化，主要是通过取得子树的根节点，将根节点转化为目标节点的左右孩子*/
    private void set_tree_transfer(Node node, TTree left_tree, TTree right_tree)
    {
        node.left_child = left_tree.get_root(left_tree);
        node.right_child = right_tree.get_root(right_tree);
    }

    /*取得树的根节点*/
    public Node get_root(TTree tree)
    {
        Node node = null;
        if (tree.root != null)
        {
            node = tree.root;
            return node;
        } else return null;

    }

    /*获得二叉树的树高*/
    public int get_height(TTree tt)
    {
        return 0;
    }

    /*获得总的节点数目*/
    public int get_node_number()
    {
        return 0;
    }

    /**
     * 遍历
     */
    //先序遍历
    public void preorder_traversal(Node cur)
    {
        if (cur != null) System.out.print(cur.data + ",");
        if (cur.left_child != null) preorder_traversal(cur.left_child);
        if (cur.right_child != null) preorder_traversal(cur.right_child);
    }

    //中序遍历
    public void inorder_traversal(Node cur)
    {
        if (cur.left_child != null) inorder_traversal(cur.left_child);
        if (cur != null) System.out.print(cur.data + ",");
        if (cur.right_child != null) inorder_traversal(cur.right_child);
    }

    //后序遍历
    public void postorder_traversal(Node cur)
    {
        if (cur.left_child != null) postorder_traversal(cur.left_child);
        if (cur.right_child != null) postorder_traversal(cur.right_child);
        if (cur != null) System.out.print(cur.data + ",");
    }


    public static void main(String[] args)
    {
        System.out.println("结点构造...");
        //结点
        Node a = new Node("A");
        Node b = new Node("B");
        Node c = new Node("C");
        Node d = new Node("D");
        Node e = new Node("E");
        Node f = new Node("F");
        //二叉树
        TTree t = new TTree();
        t.root = a;
        t.set_two_child(t.root, b, c);
        t.set_right_child(b, d);
        t.set_left_child(c, e);
        t.set_right_child(c, f);
        Node cur = t.root;
        t.preorder_traversal(cur);//前序遍历
        System.out.println("");
        t.inorder_traversal(cur);//中序遍历
        System.out.println("");
        t.postorder_traversal(cur);//后序遍历
        System.out.println("");


        System.out.println("子树构造...");
        //结点
        Node aa = new Node("a");
        Node bb = new Node("b");
        Node cc = new Node("c");
        Node dd = new Node("d");
        Node ee = new Node("e");
        Node ff = new Node("f");
        Node gg = new Node("g");
        Node hh = new Node("h");
        Node ii = new Node("i");
        Node jj = new Node("j");
        Node kk = new Node("k");
        Node ll = new Node("l");
        Node mm = new Node("m");
        Node nn = new Node("n");

        //子树
        TTree tta = new TTree(aa);
        TTree ttb = new TTree(bb);
        TTree ttd = new TTree(dd);
        TTree tte = new TTree(ee);
        TTree ttm = new TTree(mm);
        TTree ttn = new TTree(nn);
        TTree ttg = new TTree(gg);
        TTree tth = new TTree(hh);
        TTree tc = new TTree(cc, tta, ttb);
        TTree tf = new TTree(ff, ttd, tte);
        TTree te = new TTree(ee, ttm, ttn);
        TTree ti = new TTree(ii, ttg, tth);
        TTree tk = new TTree(kk, ti, tc);
        TTree tl = new TTree(ll, tk, tf);
        tl.inorder_traversal(tl.root);
    }
}