CoAtNet: 90.88% Paperwithcode榜单第一，层层深入考虑模型设计

【GiantPandaCV导语】CoAt=Convolution + Attention，paperwithcode榜单第一名，通过结合卷积与Transformer实现性能上的突破，方法部分设计非常规整，层层深入考虑模型的架构设计。

引言

Transformer模型的容量大，由于缺乏正确的归纳偏置，泛化能力要比卷积网络差。

提出了CoAtNets模型族：

• 深度可分离卷积与self-attention能够通过简单的相对注意力来统一化。
• 叠加卷积层和注意层在提高泛化能力和效率方面具有惊人的效果

方法

这部分主要关注如何将conv与transformer以一种最优的方式结合：

• 在基础的计算块中，如果合并卷积与自注意力操作。
• 如何组织不同的计算模块来构建整个网络。

合并卷积与自注意力

卷积方面谷歌使用的是经典的MBConv， 使用深度可分离卷积来捕获空间之间的交互。

卷积操作的表示：\(\mathcal{L}(i)\)代表i周边的位置，也即卷积处理的感受野。

\[y_{i}=\sum_{j \in \mathcal{L}(i)} w_{i-j} \odot x_{j} \quad \text { (depthwise convolution) } \]

自注意力表示：\(\mathcal{G}\)表示全局空间感受野。

\[y_{i}=\sum_{j \in \mathcal{G}} \underbrace{\frac{\exp \left(x_{i}^{\top} x_{j}\right)}{\sum_{k \in \mathcal{G}} \exp \left(x_{i}^{\top} x_{k}\right)}}_{A_{i, j}} x_{j} \quad \text { (self-attention) } \]

融合方法一：先求和，再softmax

\[y_{i}^{\text {post }}=\sum_{j \in \mathcal{G}}\left(\frac{\exp \left(x_{i}^{\top} x_{j}\right)}{\sum_{k \in \mathcal{G}} \exp \left(x_{i}^{\top} x_{k}\right)}+w_{i-j}\right) x_{j} \]

融合方法二：先softmax，再求和

\[y_{i}^{\text {pre }}=\sum_{j \in \mathcal{G}} \frac{\exp \left(x_{i}^{\top} x_{j}+w_{i-j}\right)}{\sum_{k \in \mathcal{G}} \exp \left(x_{i}^{\top} x_{k}+w_{i-k}\right)} x_{j} \]

出于参数量、计算两方面的考虑，论文打算采用第二种融合方法。

垂直布局设计

决定好合并卷积与注意力的方式后应该考虑如何构建网络整体架构，主要有三个方面的考量：

• 使用降采样降低空间维度大小，然后使用global relative attention。
• 使用局部注意力，强制全局感受野限制在一定范围内。典型代表有：
  • Scaling local self-attention for parameter efficient visual backbone
  • Swin Transformer
• 使用某种线性注意力方法来取代二次的softmax attention。典型代表有：
  • Efficient Attention
  • Transformers are rnns
  • Rethinking attention with performers

第二种方法实现效率不够高，第三种方法性能不够好，因此采用第一种方法，如何设计降采样的方式也有几种方案：

• 使用卷积配合stride进行降采样。
• 使用pooling操作完成降采样，构建multi-stage网络范式。
• 根据第一种方案提出\(ViT_{REL}\), 即使用ViT Stem，直接堆叠L层Transformer block使用relative attention。
• 根据第二种方案，采用multi-stage方案提出模型组：\(S_0,...,S_4\),如下图所示：

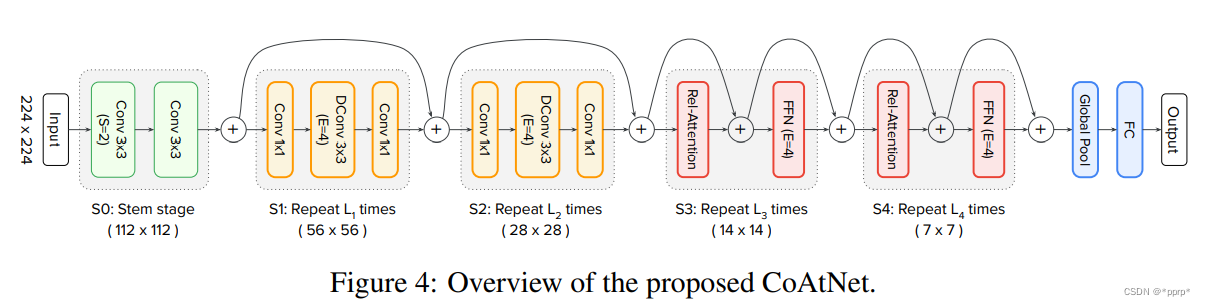
\(S_o-S_2\)采用卷积以及MBConv，从\(S_2-S_4\)的几个模块采用Transformer 结构。具体Transformer内部有以下几个变体：C代表卷积，T代表Transformer

• C-C-C-C
• C-C-C-T
• C-C-T-T
• C-T-T-T

初步测试模型泛化能力

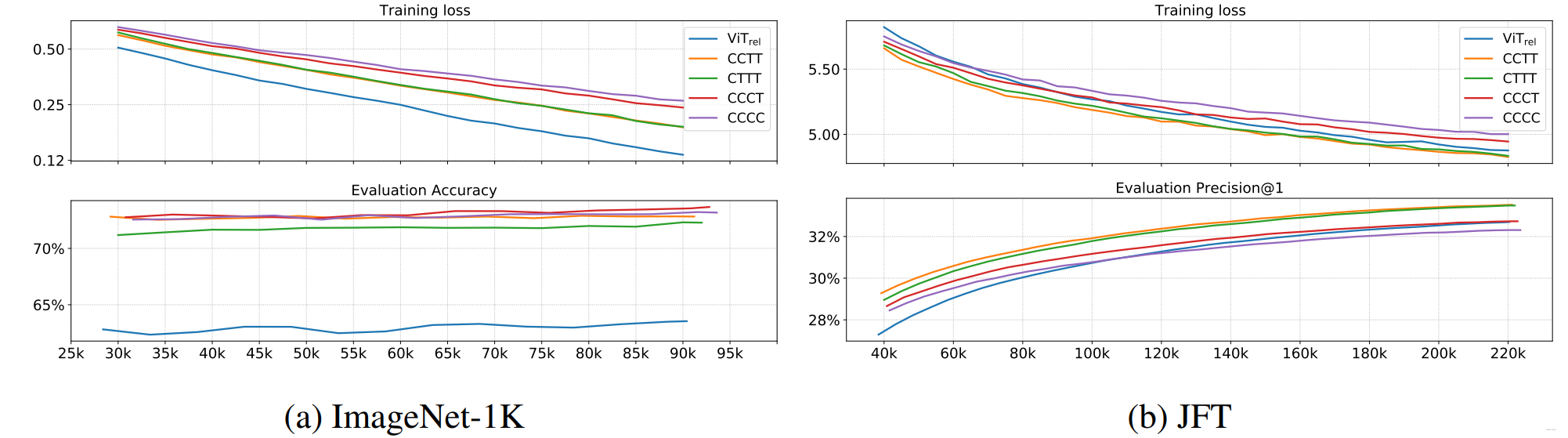
泛化能力排序为：（证明架构中还是需要存在想当比例的卷积操作）

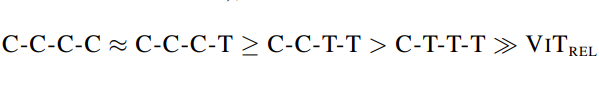
初步测试模型容量

主要是从JFT以及ImageNet-1k上不同的表现来判定的，排序结果为：

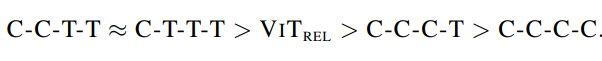
测试模型迁移能力

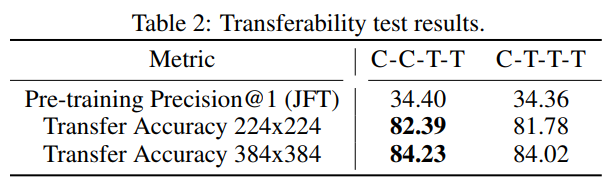
为了进一步比较CCTT与CTTT，进行了迁移能力测试，发现CCTT能够超越CTTT。

最终CCTT胜出！

实验

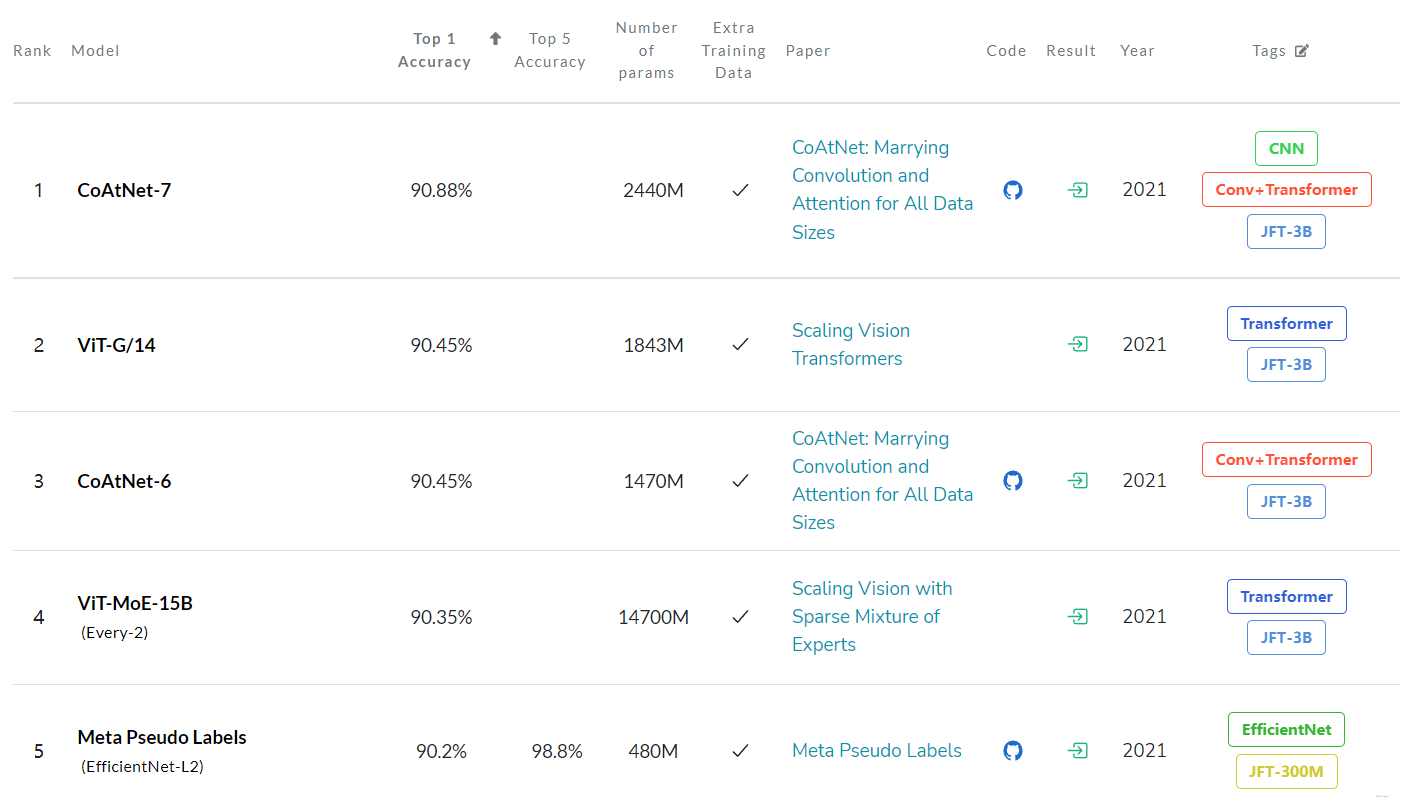
与SOTA模型比较结果：

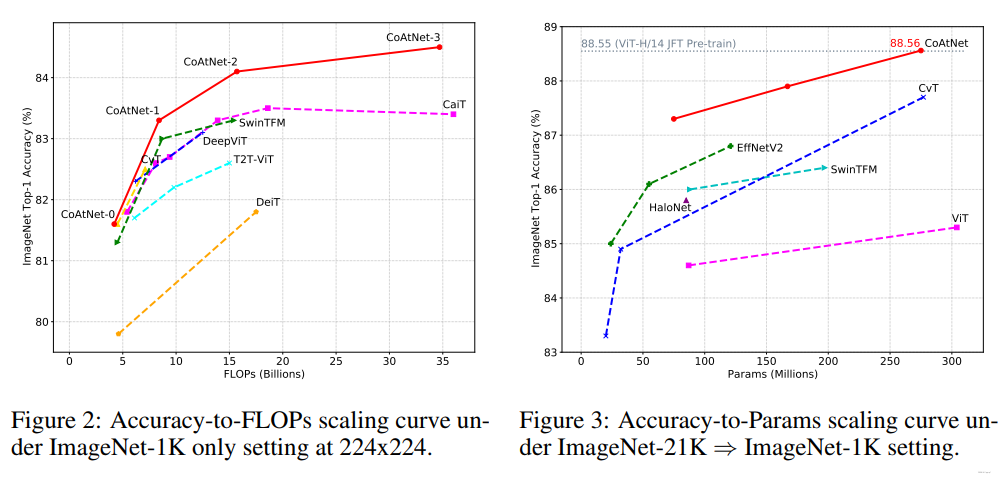
实验结果：

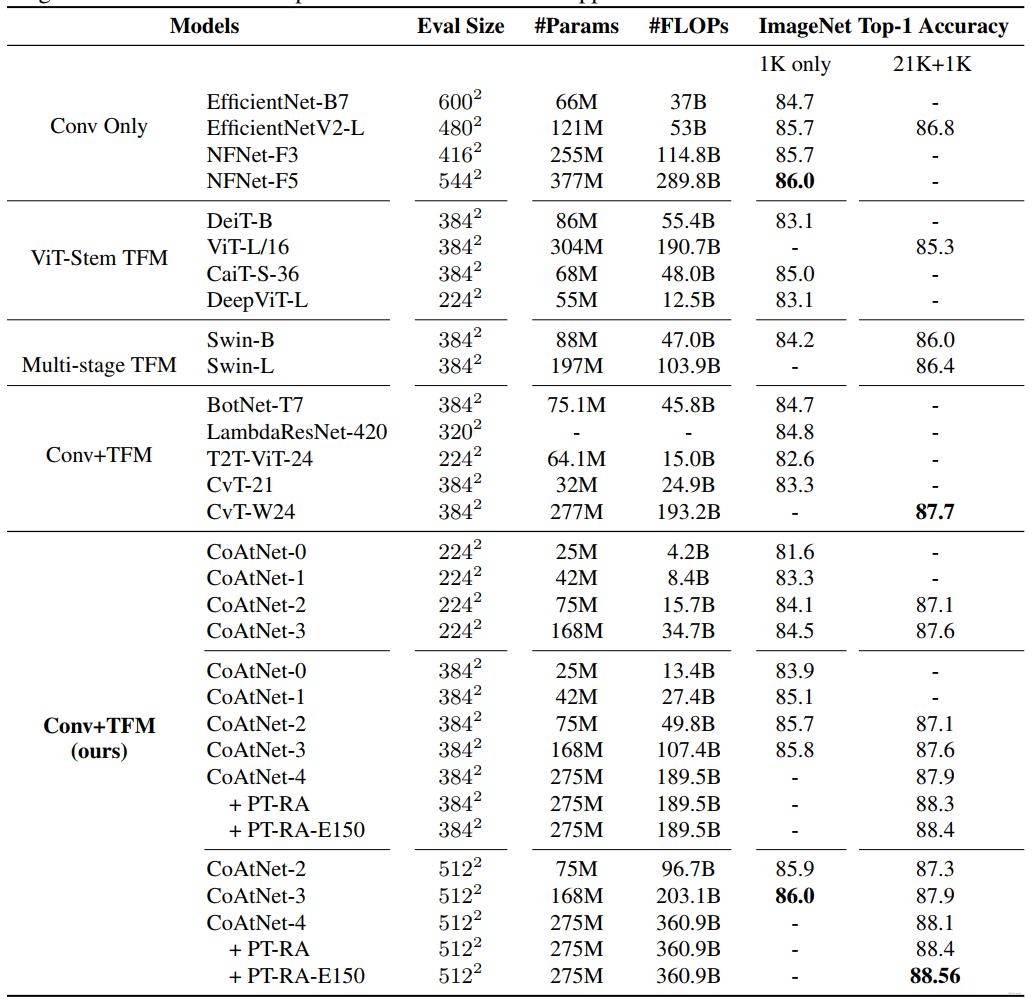
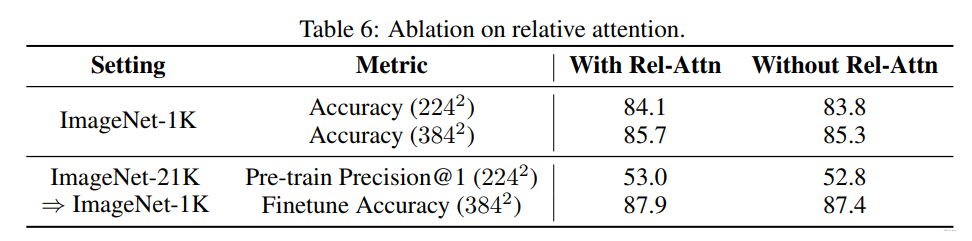
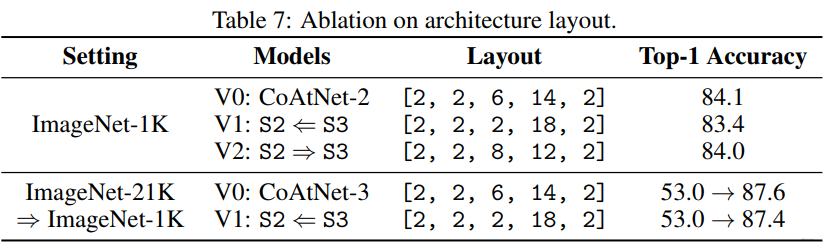
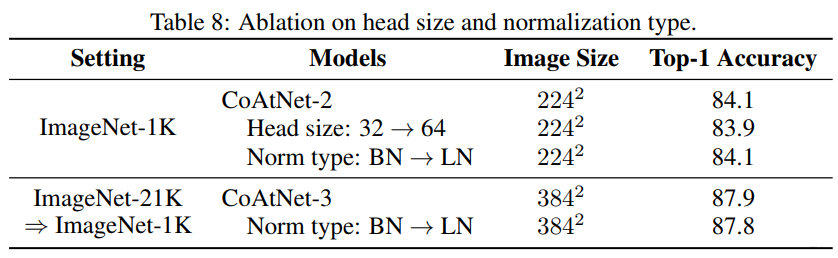
消融实验：

代码

浅层使用的MBConv模块如下：

class MBConv(nn.Module):
    def __init__(self, inp, oup, image_size, downsample=False, expansion=4):
        super().__init__()
        self.downsample = downsample
        stride = 1 if self.downsample == False else 2
        hidden_dim = int(inp * expansion)

        if self.downsample:
            self.pool = nn.MaxPool2d(3, 2, 1)
            self.proj = nn.Conv2d(inp, oup, 1, 1, 0, bias=False)

        if expansion == 1:
            self.conv = nn.Sequential(
                # dw
                nn.Conv2d(hidden_dim, hidden_dim, 3, stride,
                          1, groups=hidden_dim, bias=False),
                nn.BatchNorm2d(hidden_dim),
                nn.GELU(),
                # pw-linear
                nn.Conv2d(hidden_dim, oup, 1, 1, 0, bias=False),
                nn.BatchNorm2d(oup),
            )
        else:
            self.conv = nn.Sequential(
                # pw
                # down-sample in the first conv
                nn.Conv2d(inp, hidden_dim, 1, stride, 0, bias=False),
                nn.BatchNorm2d(hidden_dim),
                nn.GELU(),
                # dw
                nn.Conv2d(hidden_dim, hidden_dim, 3, 1, 1,
                          groups=hidden_dim, bias=False),
                nn.BatchNorm2d(hidden_dim),
                nn.GELU(),
                SE(inp, hidden_dim),
                # pw-linear
                nn.Conv2d(hidden_dim, oup, 1, 1, 0, bias=False),
                nn.BatchNorm2d(oup),
            )
        
        self.conv = PreNorm(inp, self.conv, nn.BatchNorm2d)

    def forward(self, x):
        if self.downsample:
            return self.proj(self.pool(x)) + self.conv(x)
        else:
            return x + self.conv(x)

主要关注Attention Block设计，引入Relative Position:

class Attention(nn.Module):
    def __init__(self, inp, oup, image_size, heads=8, dim_head=32, dropout=0.):
        super().__init__()
        inner_dim = dim_head * heads
        project_out = not (heads == 1 and dim_head == inp)

        self.ih, self.iw = image_size

        self.heads = heads
        self.scale = dim_head ** -0.5

        # parameter table of relative position bias
        self.relative_bias_table = nn.Parameter(
            torch.zeros((2 * self.ih - 1) * (2 * self.iw - 1), heads))

        coords = torch.meshgrid((torch.arange(self.ih), torch.arange(self.iw)))
        coords = torch.flatten(torch.stack(coords), 1)
        relative_coords = coords[:, :, None] - coords[:, None, :]

        relative_coords[0] += self.ih - 1
        relative_coords[1] += self.iw - 1
        relative_coords[0] *= 2 * self.iw - 1
        relative_coords = rearrange(relative_coords, 'c h w -> h w c')
        relative_index = relative_coords.sum(-1).flatten().unsqueeze(1)
        self.register_buffer("relative_index", relative_index)

        self.attend = nn.Softmax(dim=-1)
        self.to_qkv = nn.Linear(inp, inner_dim * 3, bias=False)

        self.to_out = nn.Sequential(
            nn.Linear(inner_dim, oup),
            nn.Dropout(dropout)
        ) if project_out else nn.Identity()

    def forward(self, x):
        qkv = self.to_qkv(x).chunk(3, dim=-1)
        q, k, v = map(lambda t: rearrange(
            t, 'b n (h d) -> b h n d', h=self.heads), qkv)

        dots = torch.matmul(q, k.transpose(-1, -2)) * self.scale

        # Use "gather" for more efficiency on GPUs
        relative_bias = self.relative_bias_table.gather(
            0, self.relative_index.repeat(1, self.heads))
        relative_bias = rearrange(
            relative_bias, '(h w) c -> 1 c h w', h=self.ih*self.iw, w=self.ih*self.iw)
        dots = dots + relative_bias

        attn = self.attend(dots)
        out = torch.matmul(attn, v)
        out = rearrange(out, 'b h n d -> b n (h d)')
        out = self.to_out(out)
        return out

参考

https://arxiv.org/pdf/2106.04803.pdf

https://github.com/chinhsuanwu/coatnet-pytorch