机器学习 —— 逻辑回归

机器学习 —— 逻辑回归原理

模型介绍

Logistic Regression 虽然被称为回归，但其实际上是分类模型，并常用于二分类。Logistic Regression 因其简单、可并行化、可解释强深受工业界喜爱

Logistic 回归的本质是：假设数据服从这个分布，然后使用极大似然估计做参数的估计

Logistic 分布

Logistic 分布是一种连续型的概率分布，其分布函数和密度函数分别为：

\[ F(x) = P(X \leq x) = \frac{1}{1+e^{\frac{-(x - \mu)}{\gamma}}}\\ f(x) = F'(X \leq x) = \frac{e^{\frac{-(x - \mu)}{\gamma}}}{\gamma (1+e^{\frac{-(x - \mu)}{\gamma}})^2} \]

其中，\(\mu\) 表示位置参数，\(\gamma > 0\) 为形状参数。我们可以看下其图像特征

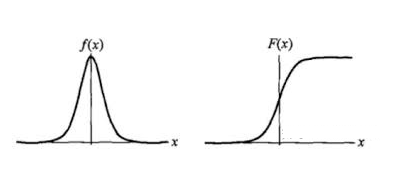
Logistic 分布是由其位置和尺度参数定义的连续分布。Logistic 分布的形状与正态分布的形状相似，但是 Logistic 分布的尾部更长，所以我们可以使用 Logistic 分布来建模比正态分布具有更长尾部和更高波峰的数据分布。在深度学习中常用到的 Sigmoid 函数就是 Logistic 的分布函数在 \(\mu = 0 , \gamma = 1\) 的特殊形式

Logistic 回归

这里以二分类为例，对于所给数据集假设存在这样的一条直线可以将数据完成线性可分

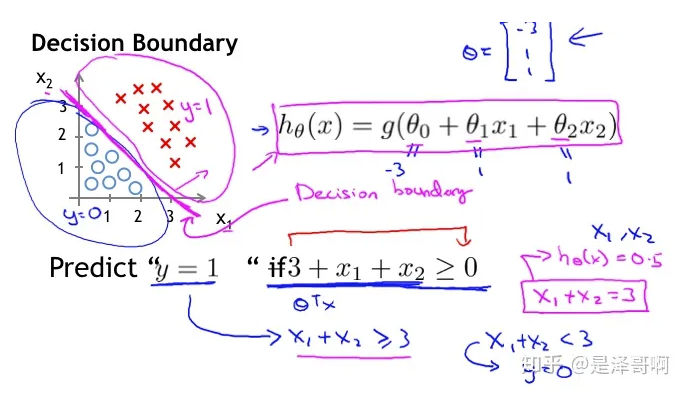
决策边界可以表示为 \(w_1x_1 + w_2x_2 + b = 0\) ，假设某个样本点，\(h_w(x) = w_1x_1 + w_2x_2 + b > 0\) 那么可以判断它的类别为 1，这个过程其实是感知机

Logistic 回归还需要加一层，它要找到分类概率 P(Y=1) 与输入向量 x 的直接关系，然后通过比较概率值来判断类别

考虑二分类问题，给定数据集

\[D = (x_1,y_1),……,(x_N,y_N),\ x_i \subseteq R^n,\ y_i \in 0,1,\ i = 1,2,……,N \]

考虑到 \(w^Tx + b\) 取值是连续的，因此它不能拟合离散变量。可以考虑用它来拟合条件概率 \(p(Y=1|x)\)，因为概率的取值也是连续的

但是对于 \(w \neq 0\) （若等于零向量则没有什么求解的价值），\(w^Tx + b\) 取值为 R，不符合概率取值为 0 到 1，因此考虑采用广义线性模型

最理想的是单位阶跃函数：

\[p(y = 1|x) = \begin{cases} 0 & z < 0 \\ 0.5 & z = 0 \\ 1 & z > 0\end{cases}\\ z = w^Tx + b \]

但是这个阶跃函数不可微，对数几率函数是一个常用的替代函数：

\[y = \frac{1}{1+e^{-(w^Tx + b)}} \]

于是：

\[ln\frac{y}{1-y} = w^tx + b \]

我们将 y 视为 x 为正例的概率，则 1-y 为 x 为其反例的概率。两者的比值称为几率（odds），指该事件发生与不发生的概率比值，若事件发生的概率为 p。则对数几率：

\[ln(odds) = ln\frac{y}{1-y} \]

将 y 视为类后验概率估计，重写公式有：

\[w^tx + b = ln\frac{P(Y = 1|x)}{1-P(Y = 1|x)}\\ P(Y = 1|x) = \frac{1}{1+e^{-w^Tx + b}} \]

也就是说，输出 Y=1 的对数几率是由输入 x 的线性函数表示的模型，这就是逻辑回归模型。当 \(w^T + b\) 的值越接近正无穷，\(P(Y = 1|x)\) 概率值也就越接近 1。因此逻辑回归的思路是，先拟合决策边界(不局限于线性，还可以是多项式)，再建立这个边界与分类的概率联系，从而得到了二分类情况下的概率

在这我们思考个问题，我们使用对数几率的意义在哪？通过上述推导我们可以看到 Logistic 回归实际上是使用线性回归模型的预测值逼近分类任务真实标记的对数几率，其优点有：

1. 直接对分类的概率建模，无需实现假设数据分布，从而避免了假设分布不准确带来的问题（区别于生成式模型）；

2. 不仅可预测出类别，还能得到该预测的概率，这对一些利用概率辅助决策的任务很有用；

3. 对数几率函数是任意阶可导的凸函数，有许多数值优化算法都可以求出最优解。

代价函数

逻辑回归模型的数学形式确定后，剩下就是如何去求解模型中的参数。在统计学中，常常使用极大似然估计法来求解，即找到一组参数，使得在这组参数下，我们的数据的似然度（概率）最大，设：

\[P(Y = 1|x) = p(x)\\ P(Y = 0|x) = 1-p(x) \]

似然函数：

\[L(w) = \prod[p(x_i)]^{y_i}[1-p(x_i)]^{1-y_i} \]

为了更方便求解，我们对等式两边同取对数，写成对数似然函数：

\[\begin{matrix} L(w) = & \sum[y_ilnp(x_i) + (1 - y_i)ln(1-p(x_i))]\\ & =\sum[y_iln\frac{p(x_i)}{1-p(x_i)} + ln(1-p(x_i))]\\ & =\sum[y_i(w \cdot x_i) - ln(1+e^{w \cdot x_i})] \end{matrix} \]

在机器学习中我们有损失函数的概念，其衡量的是模型预测错误的程度。如果取整个数据集上的平均对数似然损失，我们可以得到:

\[J(w) = -\frac{1}{N}lnL(w) \]

即在逻辑回归模型中，我们最大化似然函数和最小化损失函数实际上是等价的

求解

求解逻辑回归的方法有非常多，我们这里主要聊下梯度下降和牛顿法。优化的主要目标是找到一个方向，参数朝这个方向移动之后使得损失函数的值能够减小，这个方向往往由一阶偏导或者二阶偏导各种组合求得。逻辑回归的损失函数是：

\[J(w) = -\frac{1}{n}(\sum^n_{i=1}(y_i(lnp(x_i) + (1 - y_i)ln(1 - p(x_i)))) \]

1. 随机梯度下降

梯度下降是通过 J(w) 对 w 的一阶导数来找下降方向，并且以迭代的方式来更新参数，更新方式为:

\[g_i = \frac{\partial J(w)}{\partial w_i} = (p(x_i) - y_i)x_i\\ w_i^{k+1} = w^k_i - \alpha g_i \]

其中 k 为迭代次数。每次更新参数后，可以通过比较 \(||J(w^{k + 1}) - J(w^k)||\) 小于阈值或者到达最大迭代次数来停止迭代

2. 牛顿法

牛顿法的基本思路是，在现有极小点估计值的附近对 f(x) 做二阶泰勒展开，进而找到极小点的下一个估计值。假设 \(w^k\) 为当前的极小值估计值，那么有：

\[\varphi(w) = J(w^k) + J'(w^k)(w - w^k) + \frac{1}{2}J''(w^k)(w - w^k)^2 \]

然后令 \(\varphi(w) = 0\)，得到了 \(w^{k + 1} = w^k - \frac{J'(w^k)}{J''(w^k)}\),因此有迭代更新式：

\[w^{k + 1} = w^k - \frac{J'(w^k)}{J''(w^k)} = w^k - H^{-1}_k \cdot g_k \]

其中 \(H^{-1}_k\) 为海森矩阵：

\[H_{mn} = \frac{\partial^2J(w)}{\partial w_m\partial w_n} = h(x^i)(1 - p_w(x^i))x^i_mx^i_n \]

此外，这个方法需要目标函数是二阶连续可微的，本文中的 \(J(w)\) 是符合要求的。

介绍

在本练习中，您将实现逻辑回归并将其应用于两个不同的数据集。还将通过将正则化加入训练算法，来提高算法的鲁棒性，并用更复杂的情形来测试模型算法。

在开始练习前，需要下载如下的文件进行数据上传：

• ex2data1.txt -前半部分的训练数据集
• ex2data2.txt -后半部分的训练数据集

在整个练习中，涉及如下的必做作业：

• 绘制2D分类数据的函数----(3分)
• 实现Sigmoid函数--------(5分)
• 实现Logistic回归代价函数和梯度函数---(60分)
• 实现回归预测函数--------(5分)
• 实现正则Logisitic回归成本函数-------(27分)

1 Logistic回归

在该部分练习中，将建立一个逻辑回归模型，用以预测学生能否被大学录取。

假设你是大学某个部门的负责人，你要根据两次考试的结果来决定每个申请人的入学机会。目前已经有了以往申请者的历史数据，并且可以用作逻辑回归的训练集。对于每行数据，都包含对应申请者的两次考试分数和最终的录取结果。

在本次练习中，你需要建立一个分类模型，根据这两次的考试分数来预测申请者的录取结果。

1.1 数据可视化

在开始实施任何算法模型之前，最好先对数据进行可视化，这将会更加直观的获取数据特征。

现在，你需要编写代码来完成数据的绘图，显示如下所示的图形。

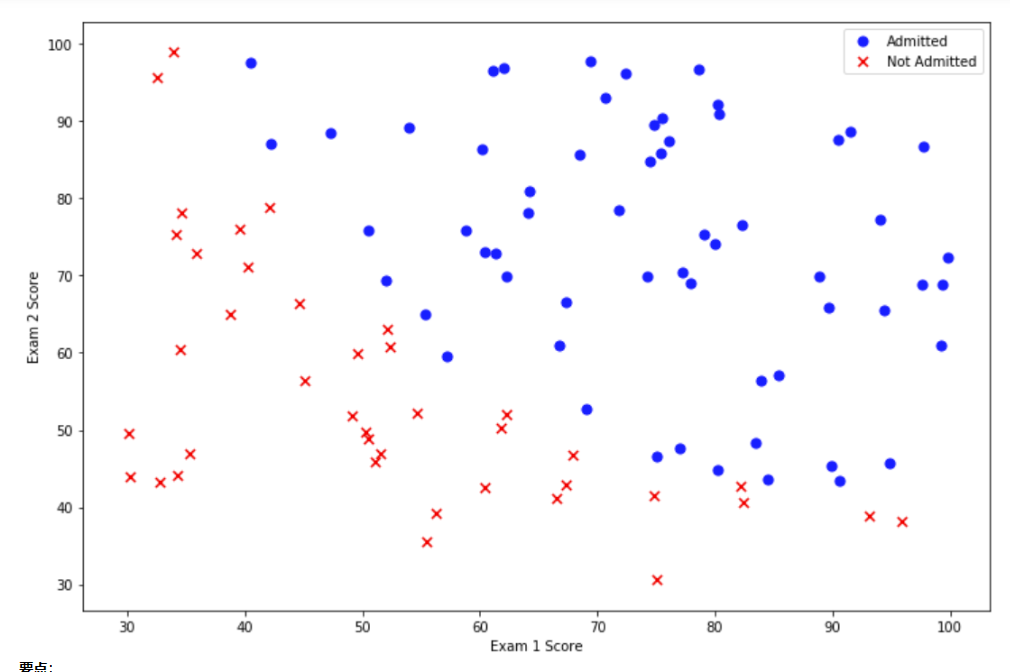
要点：

• 导入需要使用的python库，并将从文件ex2data1.txt中读取数据，并显示前5行
• x-y轴分别为两次考试的分数
• 正负示例需要用不同的标记显示（不同的颜色）

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# import matplotlib.pyplot as plt_plot
path = '/home/jovyan/work/ex2data1.txt'
data = pd.read_csv(path, header=None, names=['Exam 1', 'Exam 2', 'Admitted'])
data.head()

	Exam 1	Exam 2	Admitted
0	34.623660	78.024693	0
1	30.286711	43.894998	0
2	35.847409	72.902198	0
3	60.182599	86.308552	1
4	79.032736	75.344376	1

positive = data[data['Admitted'].isin([1])]
negative = data[data['Admitted'].isin([0])]
fig, ax = plt.subplots(figsize=(12,8))
# 正向类，绘制50个样本，c=‘b’颜色，maker=‘o’绘制的形状
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=50, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=50, c='r', marker='x', label='Not Admitted')
ax.legend()# Legend 图例,获取label标签内容，如图右上角显示
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')

Text(0, 0.5, 'Exam 2 Score')

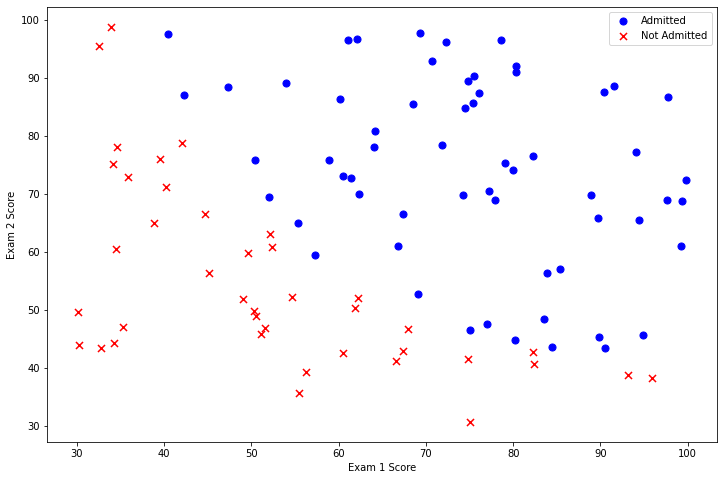
1.2 实现

在前部分练习中所绘制的数据分布图中可以看出，在不同标识的数据点间，有一个较为清晰的决策边界。现在需要实现逻辑回归，并使用逻辑回归来训练模型用以预测分类结果。

1.2.1 Sigmoid函数

在正式开始之前，我们先来了解一个函数：Sigmoid函数。
我们还记得逻辑回归假设的定义是：

\[{{h}_{\theta }}\left( x \right)=g\left({{{\theta }^{T}}X} \right)\]

其中 g 代表一个常用的逻辑函数为S形函数（Sigmoid function），公式为：
\[g\left( z \right)=\frac{1}{1+{{e}^{-z}}}\]
合起来，我们得到逻辑回归模型的假设函数：
\[{{h}_{\theta }}\left( x \right)=\frac{1}{1+{{e}^{-{{\theta }^{T}}X}}}\]

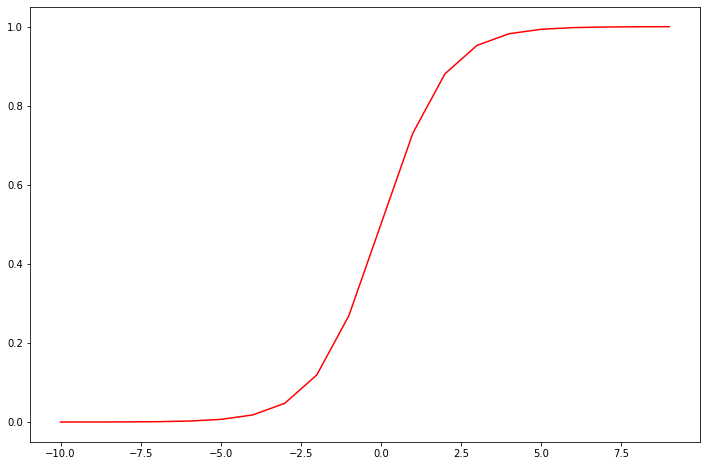
接下来，你需要编写代码实现Sigmoid函数，编写后试着测试一些值，如果x的正值较大，则函数值应接近1；如果x的负值较大，则函数值应接近0。而对于x等于0时，则函数值为0.5。

确保在进行调用你实现的Sigmoid函数后，以下代码会输出如下的图片：

def sigmoid(z):
    return 1.0/(1.0+np.exp(-z)) 

###请运行并测试你的代码###
nums = np.arange(-10, 10, step=1)

fig, ax = plt.subplots(figsize=(12,8))
ax.plot(nums, sigmoid(nums), 'r')
plt.show()

1.2.2 代价函数和梯度

1.2.2.1 代价函数

我们知道逻辑回归的代价函数是：
\(J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{{y}^{(i)}}\log \left( {{h}_{\theta }}\left( {{x}^{(i)}} \right) \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1-{{h}_{\theta }}\left( {{x}^{(i)}} \right) \right)]}\)

现在，你需要编写代码实现代价函数以进行逻辑回归的成本计算，并且经过所给数据测试后，初始的成本约为0.693。

要点：

• 实现cost函数，参数为theta，X，y.
• 返回计算的成本值。
• 其中theta为参数，X为训练集中的特征列，y为训练集的标签列，三者均为矩阵。

def cost(theta,X,y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X* theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X* theta.T)))
    return np.sum(first - second) / (len(X))

###请运行并测试你的代码###
#增加一列值为1，这和我们在练习1中的操作很相似
data.insert(0,'Ones',1)

# 定义X为训练数据，y为目的变量
cols = data.shape[1]
X = data.iloc[:,0:cols-1]
y = data.iloc[:,cols-1:cols]

# 将X,y转换为numpy数组，并初始化theta值为0
X = np.array(X.values)
y = np.array(y.values)
theta = np.zeros(3)

cost(theta, X, y)

0.6931471805599453

1.2.2.2 梯度下降

接下来，我们需要编写代码实现梯度下降用来计算我们的训练数据、标签和一些参数\(\theta\)的梯度。

要点：

• 代码实现gradient函数，参数为theta，X，y.
• 返回计算的梯度值。
• 其中theta为参数，X为训练集中的特征列，y为训练集的标签列，三者均为矩阵。

批量梯度下降转化为向量化计算： \(\frac{1}{m} X^T( Sigmoid(X\theta) - y )\)

\[\frac{\partial J\left( \theta \right)}{\partial {{\theta }_{j}}}=\frac{1}{m}\sum\limits_{i=1}^{m}{({{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}})x_{_{j}}^{(i)}} \]

这里需要注意的是，我们实际上没有在这个函数中执行梯度下降，我们仅仅在计算一个梯度步长。由于我们使用Python，我们可以用SciPy的optimize命名空间来做同样的事情。

###在这里填入代码###
def gradient(theta, X, y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)
    
    error = sigmoid(X * theta.T) - y
    
    for i in range(parameters):
        term = np.multiply(error, X[:,i])
        grad[i] = np.sum(term) / len(X)
    
    return grad

###请运行并测试你的代码###
gradient(theta, X, y)

array([ -0.1       , -12.00921659, -11.26284221])

1.2.3 寻找最优参数

现在可以用SciPy's truncated newton（TNC）实现寻找最优参数。

###请运行并测试你的代码###
import scipy.optimize as opt
result = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, y))
result

(array([-25.16131868,   0.20623159,   0.20147149]), 36, 0)

让我们看看在这个结论下代价函数的值：

###请运行并测试你的代码###
cost(result[0], X, y)

0.2034977015894744

1.2.4 评估逻辑回归

接下来，我们需要编写代码实现预测函数，用所学的最优参数\(\theta\)来为数据集X输出预测结果。然后，可以使用这个函数来给我们定义的分类器的训练精度进行打分。

逻辑回归的假设函数：

\[{{h}_{\theta }}\left( x \right)=\frac{1}{1+{{e}^{-{{\theta }^{T}}X}}}\]
当\({{h}_{\theta }}\)大于等于0.5时，预测 y=1

当\({{h}_{\theta }}\)小于0.5时，预测 y=0。

要点：

• 代码实现predict函数，参数为theta，X.
• 返回X中的每行数据对应的预测结果。
• 其中theta为参数，X为训练集中的特征列。

###在这里填入代码###
def predict(theta, X):
    probability = sigmoid(X * theta.T)
    return [1 if x >= 0.5 else 0 for x in probability]

###请运行并测试你的代码###
theta_min = np.matrix(result[0])
predict(theta_min, X)

[0,
 0,
 0,
 1,
 1,
 0,
 1,
 0,
 1,
 1,
 1,
 0,
 1,
 1,
 0,
 1,
 0,
 0,
 1,
 1,
 0,
 1,
 0,
 0,
 1,
 1,
 1,
 1,
 0,
 0,
 1,
 1,
 0,
 0,
 0,
 0,
 1,
 1,
 0,
 0,
 1,
 0,
 1,
 1,
 0,
 0,
 1,
 1,
 1,
 1,
 1,
 1,
 1,
 0,
 0,
 0,
 1,
 1,
 1,
 1,
 1,
 0,
 0,
 0,
 0,
 0,
 1,
 0,
 1,
 1,
 0,
 1,
 1,
 1,
 1,
 1,
 1,
 1,
 0,
 1,
 1,
 1,
 1,
 0,
 1,
 1,
 0,
 1,
 1,
 0,
 1,
 1,
 0,
 1,
 1,
 1,
 1,
 1,
 0,
 1]

###请运行并测试你的代码###
predictions = predict(theta_min, X)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
accuracy = (sum(map(int, correct)) % len(correct))
print ('accuracy = {0}%'.format(accuracy))

accuracy = 89%

2 正则化逻辑回归

在本部分练习中，我们将要通过加入正则项提升逻辑回归算法。

正则化是成本函数中的一个术语，它使算法更倾向于“更简单”的模型。这个理论助于减少过拟合，提高模型的泛化能力。

设想你是工厂的生产主管，你有一些芯片在两次测试中的测试结果。对于这两次测试，你想决定芯片是要被接受或抛弃。为了帮助你做出艰难的决定，你拥有过去芯片的测试数据集，从其中你可以构建一个逻辑回归模型。

2.1 数据可视化

与第一部分的练习类似，首先对数据进行可视化：

path =  '/home/jovyan/work/ex2data2.txt'
data2 = pd.read_csv(path, header=None, names=['Test 1', 'Test 2', 'Accepted'])
data2.head()

	Test 1	Test 2	Accepted
0	0.051267	0.69956	1
1	-0.092742	0.68494	1
2	-0.213710	0.69225	1
3	-0.375000	0.50219	1
4	-0.513250	0.46564	1

positive = data2[data2['Accepted'].isin([1])]
negative = data2[data2['Accepted'].isin([0])]

fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(positive['Test 1'], positive['Test 2'], s=50, c='b', marker='o', label='Accepted')
ax.scatter(negative['Test 1'], negative['Test 2'], s=50, c='r', marker='x', label='Rejected')
ax.legend()
ax.set_xlabel('Test 1 Score')
ax.set_ylabel('Test 2 Score')
plt.show()

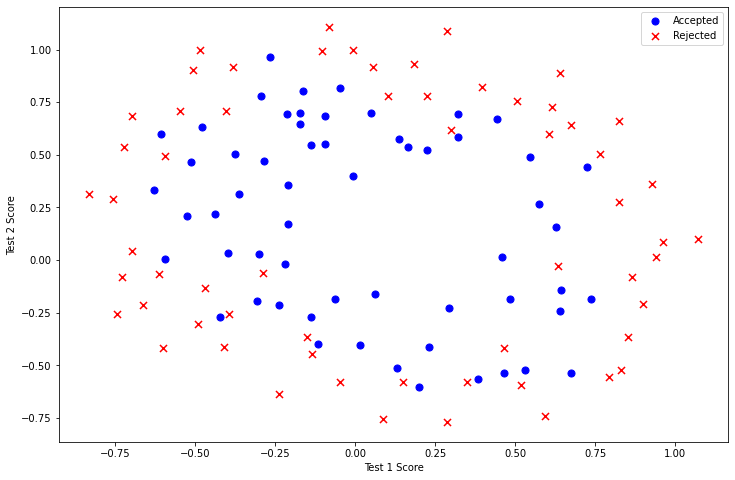
对于这部分数据，我们可以看出不同类别的数据点之间没有明显的线性决策界限用于划分两类数据。

因此，逻辑回归无法在此数据集上得到较好的效果，因为逻辑回归只能知道线性决策边界。

2.2 特征映射

一种能够更好地拟合数据的方法是构造从原始特征的多项式中得到的特征，即特征映射。如下图所示，作为这种映射的结果，我们的两个特征向量\(x_1,x_2\)（两次质量保证测试的分数）已经被转换成了28维的向量。

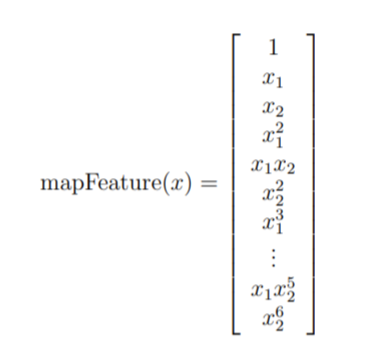
在这个高维特征向量上训练的逻辑回归分类器将具有更复杂的决策边界，并在二维图中绘制时呈现非线性的划分曲线。

虽然特征映射允许我们构建一个更具有表现力的分类器，但它也更容易过拟合。接下来，你需要实现正则化逻辑回归用于拟合数据，并使用正则化来帮助解决过拟合问题。

我们通过创建一组多项式特征来开始！

# 设定映射深度
degree = 5
# 分别取两次测试的分数
x1 = data2['Test 1']
x2 = data2['Test 2']

data2.insert(3, 'Ones', 1)

# 设定计算方式进行映射
for i in range(1, degree):
    for j in range(0, i):
        data2['F' + str(i) + str(j)] = np.power(x1, i-j) * np.power(x2, j)

# 整理数据列
data2.drop('Test 1', axis=1, inplace=True)
data2.drop('Test 2', axis=1, inplace=True)

print("特征映射后具有特征维数：%d" %data2.shape[1])
data2.head()

特征映射后具有特征维数：12

	Accepted	Ones	F10	F20	F21	F30	F31	F32	F40	F41	F42	F43
0	1	1	0.051267	0.002628	0.035864	0.000135	0.001839	0.025089	0.000007	0.000094	0.001286	0.017551
1	1	1	-0.092742	0.008601	-0.063523	-0.000798	0.005891	-0.043509	0.000074	-0.000546	0.004035	-0.029801
2	1	1	-0.213710	0.045672	-0.147941	-0.009761	0.031616	-0.102412	0.002086	-0.006757	0.021886	-0.070895
3	1	1	-0.375000	0.140625	-0.188321	-0.052734	0.070620	-0.094573	0.019775	-0.026483	0.035465	-0.047494
4	1	1	-0.513250	0.263426	-0.238990	-0.135203	0.122661	-0.111283	0.069393	-0.062956	0.057116	-0.051818

2.3 代价函数和梯度

接下来，你需要编写代码来实现计算正则化逻辑回归的代价函数和梯度，并返回计算的代价值和梯度。

正则化逻辑回归的代价函数如下：

\[J\left( \theta \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{[-{{y}^{(i)}}\log \left( {{h}_{\theta }}\left( {{x}^{(i)}} \right) \right)-\left( 1-{{y}^{(i)}} \right)\log \left( 1-{{h}_{\theta }}\left( {{x}^{(i)}} \right) \right)]}+\frac{\lambda }{2m}\sum\limits_{j=1}^{n}{\theta _{j}^{2}}\ \]

其中\(\lambda\)是“学习率”参数，其值会影响函数中的正则项值。且不应该正则化参数\(\theta_0\)。

###在这里填入代码###
def costReg(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
    reg = (learningRate / (2 * len(X))) * np.sum(np.power(theta[:,1:theta.shape[1]], 2))
    return np.sum(first - second) / len(X) + reg

接下来，我们需要实现正则化梯度函数，使用梯度下降法使得代价函数最小化。

因为在代价函数的计算中我们未对\(\theta_0\)进行正则化，所以梯度下降算法将分为两种情况：

\[\begin{align} & Repeat\text{ }until\text{ }convergence\text{ }\!\!\{\!\!\text{ } \\ & \text{ }{{\theta }_{0}}:={{\theta }_{0}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{[{{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}}]x_{_{0}}^{(i)}} \\ & \text{ }{{\theta }_{j}}:={{\theta }_{j}}-a\frac{1}{m}\sum\limits_{i=1}^{m}{[{{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}}]x_{j}^{(i)}}+\frac{\lambda }{m}{{\theta }_{j}} \\ & \text{ }\!\!\}\!\!\text{ } \\ & Repeat \\ \end{align} \]

对上面的算法中 j=1,2,...,n 时的更新式子进行调整可得：
\({{\theta }_{j}}:={{\theta }_{j}}(1-a\frac{\lambda }{m})-a\frac{1}{m}\sum\limits_{i=1}^{m}{({{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}})x_{j}^{(i)}}\)

def gradientReg(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)
    
    error = sigmoid(X * theta.T) - y
    
    for i in range(parameters):
        term = np.multiply(error, X[:,i])
        
        if (i == 0):
            grad[i] = np.sum(term) / len(X)
        else:
            grad[i] = (np.sum(term) / len(X)) + ((learningRate / len(X)) * theta[:,i])
    
    return grad

接下来，类似于第一部分的练习中，进行变量的初始化。

# 从数据集中取得对应的特征列和标签列
cols = data2.shape[1]
X2 = data2.iloc[:,1:cols]
y2 = data2.iloc[:,0:1]

# 转换为Numpy数组并初始化theta为零矩阵
X2 = np.array(X2.values)
y2 = np.array(y2.values)
theta2 = np.zeros(11)

# 设置初始学习率为1，后续可以修改
learningRate = 1

接下来，使用初始化的变量值来测试你实现的代价函数和梯度函数。

###请运行并测试你的代码###
costReg(theta2, X2, y2, learningRate)

0.6931471805599454

###请运行并测试你的代码###
gradientReg(theta2, X2, y2, learningRate)

array([0.00847458, 0.01878809, 0.05034464, 0.01150133, 0.01835599,
       0.00732393, 0.00819244, 0.03934862, 0.00223924, 0.01286005,
       0.00309594])

2.4 寻找最优参数

现在我们可以使用和第一部分相同的优化函数来计算优化后的结果。

result2 = opt.fmin_tnc(func=costReg, x0=theta2, fprime=gradientReg, args=(X2, y2, learningRate))
result2

(array([ 0.53010246,  0.29075567, -1.60725764, -0.58213819,  0.01781027,
        -0.21329507, -0.40024142, -1.3714414 ,  0.02264304, -0.95033581,
         0.0344085 ]), 22, 1)

2.5 评估正则化逻辑回归

最后，我们可以使用第1部分中的预测函数来查看我们的方案在训练数据上的准确度。

theta_min = np.matrix(result2[0])
predictions = predict(theta_min, X2)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y2)]
accuracy = (sum(map(int, correct)) % len(correct))
print ('accuracy = {0}%'.format(accuracy))

accuracy = 78%