信号的基本概念和分类

信号的基本概念和分类

通信系统

为传送消息而装设的全套设备技术

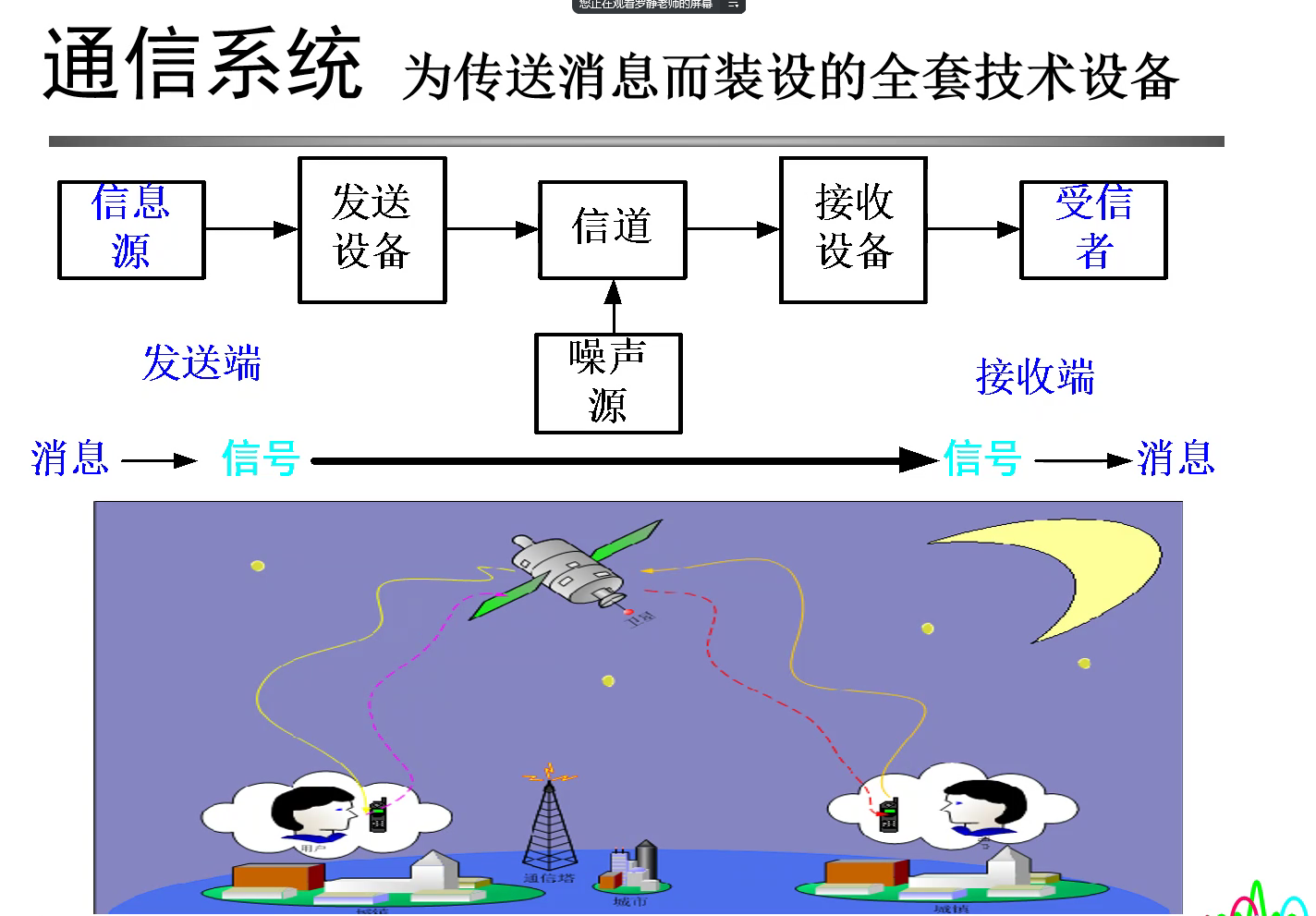
接收设备就是发送设备的逆过程，发送设备有编码器，接收设备肯定就有译码器

信号的描述和分类

信号的描述

信号是信息的一种物理体现，他一般是随时间或位置变化的物理量

信号按物理属性分：电信号和非电信号。他们可以相互转换。

电信号容易产生，便于控制，易于处理。本课程讨论电信号——简称“信号”

电信号的基本形式：随时间变化的电压或电流

描述信号的方法：
（1）表示为时间的函数
（2）信号的图形表示——波形图

信号的分类

按实际用途划分：

电视信号、雷达信号、控制信号、通信信号、广播信号、……

按所具有的时间特性划分：

确定信号和随机信号、连续信号和离散信号、周期信号和非周期信号、能量信号与功率信号、一维信号和多维信号、因果信号和反因果信号、实信号和复信号、左边信号和右边信号等

确定信号和随机信号

确定性信号：可用确定的时间函数表示的信号，对于指定的某一时刻\(t\)，有确定的函数值\(f(t)\)

随机信号：值具有不确定性的信号，如电子系统中的起伏热噪声、雷电干扰信号

伪随机信号：貌似随机而遵循严格规律产生的信号（伪随机码）

连续信号和离散信号

连续时间信号：在连续的时间范围内\((-\infty<t<-\infty)\)有定义的信号，简称连续信号

波形如下图所示：

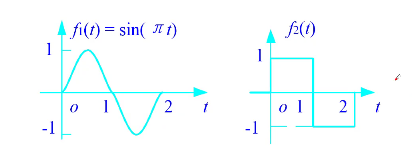
这里的“连续”指函数的定义域——时间是连续的，但可含间断点，至于至于可连续也可不连续
用\(t\)表示时间变量

离散时间信号：尽在一些离散的瞬间才有定义的信号，简称离散信号

波形图如下：

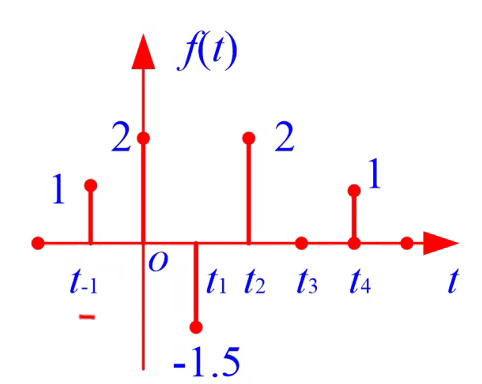
定义域——时间是离散的，他只在某些规定的离散瞬间给函数值，其余时间无定义（无定义并不是等于 0 ）

离散点间隔\(T_k = t_{k+1}-t_k\)可以相等也可以不相等。通常取等间隔\(T\)，离散信号可表示为\(f(kT)\)，简写为\(f(k)\)，这种等间隔的离散信号也常称为序列。其中k称为序号

模拟信号、抽样信号、数字信号

通过传感器采集到的很多信号是模拟信号，计算机处理的信号是数字信号

模拟信号：时间和幅值仅为连续的信号，抽样得到抽样信号

抽样信号：时间离散的，幅值连续的信号，量化得到数字信号

数字信号：时间和复制均为离散的信号

连续信号于模拟信号、离散信号与数字信号常通用

周期信号和非周期信号

定义在\((-\infty<t<-\infty)\)区间，每隔一定时间\(T\)（或整数\(N\)）按相同规律重复变化的信号
连续周期信号\(f(t)\)满足：$$ f(t) = f(t+mT), m = 0,\pm1,\pm2,…… $$
离散周期信号\(f(k)\)满足：$$ f(k) = f(k+mN), m = 0,\pm1,\pm2,…… $$
满足以上关系的最小T（或整数N）称为该信号的周期，不具有周期性的信号称为非周期信号（没有规律，并不是不确定性）

能量信号与功率信号

将信号\(f(t)\)施加于 1 电阻上，他所消耗的瞬时功率为\(|f(t)|^2\)，在区间\((-\infty<t<-\infty)\)的能量和平均功率定义为：
(1)信号的能量\(E\)：

\[E^{def} = \int_{-\infty}^{\infty}|f(x)|^2\,dt \]

(2)信号的功率\(P\)：

\[P^{def} = \lim\limits_{T\to\infty}\frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}|f(t)|^2\,dt \]

一维信号和多维信号

一维信号：只有一个自变量描述的信号，如语音信号
多微信号：由多个自变量描述的信号，如图像信号

实信号与复信号

实信号——\(f(t) = f^*(t)\)，它是一个实函数。\(f^*(t)\)为\(f(t)\)的共轭函数
复信号——\(f(t) \neq f^*(t)\)，他是一个复函数，即\(f(t) = f_1(t)+jf_2(t)\)式中的\(f_1(t)\)与\(f_2(t)\)均为实函数

实际信号一般都是实信号，但是为了简化运算，常常引用复信号并以其实部或虚部表示实际信号。例如常用复指数信号：\(e^{jwt} = \cos\omega t + j\sin\omega t\)表示余弦、正弦信号；
常用：$e^{(-\sigma t+j\omega t)} = e^{-\sigma t}\cos\omega t+je^{-\sigma t}\sin\omega t $

几种典型确定性信号

1.指数信号
2.正弦信号
3.复指数信号（表达式具有普遍意义）
4.抽样信号
5.门函数
6.符号信号

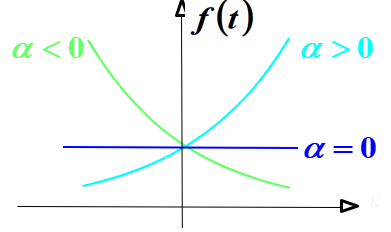
指数信号：\(f(t) = Ke^{\alpha t}\)

\(\alpha = 0\) 直流（常数）

\(\alpha < 0\) 指数衰减

\(\alpha > 0\) 指数增长

图像如下：

单边指数信号：\(f = \begin{cases} 0 & t<0\\ e^{-\frac{t}{\tau}} & t\geq 0 \end{cases}\)

图像如下：

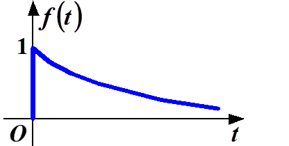
通常把 \(\frac{1}{|\alpha|}\) 称为指数信号的时间常数，记作 \(\tau\) ，代表信号衰减速度，具有时间的量纲
重要特性：其对时间的微分和积分仍然是指数形式

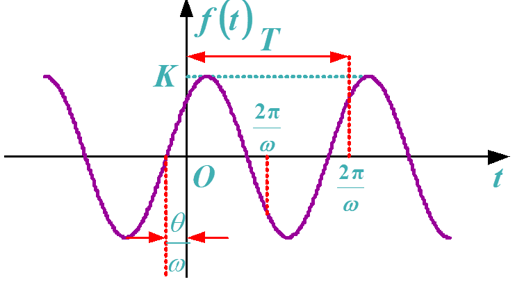
正弦信号：\(f(t) = K\sin (\omega t + \theta)\)

振幅：\(k\)
周期：\(T = \frac{2\pi}{\omega} = \frac{1}{f}\)
频率：\(f\)
角频率：\(\omega = 2\pi f\)
初相：\(\theta\)

衰减正弦信号：

\[f(t) = \begin{cases} Ke^{-\alpha t}\sin(\omega t) & t\geq 0\\ 0 & t<0 \end{cases} \alpha > 0 \]

图像如下：

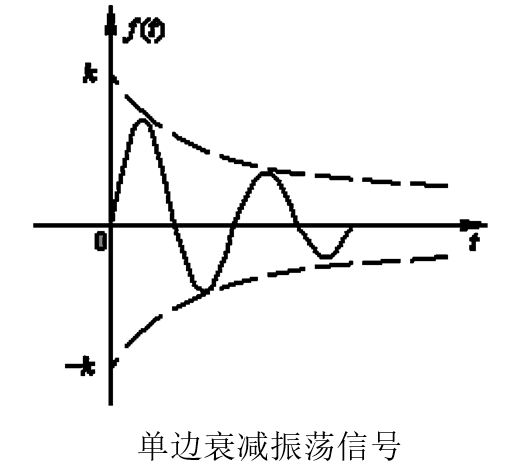
复指数信号：\(f(t) = Ke^{st} (-\infty<t<\infty) = Ke^{\sigma t}\cos(\omega t) + jKe^{\sigma t}\sin(\omega t)\)

\(s = \sigma + j\omega\) 为复数，称为复频率
\(\sigma，\omega\) 均为实数
借用欧拉公式 \(Ke^{st} = Ke^{(\sigma + j\omega)t} = Ke^{\sigma t}e^{j\omega t} = Ke^{\sigma t}\cos(\omega t)+jKe^{\sigma t}\sin(\omega t)\)

\(\sigma\) 表示了正、余弦信号振幅随时间变化的情况；\(\omega\) 是正、余弦信号的角频率

\[ \begin{cases} \sigma = 0, \omega = 0 & 直流\\ \sigma > 0, \omega = 0 & 升指数信号\\ \sigma < 0, \omega = 0 & 衰减指数信号 \end{cases} \ \begin{Bmatrix} \sigma = 0, \omega \neq 0 & 等幅\\ \sigma > 0, \omega \neq 0 & 增幅\\ \sigma < 0, \omega \neq 0 & 衰减 \end{Bmatrix} 震荡 \]

还可以借用欧拉公式将正、 余弦信号表示为复指数形式， 即：

\[\sin\omega t = \frac{1}{2}(e^{j\omega t} - e^{-j\omega t}) \\\\ \cos\omega t = \frac{1}{2}(e^{j\omega t} + e^{-j\omega t}) \]

抽样信号：\(Sa(t) = \frac{\sin t}{t}\)

图像如下：

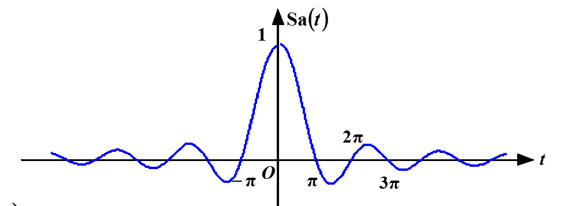
性质：
1.\(Sa(-t) = Sa(t)\)，偶函数
2.\(t = 0,Sa(t)= 1\)，即\(\lim\limits_{t\to 0}Sa(t) = 1\)
3.\(Sa(t) = 0,t = \pm n\pi,n = 1,2,3……\)
4.\(\lim\limits_{t \to \pm \infty}Sa(t) = 0\)

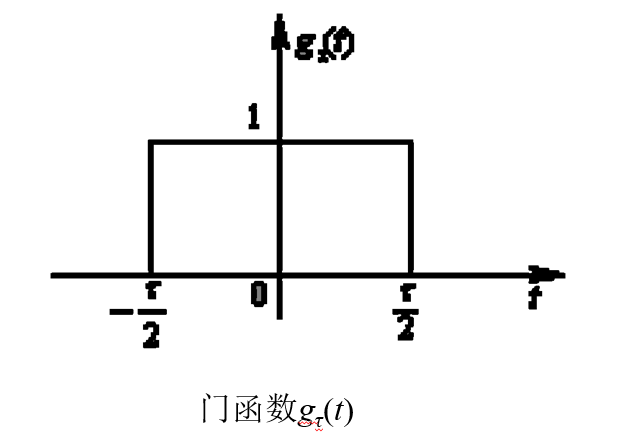
门信号：门函数 \(g_{\tau}(t)\)

门函数 \(g_{\tau}(t)\) 是以原点为中心，以 \(\tau\) 为时宽，幅度为1的矩形单脉冲信号：

\[g_{\tau}(t) = [\varepsilon (t + \frac{\tau}{2}) - \varepsilon (t - \frac{\tau}{2})] = \begin{cases} 1 & |t| < \frac{\tau}{2}\\ 0 & |t| > \frac{\tau}{2} \end{cases} \]

图像如下：

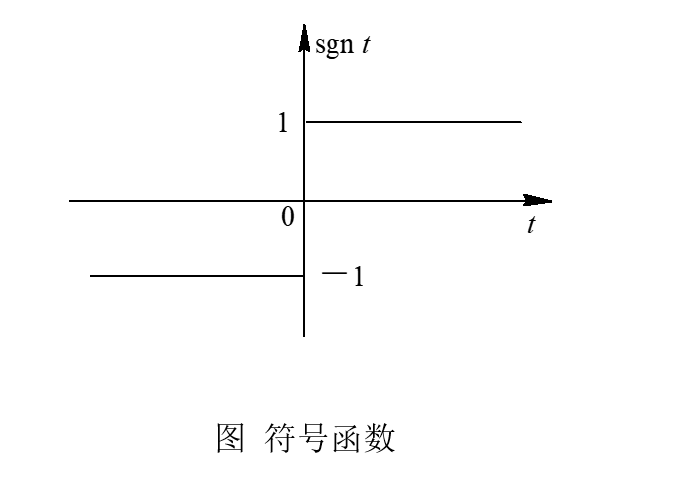
符号信号：符号函数 \(sgn(t)\)

符号函数是 \(t > 0\) 时为 1 ，\(t < 0\) 时为 -1 的函数：

\[sgn(t) = 2\varepsilon(t) - 1 = -\varepsilon(-t) + \varepsilon(t) = \begin{cases} 1 & t > 0\\ -1 & t < 0 \end{cases} \]

图像如下：