七桥问题
七桥问题
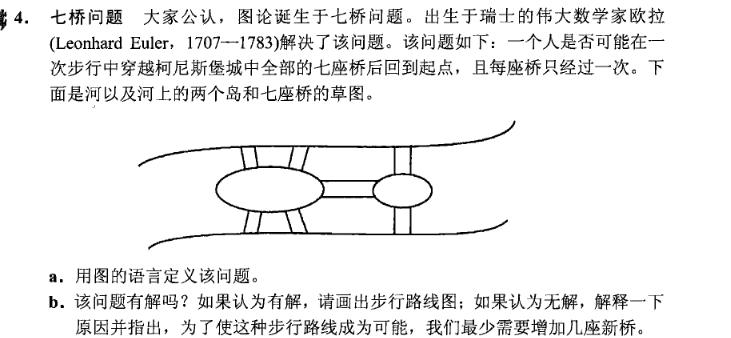
条件:
1.桥只能走一遍,但路可以走多遍,这个条件可以使我们把图简化,也就是说把所有在路上的点看成一个顶点
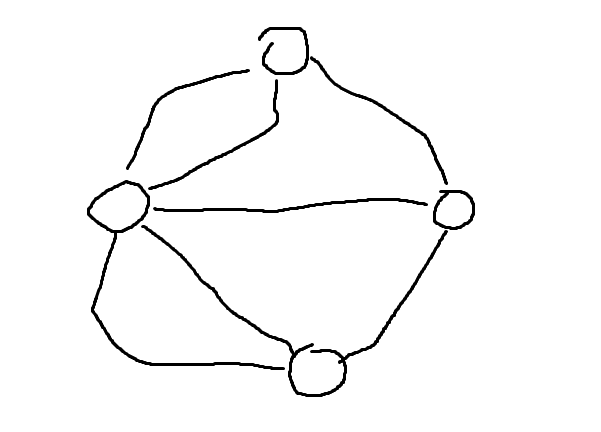
不知道有啥画图软件,本来想用话流程图的画图,但出于懒惰,就直接手画了,抱歉,实在看不下去,可以自己徒手画一下
2.度数为3的有3个,度数为5的有一个(将这个点设为点O),也就是说所有顶点都是度数为奇数的顶点,此外我发现好像还可以简化图,由于上下对称不如把图化简成3个点,也就是1个度数为6的点,1个度数为5的点,和一个度数为3的点。那么我们把这三个点分被称为o1,o2,o3,其中两个奇数点,一个偶数点
3.有三个顶点构成的回路一定会包括o2点到o3点这一条,而且只有这一条。
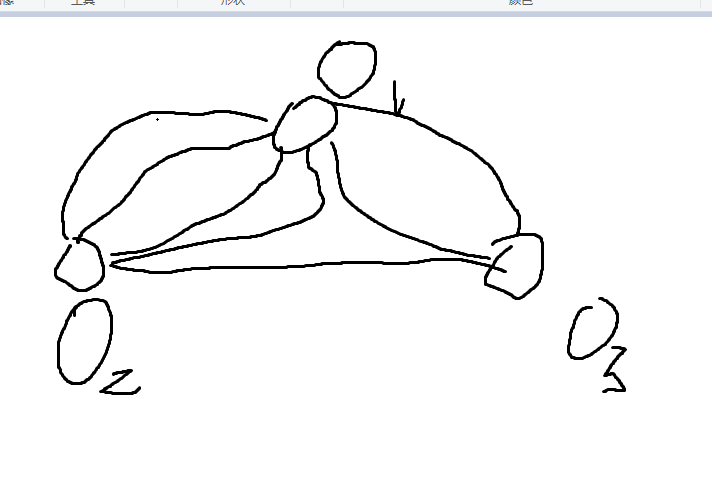
由上我们可以知道,起始点的度数只能是偶数并且必须要和任意点有直接偶数相连(这个可以反证法,为什么间接的不行,找出一个间接相连而不成立的即可,直接相连的一定可以组成回路的),为什么呢?(因为你出去后还要进来,所以肯定是偶数呀)所以起始点只能是o1。
这样后我们可以这样来证明这道题,如果我们从o1出去,并且经过o2和o3在回到起点,我们便把走过的三条边划去,组成新的图,这样我们发现场上全是奇数点,并且任意两点都无法构成回路,所以这道题无解
我明白我这样证明肯定是有很多问题的,希望师傅们能指点我哪里错了。



