几种简单的排序算法(二)基本排序算法
各种排序整理
速查:
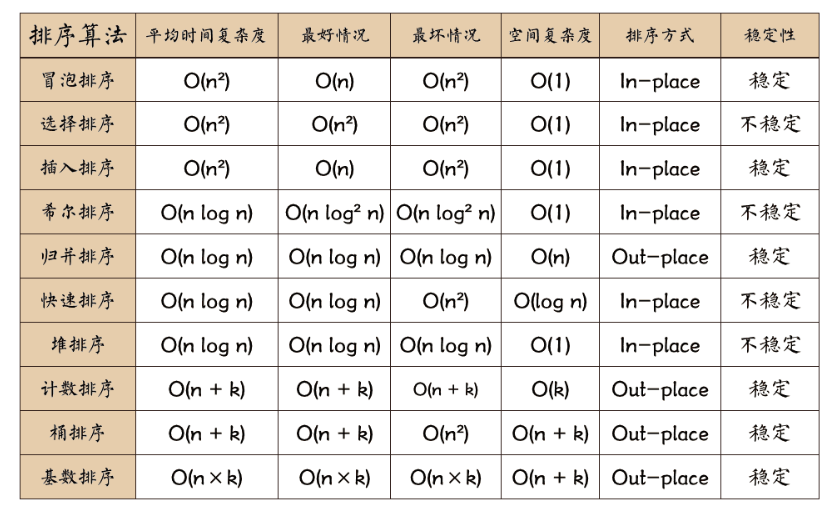
以下的排序用python来实现,比较方便
2、快排
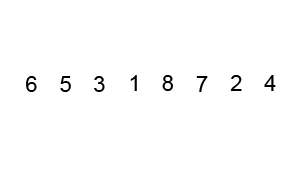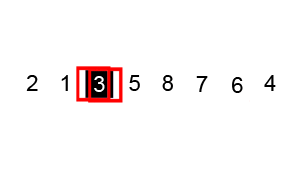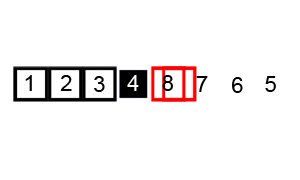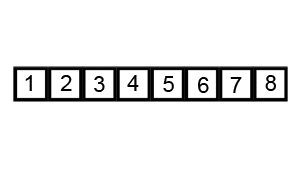
这个图是真的棒!一定要给抄过来哈哈哈哈哈,特地放一下原地址
a)、时间复杂度(重要)
众所周知 快排的 平均时间复杂度 和 最优时间复杂度 都是:O(nlogn),
最坏情况下(元素基本有序):O( n^2 )
b)、概念和实现
快排(quick sort)采用了分治的思想,个人觉得用递归来概括也是可以的。
思想:
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
具体方法:
- 在数列之中,选择一个元素作为”基准”(pivot),或者叫比较值。(一般会选用 左1 元素)
- 数列中所有元素都和这个基准值进行比较,如果比基准值小就移到基准值的左边,如果比基准值大就移到基准值的右边
- 以基准值左右两边的子列作为新数列,不断重复第一步和第二步,直到所有子集只剩下一个元素为止。
代码实现:
def quickSort(targetlist, left ,right):
if left>right:
return
pivot = targetlist[left] # pivot是基准
i = left
j = right
while(i < j):
# 如果right一直大于pivot,则继续走 直到找到比pivot小的
while(targetlist[j] >= pivot and i<j):
j -=1
while(targetlist[i] <= pivot and i<j):
i+=1
# 此时right < pivot,left > pivot, 将i和j做交换
if(i < j): # 这里做判断是为了right到了left位置时,不用再将执行下面这三行代码了
temp = targetlist[i]
targetlist[i] = targetlist[j]
targetlist[j] = temp
# left和right相遇了
# 将相遇点的元素和pivot做交换
targetlist[left] = targetlist[j]
targetlist[j] = pivot
print(targetlist)
# 对于基准点两边的元素分别在做排序
quickSort(targetlist, left,j-1) # 递归
quickSort(targetlist, j+1,right)
if __name__ == "__main__":
target = [180,183,187,182,55,123,490,999,2]
quickSort(target,0,len(target)-1)
print(target)
或者借用lambda表达式 一行代码...也行,下面代码结果是升序的
quick_sort = lambda array: array if len(array) <= 1 else quick_sort([
item for item in array[1:] if item <= array[0]
]) + [array[0]] + quick_sort([item for item in array[1:] if item > array[0]])
target = [180,183,187,182,55,123,490,999,2]
a = quick_sort(target)
print(a)
c)、总结(重要)
- 稳定性:快排是一种不稳定排序,比如基准值的前后都存在与基准值相同的元素,那么相同值就会被放在一边,这样就打乱了之前的相对顺序
- 比较性:因为排序时元素之间需要比较,所以是比较排序
- 时间复杂度:快排的时间复杂度为O(nlogn)
- 空间复杂度:排序时需要另外申请空间(改进算法不需要额外空间),并且随着数列规模增大而增大,其复杂度为:O(nlogn)
- 归并排序与快排 :归并排序与快排两种排序思想都是分而治之,但是它们分解和合并的策略不一样:归并是从中间直接将数列分成两个,而快排是比较后将小的放左边大的放右边,所以在合并的时候归并排序还是需要将两个数列重新再次排序,而快排则是直接合并不再需要排序,所以快排比归并排序更高效一些。
- 快速排序有一个缺点就是对于小规模的数据集性能不是很好。
3、冒泡排序
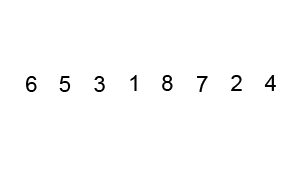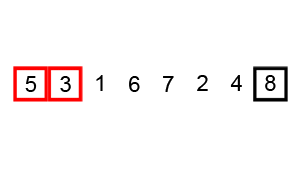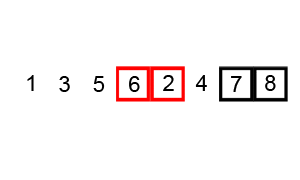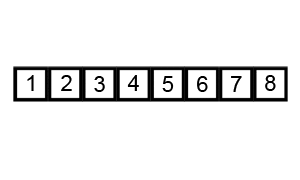
冒泡排序是一种比较容易理解的排序算法,它重复的访问比较要排序的元素列,一次比较两个相邻的元素,一层一层的将较大的元素往后移动,这种类似气泡在上升过程中慢慢变大效果的排序就是冒泡排序
a)、时间复杂度
一般来说,因为它需要双层循环n*(n-1)),所以平均时间复杂度为O(n^2)
改进后的算法这里不考虑。
b)、概念和实现
思想:
- 从第一个和第二个开始比较,如果第一个比第二个大,则交换位置,然后比较第二个和第三个,逐渐往后
- 经过第一轮后最大的元素已经排在最后,所以重复上述操作的话第二大的则会排在倒数第二的位置。
- 那重复上述操作n-1次即可完成排序,因为最后一次只有一个元素所以不需要比较
代码实现:
"""冒泡排序"""
def bubbleSort(targetlist):
# 第一层for循环表示循环的遍数
for i in range(len(targetlist) -1):
# 第二层for表示具体比较哪两个元素
for j in range(len(targetlist) -1 -i):
if targetlist[j] > targetlist[j+1]:
# 如果前大后小,则交换
targetlist[j],targetlist[j+1] = targetlist[j+1],targetlist[j]
if __name__ == "__main__":
target = [180,183,187,182,55,123,490,999,2]
bubbleSort(target)
print(target)
c)、总结
- 这是一种偏慢的排序算法,仅适用于对于含有较少元素的数列进行排序
- 稳定性:只有当前一个元素大于后一个元素时候才会调换顺序,所以它是稳定的
- 比较性:排序时候元素之间需要比较,所以是比较排序
- 空间复杂度:只需要常数个辅助单元,所以空间复杂度为O(1),我们把空间复杂度为O(1)的排序成为原地排序(in-place)
4、选择排序
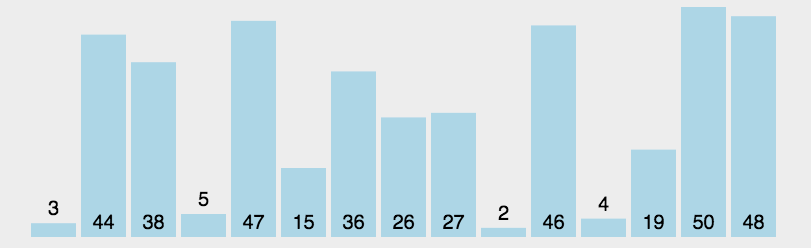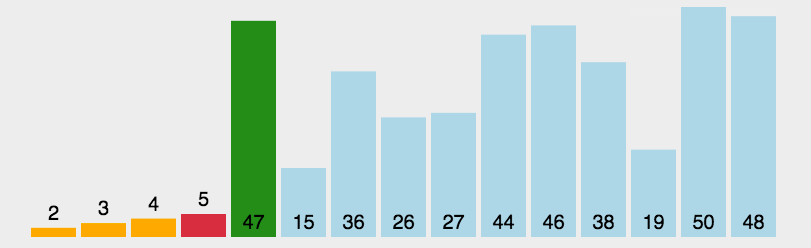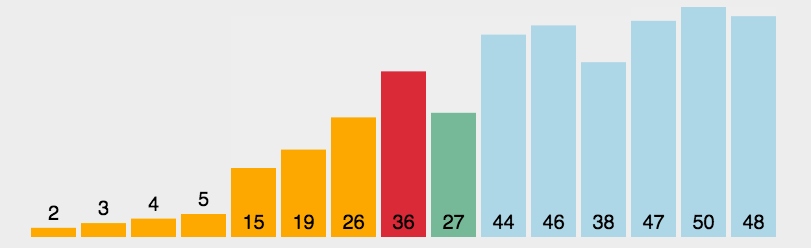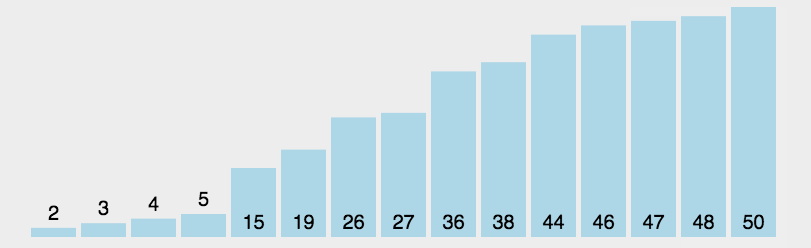
没有找到更好的动图了好可惜
选择排序(selection sort)是一种简单直观的排序算法。每次从待排序的数据元素中选出最小(最大)的一个元素,存放在序列的起始位置,故而称为 选择排序
a)、时间复杂度
选择排序同样是双层循环n*(n-1)),所以时间复杂度也为:O(n^2)
b)、概念和实现
思想:
- 设第一个元素为比较元素,依次和后面的元素比较,比较完所有元素找到最小的元素,将它和第一个元素互换
- 重复上述操作,我们找出第二小的元素和第二个位置的元素互换,以此类推找出剩余最小元素将它换到前面,即完成排序
代码实现:
该实现方法和冒泡方法有点像,都是双层循环
"""选择排序"""
def selectionSsort(targetlist):
# 第一层for表示循环选择的遍数
for i in range(len(targetlist) - 1):
# 将起始元素设为最小元素
min_index = i
# 第二层for表示最小元素和后面的元素逐个比较
for j in range(i + 1, len(targetlist)):
if targetlist[j] < targetlist[min_index]:
# 如果当前元素比最小元素小,则把当前元素角标记为最小元素角标
min_index = j
# 查找一遍后将最小元素与起始元素互换
targetlist[min_index], targetlist[i] = targetlist[i], targetlist[min_index]
if __name__ == "__main__":
target = [180,183,187,182,55,123,490,999,2]
selectionSsort(target)
print(target)
c)、总结
- 稳定性:因为存在任意位置的两个元素交换,比如[5, 8, 5, 2],第一个5会和2交换位置,所以改变了两个5原来的相对顺序,所以为不稳定排序。
- 比较性:因为排序时元素之间需要比较,所以是比较排序
- 空间复杂度:只需要常数个辅助单元,所以空间复杂度也为O(1)
5、插入排序
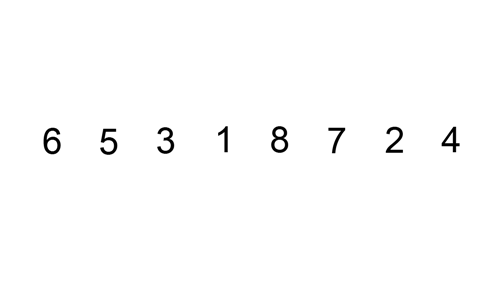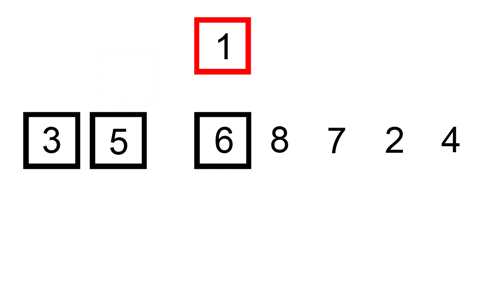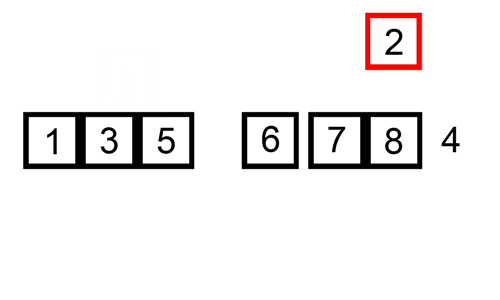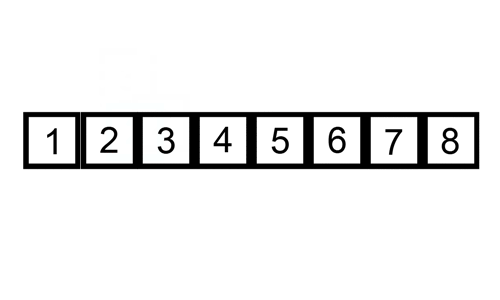
插入排序(Insertion-Sort)的算法描述也是一种简单直观的排序算法。主要时通过构建有序序列,对于未排序的数据,在已排序序列中从后向前扫描,找到相应的位置再插入。就像是在书架中插书:先找到相应位置,将后面的书往后推,再将书插入,如上图所示。
插入排序的适用场景:一个新元素需要插入到一组已经是有序的数组中,或者是一组基本有序的数组排序。
a)、时间复杂度
插入排序同样需要两次循坏一个一个比较,故时间复杂度也为O(n^2)
b)、概念和实现
思想:
- 从第二个元素开始和前面的元素进行比较,如果前面的元素比当前元素大,则将前面元素 后移,当前元素依次往前,直到找到比它小或等于它的元素插入在其后面
- 然后选择第三个元素,重复上述操作,进行插入
- 依次选择到最后一个元素,插入后即完成所有排序
举例:
一次遍历排好一个元素
| 比较次数 | 列表 | 操作 |
|---|---|---|
| 原始序列 | [180,183,187,182,55,123,490,999,2] | |
| 第一次比较后 | [180,183,187,182,55,123,490,999,2] | |
| 第二次比较后 | [180,183,187,182,55,123,490,999,2] | |
| 第三次比较后 | [180,182,183,187,55,123,490,999,2] | 182从后往前同黄色序列比较 |
| 第四次比较后 | [55,180,182,183,187,123,490,999,2] | 55 |
| 第五次比较后 | [55,123,180,182,183,187,490,999,2] | 123 |
| 第六次比较后 | [55,123,180,182,183,187,490,999,2] | |
| 第七次比较后 | [55,123,180,182,183,187,490,999,2] | |
| 第八次比较后 | [2,55,123,180,182,183,187,490,999] | 2 |
代码实现:
"""插入排序"""
def insertionSort(targetlist):
# 第一层for表示循环插入的遍数
for i in range(1, len(targetlist)):
# 设置当前需要插入的元素
current = targetlist[i]
# 与当前元素比较的比较元素
pre_index = i - 1
# 将所有当前元素之前的且大于当前元素的元素向后移动
while pre_index >= 0 and targetlist[pre_index] > current:
# 比较元素大于当前元素则把比较元素后移
targetlist[pre_index + 1] = targetlist[pre_index]
# 向前选择下一个比较元素,继续比较
pre_index -= 1
# 经过上面的一系列挪动,当比较元素小于当前元素,则将当前元素插入在其后面
targetlist[pre_index + 1] = current
if __name__ == "__main__":
target = [180,183,187,182,55,123,490,999,2]
insertionSort(target)
print(target)
c)、总结
-
需要区别于选择排序
-
当一个新元素需要插入到一组已经是有序的数组中,或者是一组基本有序的数组排序(而快排则是基本无序的情况下使用的)
-
其他特点
- 比较性:排序时元素之间需要比较,所以为比较排序
- 稳定性:从代码我们可以看出只有比较元素大于当前元素,比较元素才会往后移动,所以相同元素是不会改变相对顺序是稳定的
- 空间复杂度:只需要常数个辅助单元,所以空间复杂度也为O(1)
还有一些算法后面在更新,今天就先过掉这些基本算法


 浙公网安备 33010602011771号
浙公网安备 33010602011771号